Complete Solutions to Level 1 Subjective of chapter ELECTROMAGNETIC INDUCTION of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | ELECTROMAGNETIC INDUCTION |
| DC PANDEY | Level 1 Subjective |
| Number Of Questions | 21 |
| Academic Year | 2023-24 |
An inductor is connected to a battery through a switch. The emf induced in the inductor is much larger when the switch is opened as compared to the emf induced when the switch is closed. Is this statement true or false?
View SolutionA coil formed by wrapping 50 turns of wire in the shape of a square is positioned in a magnetic field so that the normal to the plane of the coil makes an angle of `30^@`. with the direction of the field. When the magnetic field is increased uniformly from `200 muT` to `600muT` in `0.4 s`, an emf of magnitude 80.0 mV is induced in the coil. What is the total length of the wire?
View SolutionA loop of wire enclosing an area `S` is placed in a region where the magnetic field is perpendicular to the plane. The magnetic field `B` varies with time according to the expression `B=B_0e^(-at)` where a is some constant. That is, at `t= 0`. The field is `B_0` and for `t gt 0`, the field decreases exponentially. Find the induced emf in the loop as a function of time.
View SolutionThe long straight wire in figure (a) carries a constant current `i`. A metal bar of length `i` is moving at constant velocity `v` as shown in figure. Point a is a distance d from the wire.

(a) Calculate the emf induced in the bar.
(b) Which point `a` or `b` is at higher potential?
(c) If the bar is replaced by a rectangular wire loop of resistance `R`, what is the magnitude of current induced in the loop?
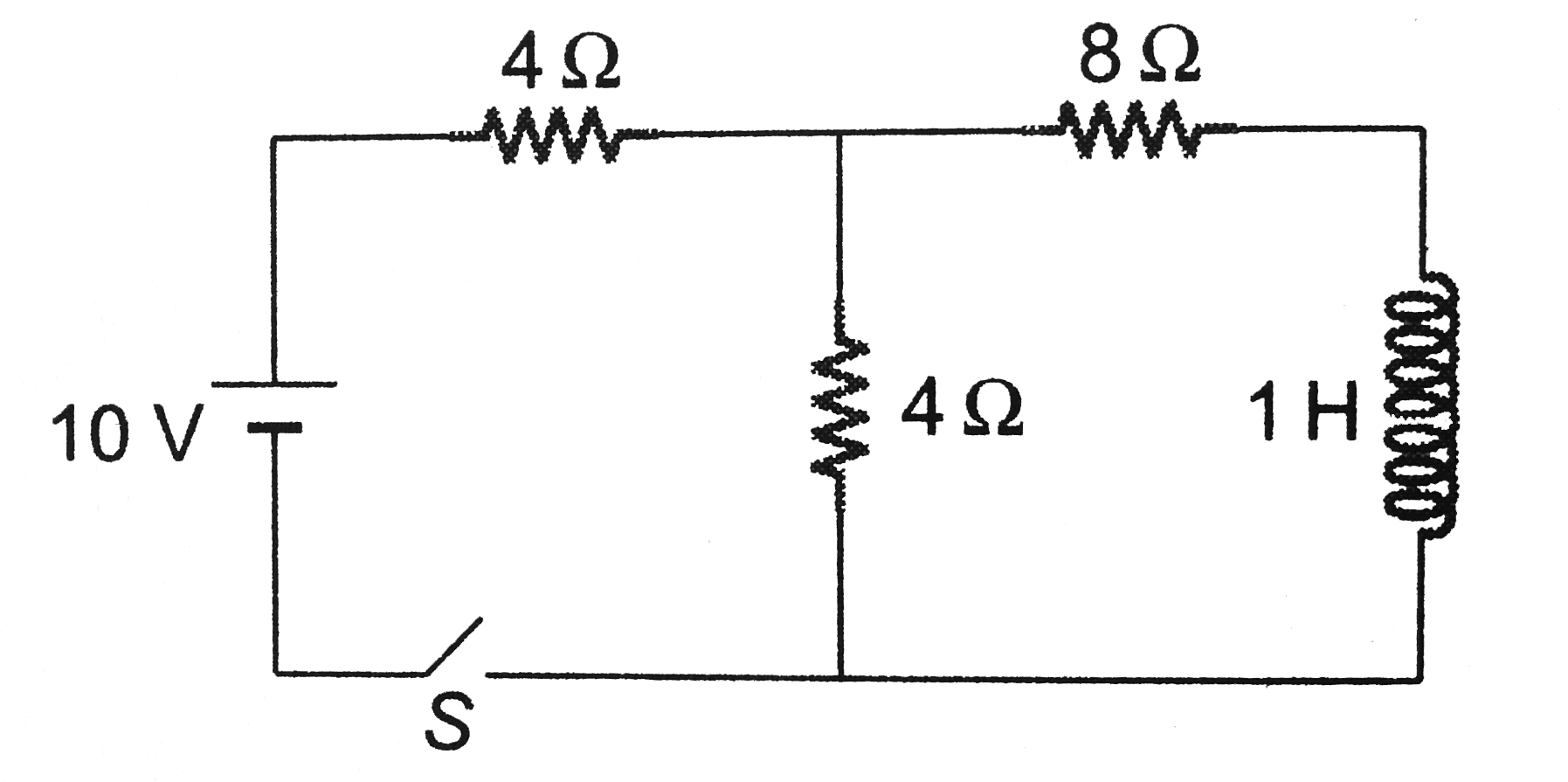
View SolutionThe switch in figure is closed at time `t = 0`. Find the current in the inductor and the current through the switch as functions of time thereafter.
View SolutionA small coil is introduced between the poles of an electromagnet so that its axis coincides with the magnetic field direction. The cross-sectional area of the coil is equal to `S = 3.0 mm^2`, the number of turns is `N = 60`. When the coil turns through `180^@` about its diameter, a galvanometer connected to the coil indicates a charge `q = 4.5muC` flowing through it. Find the magnetic induction magnitude between the poles, provided the total resistance of the electric circuit equals `R = 40 Omega`.
View SolutionThe magnetic field through a single loop of wire, `12 cm` in radius and of `8.5Omega` resistance, changes with time as shown in figure. Calculate the emf in the loop as a function of time. Consider the time intervals
(a) `t = 0` to `t =2.0 s` (b) `t =2.0 s` to `t =4.0 s` (c) `t =4.0 s` to `t =6.0 s`.
The magnetic field is perpendicular to the plane of the loop.

View SolutionA square loop of wire with resistance `R` is moved at constant speed `v` across a uniform magnet field confined to a square region whose sides are twice the lengths of those of the square loop
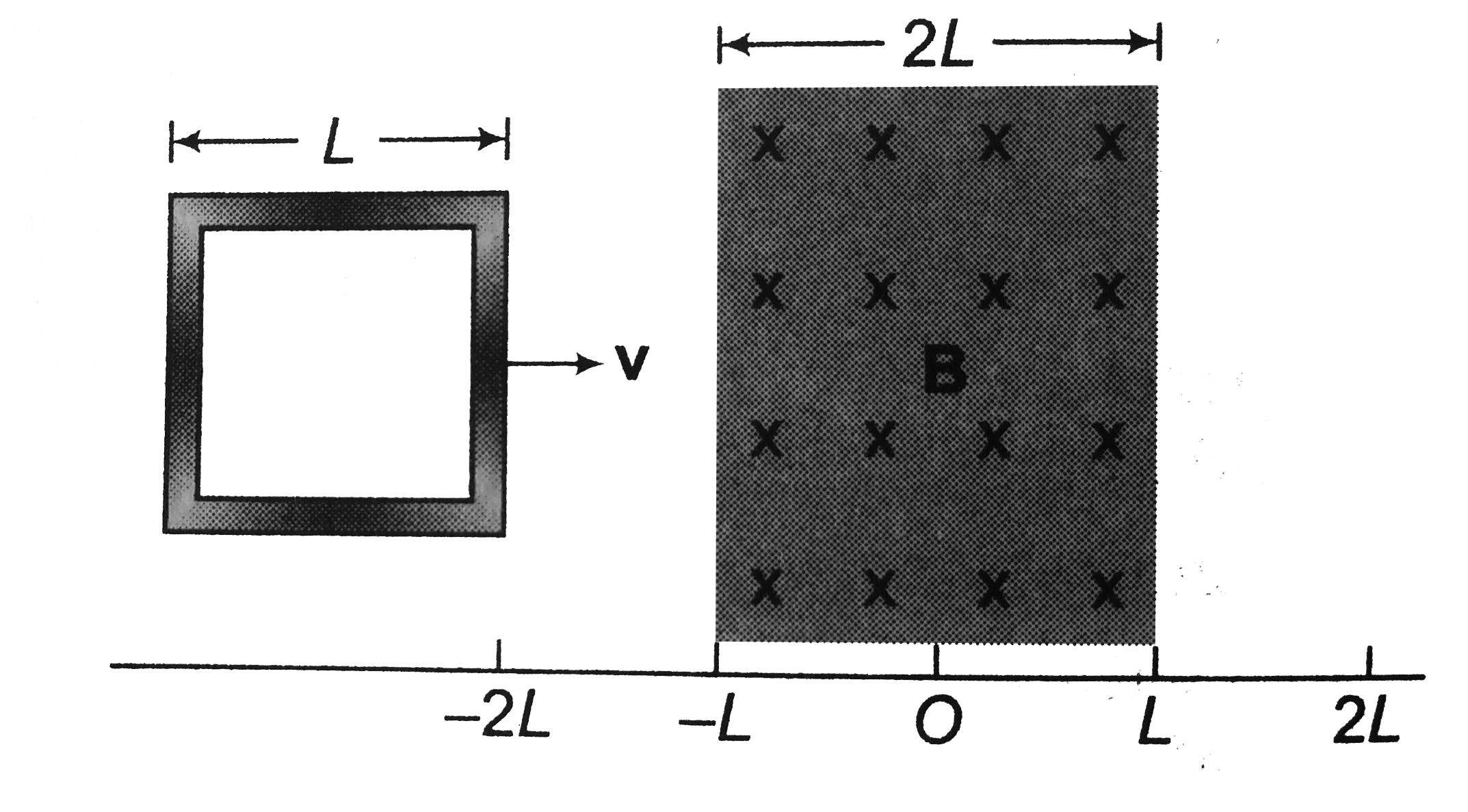
(a) Sketch a graph of the external forces `F` needed to move the loop at constant speed, as a function of to sketch a graph of the external force `F` need tho coordinate `x`, from`x=-2L` to `x=+2L`. (The coordinate `x` is measured from the centre of the oignetic field region to the centre of the loop. It is negative when the centre of the loop is to the left, of the centre of the magnetic field region. Take positive force to be to the right). (b) Sketch a graph of the induced current in the loop as a function of `x`. Take counterclockwise currents to be positive.
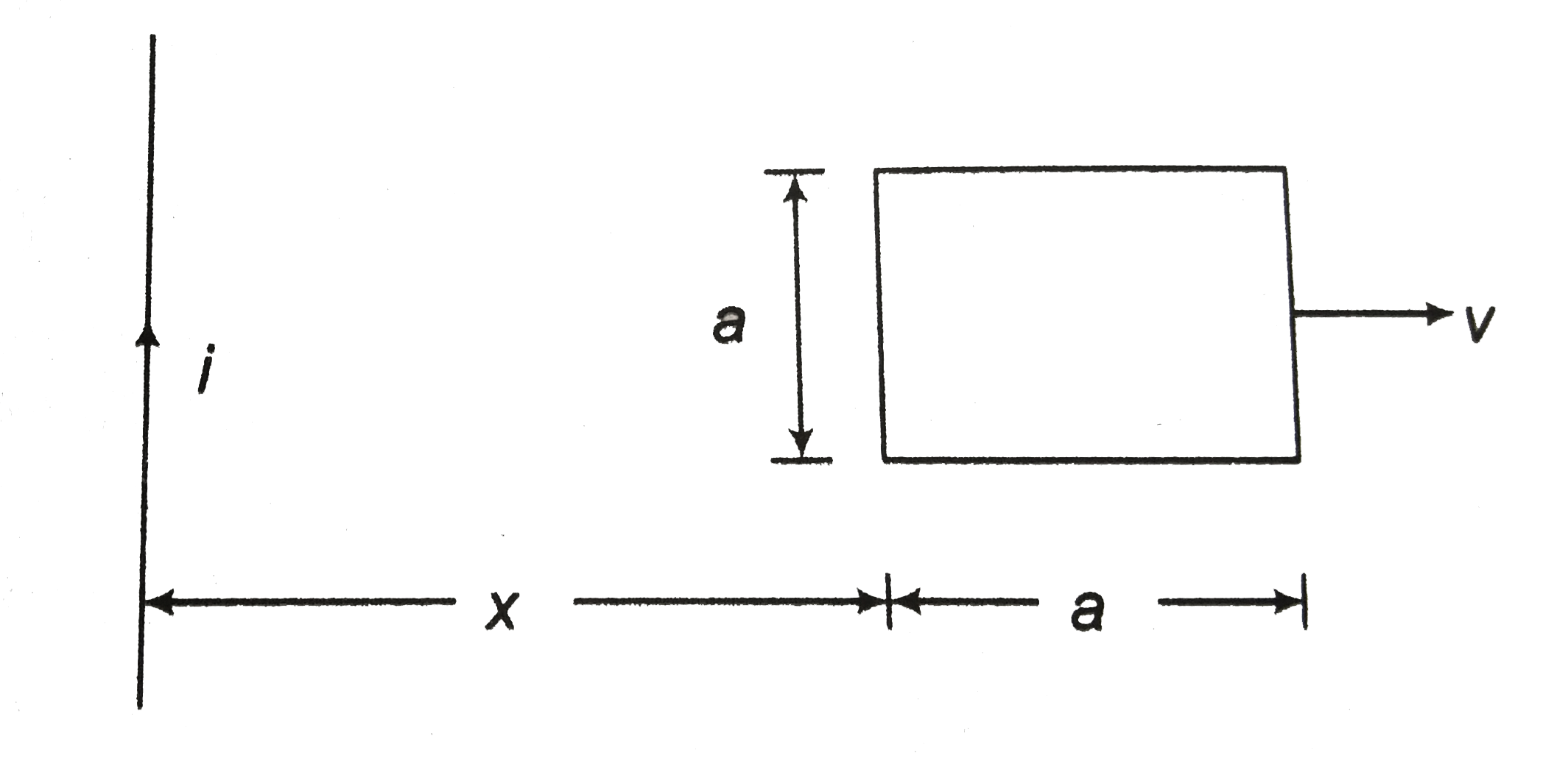
View SolutionA square frame with side a and a long straight wire carrying a current `i` are located in the same plane as m shown in figure. The fram translates to the right with a constant velocity `v`. Find the emf induced in the frame as a function of distance `x`.
View SolutionIn figure, a wire perpendicular to a long straight wire is moving parallel to the later with a speed `v = 10 m//s` in the direction of the current flowing in the later. The current is `10 A`. What is the magnitude of the potential difference between the ends of the moving wire?

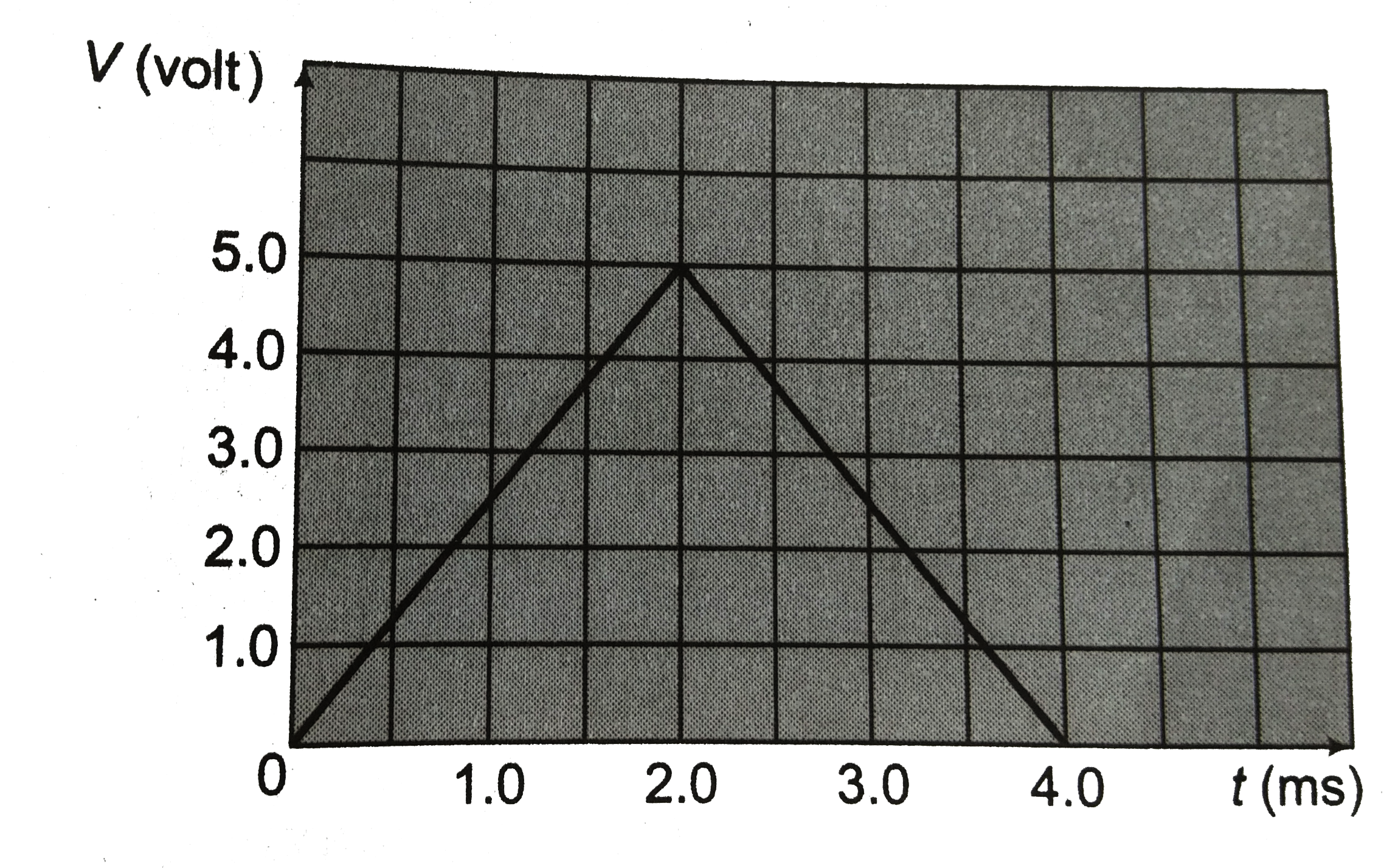
View SolutionThe potential difference across a `150 mH` inductor as a function of time is shown in figure. Assume that the initial value of the current in the inductor is zero. What is the current when `t=2.0 ms`? and `t = 4.0 ms` ?
View SolutionAt the instant when the current in an inductor magnitude of the self-induced emf is `0.0640 A//s`, the magnitude fo the self- induced emf is `0.0160 V`.
(a) What is the inductance of the inductor?
(b) If the inductor is a solenoid with 400 turns, what is the average magnetic flux through each turn when the current is `0.720A`?
View SolutionTwo toroidal solenoids are wound around the same pipe so that the magnetic field of one passes through the turns of the other. Solenoid 1 has 700 turns and solenoid 2 has 400 turns. When the current in solenoid 1 is `6.52 A`, the average flux through each turn of solenoid 2 is `0.0320 Wb`.
(a) What is the mutual inductance of the pair of solenoids?
(b) When the current in solenoid 2 is `2.54 A`, what is the average flux through each solenoid 1?
View SolutionA coil of inductance `1 H` and resistance `10Omega` is connected to a resistanceless battery of emf `50 V` at time `t=0`. Calculate the ratio of rthe rate which magnetic energy is stored in the coil to the rate at which energy is supplied by the battery at `t=0.1s`.
View SolutionA `3.56 H` inductor is placed in series with a `12.8Omega` resistor. An emf of `3.24 V` is then suddenly applied across the `RL` combination.
(a) At `0.278 s` after the emf is applied what is the rate at which energy is being delivered by the battery?
(b) At `0.278 s`, at what rate is energy appearing as thermal energy in the resistor? (c) At` 0.278 s`, at what rate is energy being stored in the magnetic field?
View SolutionA `35.0 V` battery with negligible internal resistance, a `50.0Omega` resistor, and a `1.25 mH` inductor with negligible resistance are all connected in series with an open switch. The switch is suddenly closed
(a) How long after closing the switch will the current through the inductor reach one-half of its maximum value?
(b) How long after closing the switch will the energy stored in the inductor reach one-half of its maximum value?
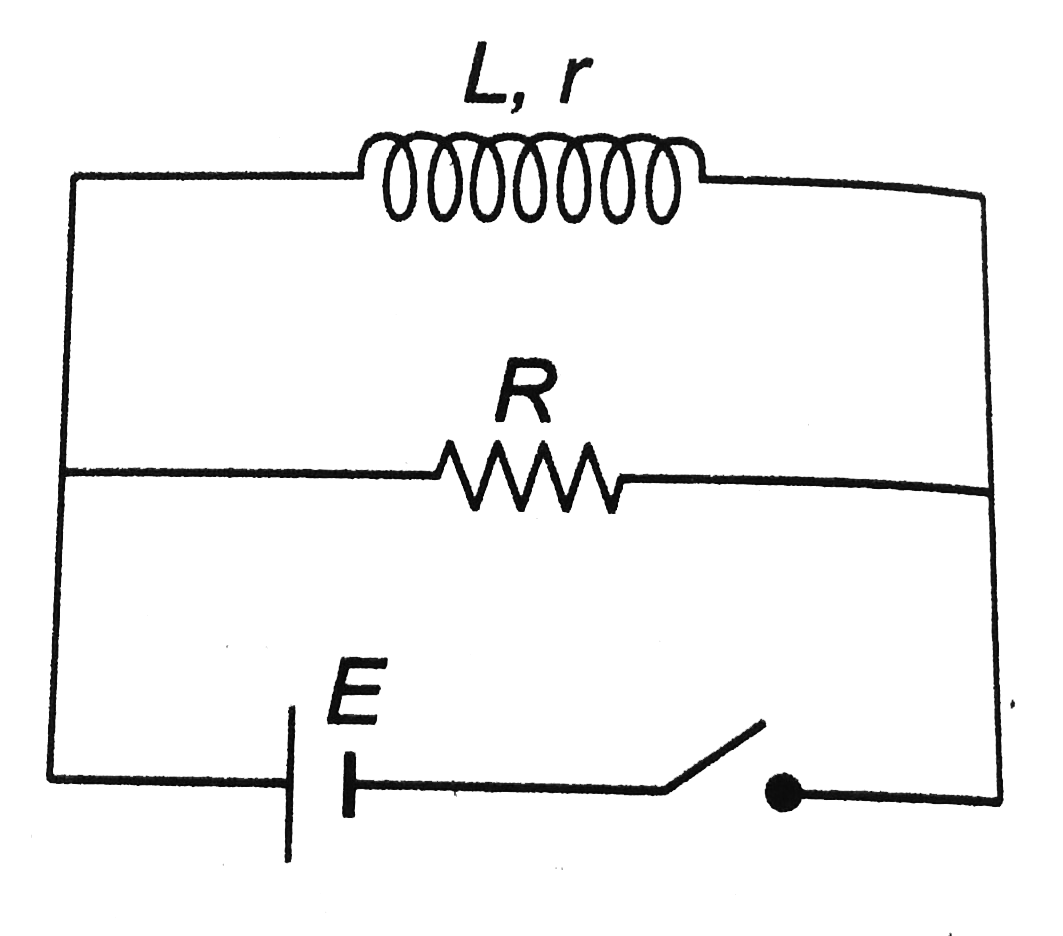
View SolutionA solenoid of inductance `L` with resistance `r` is connected in parallel to a resistance `R`. A battery of emf `E` and of negligible internal resistance is connected across the parallel combination as shown in the figure. At time `t = 0`, switch `S` is opened, calculate
(a) current through the solenoid after the switch is opened.
(b) amount of heat generated in the solenoid.
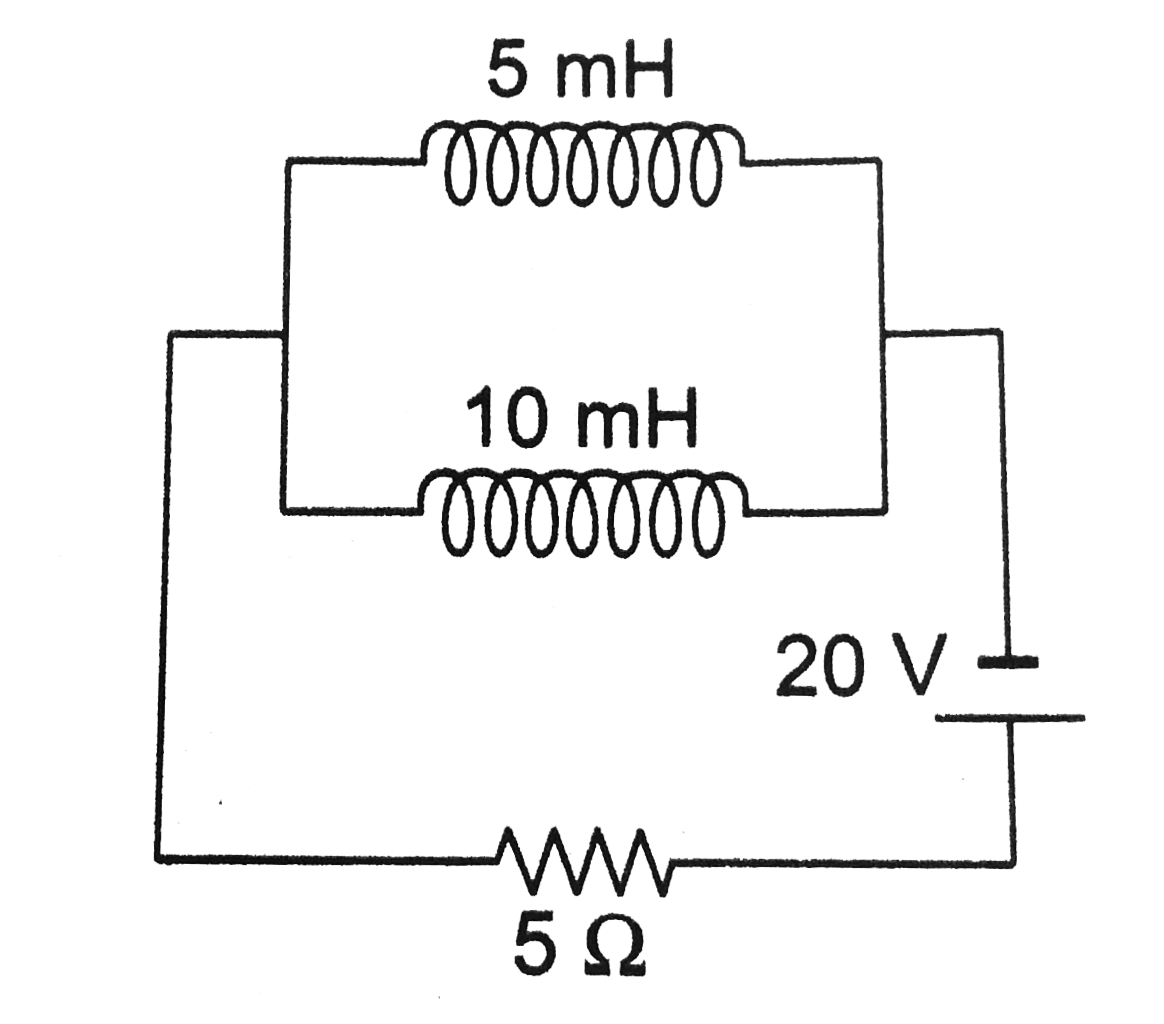
View SolutionIn the given circuit, find the current through the `5 mH` inductor in steady state.
View SolutionIn an oscillating `L-C` circuit in which `C = 4.00muF`, the maximum potential difference capacitor during the oscillations is `1.50 V` and the maximum current through `50.0 mA`.
(a) What is the inductance `L`?
(b) What is the frequency of the oscillations?
(c) How much time does the charge on the capacitor take to rise from zero to its maximum value?
View SolutionIn the `L-C` circuit shown, `C =1muF`. With capacitor charged to `100V`, switch `S` is suddenly closed at time `t = 0`. The circuit then oscillates at `10^3Hz`
(a) Calculate co and T
(b) Express `q` as a function of time
(c) Calculate ``L
(d) Calculate the average current during the first quarter-cycle.
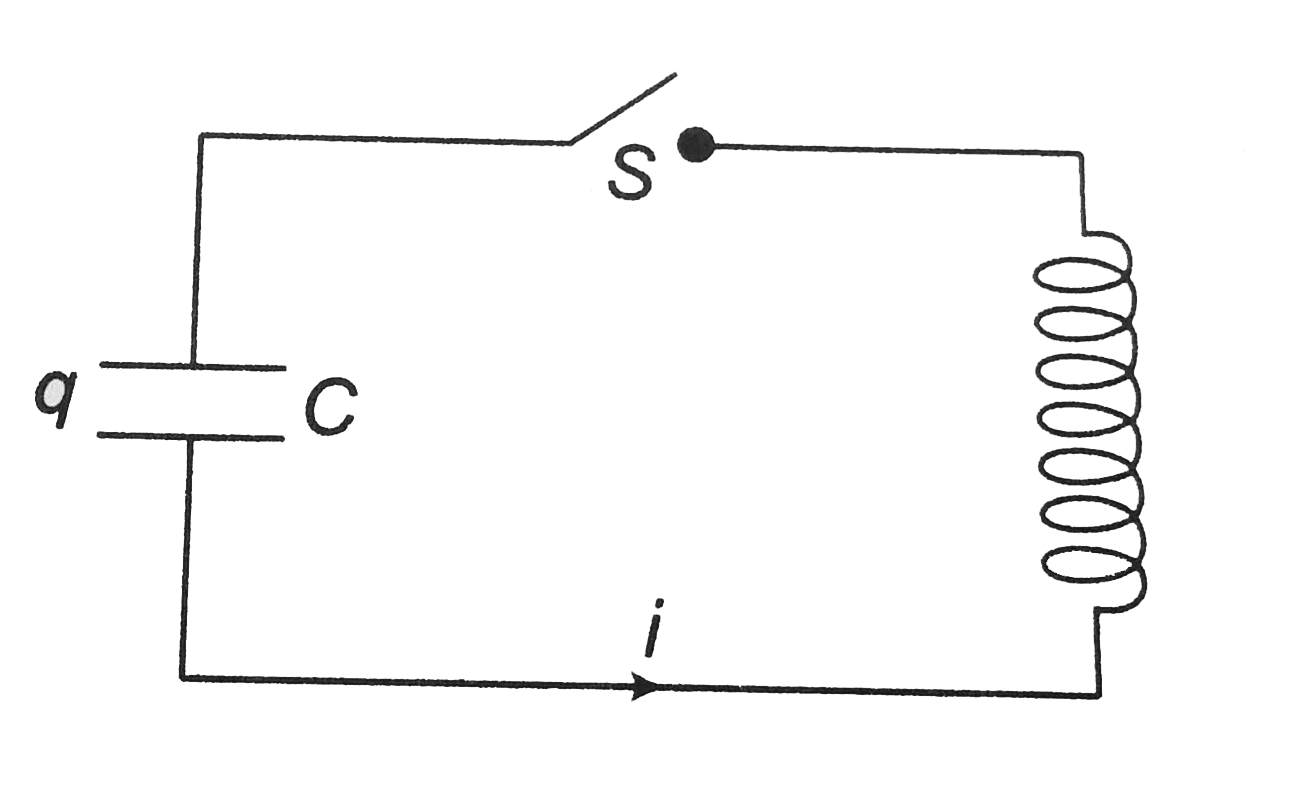
View SolutionAn `L-C` circuit consists of an inductor with `L = 0.0900 H` and a capacitor of `C = 4 x 10-4 F`. The initial charge on the capacitor is `5.00 muC`, and the initial current in the inductor is zero.
(a) What is the maximum voltage across the capacitor?
(b) What is the maximum current in the inductor?
(c) What is the maximum energy stored in the inductor?
(d) When the current in the inductor has half its maximum value, what is the charge on the capacitor and what is the energy stored in the inductor?
View Solution
Level 1 Subjective questions and complete solutions for chapter ELECTROMAGNETIC INDUCTION of DC PANDEY ENGLISH of Class 12
All Exercises from DC PANDEY Class 12 PHYSICS ELECTROMAGNETIC INDUCTION
- Check point
- Example
- Example Type 1
- Example Type 2
- Example Type 3
- Example Type 4
- Example Type 5
- Example Type 6
- Exercise 27.1
- Exercise 27.2
- Exercise 27.3
- Exercise 27.4
- Exercise 27.5
- Exercise 27.6
- Exercise 27.7
- Level 1 Assertion And Reason
- Level 1 Objective
- Level 1 Subjective
- Level 2 Comprehension Based
- Level 2 More Than One Correct
- Level 2 Single Correct
- Level 2 Subjective
- Match the columns
- Medical entrance special format questions
- Medical entrances gallery
- Miscellaneous Examples
- Objective Questions
- SUBJECTIVE TYPE
- Taking it together