Complete Solutions to Critical Thinking (Objective Question) of chapter सरल आवर्त गति of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | सरल आवर्त गति |
| ERRORLESS HINDI | Critical Thinking (Objective Question) |
| Number Of Questions | 51 |
| Academic Year | 2023-24 |
दो कण समान आयाम तथा समान आवृति के साथ एक सीधी रेखा में स. आ. ग. (S.H.M. ) कर रहे है|अब दोनों कण एक दूसरे को पार करके विपरीत दिशा में जाते है तब उनका विस्थापन आयाम का आधा होता है। इन कणों के बीच कलांतर होगा।
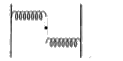
View Solutionलम्बाई L व् द्रव्यमान M की एकसमान छड़ अपने केंद्र पर कीलित है। इस छड़ के सिरों पर k स्प्रिंग नियतांक के एक जैसे स्प्रिंग लगे है जिनके दूसरे सिरे दृढ़ आलम्बों से जुड़े है। छड़ क्षैतिज तल में स्वतंत्र रूप से दोलन कर सकती है। छड़ को एक छोटे कोण ` theta ` से घुमा कर छोड़ दिया जाता है। छड़ के दोलन की आवर्ती होगी।
View Solutionएक बिंदु द्रव्यमान पर दो ज्यावक्रीय विस्थापन `x_1 (t) =A sin omegat ` एवं ` x_2 (t) =A sin ( omega t +(2pi )/( 3)) ` एक साथ x दिशा में लग रहे है। इस द्रव्यमान पर तीसरा ज्यावक्रीय विस्थापन `x_3( t) =B sin ( omega t +phi ) ` लगाने पर वह पूर्ण रूप से रूक जाता है। B तथा `phi` का मान है।
View Solutionm द्रव्यमान का कण x अक्ष पर मूल बिंदु के परितः कम्पन कर रहा है। इसकी स्थितिज ऊर्जा ` U(x) =K[x] ^(3) ` है। यहाँ K एक नियतांक है। यदि दोलन का आयाम a हो तब आवृतकाल T
View Solutionl लम्बाई के एक सरल लोलक का आवृतकाल `T_1` है तथा एक अन्य समान लम्बाई l की एक सिरे पर किलकित और ऊर्ध्वाधर तल में दोलित छड़ का दोलन काल `T_2` है। दोनों ही स्थितियों में दोलनों का आयाम कम है , तब ` (T_1)/( T_2) ` है।
View Solutionदो सरल लोलकों , को जिनकी लम्बाईयाँ 100cm तथा 121 cm है अलग-अलग लटकाया जाता है। इसके बाद उनके गोलकों को खींचकर छोड़ दिया जाता है। लम्बे लोलक के कितने न्यूनतम दोलनों के पश्चात दोनों लोलकों पुनः समान कला में होंगें।
View Solutionसरल आवर्त गति में एक कण का तात्क्षणिक वेग और तात्क्षणिक त्वरण के मध्य कलांतर है।
View Solution200g द्रव्यमान की एक वस्तु को अवमंदन नियतांक ` b= 40 g//s` तथा बल नियतांक `k= 90 N//m` की स्प्रिंग द्वारा सरल आवर्त गति करायी जाती है। तब समय की गणना कीजिए जिसमें आयाम अपने प्रारम्भिक मान से आधा हो जाता है ( दिया है: `ln (1//2) =-0.693) `
View Solution2 मीटर लम्बी एक एकसमान छड़ एक सिरे के द्वारा लटक रही है , तथा यह गुरुत्व के अंतर्गत कम आयाम के दोलन करने के लिए व्यवस्थित है दोलन आवर्तकाल है, लगभग
View Solutionएक कण x - अक्ष के अनुदिश सरल आवर्त गति कर रहा है जिसका आयाम 4 सेमि तथा आवर्तकाल `1.2` सेकंड है , तो कण द्वारा `x= +2` सेमि से ` x=+4` सेमि तक जाने तथा वापस आने में लिए गया न्यूनतम समय है।
View Solutionएक खोखले गोले को उसमें बने हुए एक छिद्र द्वारा पानी से भरा जाता है । तत्पश्चात उसे एक लम्बे धागे द्वारा लटकाकर दोलायमान किया जाता है। जब तल में स्थित छिद्र से पानी धीरे-धीरे बाहर निकलता है , तो गोले का दोलनकाल
View Solution`F_1` बल लगाने पर वस्तु के दोलनों का आवृतकाल ` 4//5` सेकंड है। अन्य बल `F_2` के कारण दोलनों का आवर्तकाल `3//5` सेकंड है। यदि दोनों बल एक साथ लगाए जाएँ तब नया आवर्तकाल होगा।
View Solutionसमान बल नियतांक k वाली तीन स्प्रिंगों A ,B , और C से m द्रव्यमान का एक कण चित्र में दिखाए अनुसार जुड़ा है। यदि कण को स्प्रिंग A के विरूद्ध हल्का सा दबा कर छोड़ा जाए तो दोलनकाल होगा
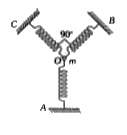
View Solutionएक कण बिंदुओं ` x= -A ` तथा ` x=+A ` के बीच सरल आवर्त गति कर रहा है इसको 0 से `A//2` तक पहुंचने में लगा समय ` T_1` है तथा `A//2 ` से A तक पहुंचने में लगा समय `T_2` है। तब
View Solutionनिम्न में से कौन सा फ़्लन सरल आवर्ती दोलनों को प्रदर्शित करता है
View Solution5 मी तथा 20 मी लम्बाई के दो सरल लोलकों को एक ही दिशा में एक साथ अलप रेखीय विस्थापन दिया जाता है। वे पुनः समान कला में तब होंगें जब छोटा लोलक दोलन पुरे कर लेगा।
View Solutionएक ऊर्ध्वाधर बेलनाकार पात्र में रखी एक आदर्श गैस एक द्रव्यमान M के स्वतंत्र रूप से गतिशील पिस्टन को आधार देती है। पिस्टन और बेलन के अनुप्रस्थ परिच्छेद क्षेत्रफल एकसमान A है। जब पिस्टन साम्यवस्था में है ,तब गैस का आयतन `V_0` है और इसका दाब `P_0` है। पिस्टन को इसी साम्यावस्था स्थिति से थोड़ा सा विस्थापित किया जाता है और फिर छोड़ दिया जाता है। यह मान लें की निकाय अपने परिवेश से पूर्णतः रोधी है तब पिस्टन इस आवर्ती की सरल आवर्त गति करेगा।
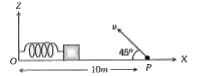
View Solutionएक द्रव्यमान-रहित स्प्रिंग की तनाव -रहित `4.9 m. ` है। उसका एक सिरा बंधित है और दूसरे पर एक छोटा गुटका है (चित्र देखिए) यह निकाय एक घर्षण-रहित क्षैतिज ( horizonatal ) सतह पर रखा है। समय ` t=0` पर गुटके को `2.0` खींचकर स्थिर अवस्था से छोड़ा जाता तब वह गुटका `omega =(pi)/(3) rad//s`आवर्ती का सरल -आवर्त-दोलन करता है। ठीक उसी समय (t =0 ) पर छोटा कंकड़ v चाल से क्षैतिज से `45^(@) ` कोण पर बिंदु P से प्रक्षेपित किया जाता है। बिंदु P की बिंदु O से दुरी ( क्षैतिज) 10m है। यदि t =1s पवार कंकड़ गुटके पर गिरता है, तब v का मान है ` (g= 10m//s^(2) `लें)
View Solutionएक घड़ी जो `20^(@) C ` ताप पर सही समय दर्शाती है इसे `40^(@) C ` ताप पर रखा जाता है। यदि पेंडुलम का रेखीय प्रसार गुणांक `12xx 10 ^(-6) //^(@) C ` हो तो यह कितने समय पीछे या आगे होगी
View Solution`alpha ` कोण पर झुके हुए घर्षण-हिन् नत समतल पर निचे की और गतिमान कार की छत से लटके हुए L लम्बाई के सरल लोलक का आवर्तकाल है
View Solutionकिसी सरल लोलक का गोलक पानी में आवर्तकाल t के साथ सरल आवर्त गति करता है , जबकि इस गोलक के दोलन का वायु में आवर्तकाल `t_(0)` है। पानी का घर्षण बल नगण्य है तथा गोलक का घनत्व `4/3 xx1000" किग्रा/मीटर"^(3)` है। तब निम्नलिखित में से कौन - सा कथन सत्य है -
View Solutionस्प्रिंग स्थिरांक k वाली एक स्प्रिंग को काटकर दो हिस्से इस प्रकार किये जाते है की एक हिस्सा दूसरे से लम्बाई में दुगुना है। तब लम्बे हिस्से का स्प्रिंग स्थिरांक होगा
View SolutionL लम्बाई के धात्विक तार का एक सिरा छत से बंधा गया है तथा दूसरे सिरे पर द्रव्यमानहिन् स्प्रिंग लटकाई गई है। स्प्रिंग का बल नियतांक K है। स्प्रिंग के मुक्त सिरे पर m द्रव्यमान स्वतंत्रता पूर्वक लटक रहा है। तार के अनुप्रस्थ काट का क्षेत्रफल तथा यांग प्रत्यास्थता गुणांक क्रमशा A तथा Y है। यदि द्रव्यमान को थोड़ा सा निचे की और खींचकर छोड़ दिया जाए तो इसके दोलनों का आवर्तकाल होगा
View Solution3 kg द्रव्यमान का एक ठोस सिलिंडर (बेलन) किसी क्षैतिज समतल पर ` 4 ms ^(-1) ` के वेग से लुढ़का रहा है। यह ` 200 Nm^(-1) ` के बल नियतांक के एक क्षैतिज स्प्रिंग ( कमानी) से टकराता है , तो स्प्रिंग से उत्पन्न अधिकतम संपीडन होगा।
View Solutionकमानी स्थिरांक k की किसी कमानी से जुड़े m द्रव्यमान के कण की प्राकृतिक कोणीय आवर्ती `omega _0` है। इस दोलित्र पर कोई ब्रहा बल `F(t)` जो `cos omega t( ( omega ne omega _0) ` के अनुक्रमानुपाती है , आरोपती किया जाता है। इस दोलित्र का समय विस्थापन अनुक्रमानुपाती होगा।
View Solution15 g द्रव्यमान की एक गेंद एक स्प्रिंग वाली बन्दूक से दागी जाती है। स्प्रिंग का स्प्रिंग नियतांक `600N//m` है। यदि स्प्रिंग 5 cm सम्पीड़ित होती है। तो गेंद के द्वारा प्राप्त अधिकतम क्षैतिज प्रेस होगी `( g= 10 m//s ^(2)) `
View SolutionK बल नियतांक वाली एक आदर्श स्प्रिंग को छत से लटकाया गया है एवं M द्रव्यमान का एक गुटका इसके निचले सिरे से जोड़ा गया है। द्रव्यमान M को स्प्रिंग की सामान्य लम्बाई से छोड़ने पर स्प्रिंग में अधिकतम खिंचाव होगा।
View Solutionआवर्त गति करते हुए किसी कण का विस्थापन समीकरण `y= 4 cos ^(2) ((t)/(2)) sin ( 1000 t)` द्वारा प्रदर्शित होता है। यह व्यंजक कितनी स्वतंत्र आवर्त गतियों के अध्यारोपण का परिणाम कहा जा सकता है।
View Solutionकिसी अवमंदित दोलित्र का आयाम 1 मिनट में आधा हो जाता है 3 मिनट बाद इसका आयाम ,मूल आयाम का `(1)/(X) ` गुना हो जाता है , जहाँ X है
View Solutionफलन ` sin ^(2) ( omega t) ` निरूपित करता है
View Solutionकिसी सरल लोलक का प्रारंभिक आवर्तकाल `T_1` है। जब इसका निलंबन बिंदु ऊर्ध्वाधर ऊपर की और समीकरण ` y= kt^(2) ` के anusar गति करता है तो इसका आवर्तकाल `T_2 ` हो जाता है यदि `k= 1m//s^(2) ` हो तो ` (T_1^(2))/( T_2^(2))` का मान होगा `g=10 m//s^(2) ) `
View Solutionकिसी ठोस में चंडी की एक परमाणु `10^(12) //sec` की आवर्ती से किसी दिशा में सरल आवर्त गति करता है। एक परमाणु को दूसरे परमाणु से जोड़ने वाले बंध का बल नियतांक कितना होगा? ( चांदी का आणविक भार =108 और अवागादरी (Avagadro ) =`6.02xxx 10 ^(23) gm" mole " ^(-1)) `
View Solutionचिकनी सतह पर रखे m द्रव्यमान के एक गुटके को स्प्रिंग नियतांक k की एक कमानी (जिसका द्रव्यमान नगण्य है ) से जोड़ा गया है। कमानी का दूसरा सिरा चित्रानुसार, अचल है। आरम्भ में गुटका अपनी साम्यवस्था में स्थायी है। यदि गुटके को एक नियत बल F से खिंचा जाए तो गुटके की अधिकतम चाल होगी।

View Solutionद्रव्यमान m तथा `(m)/(2) ` के दो पिंडों को एक लम्बाई l की द्रव्यमानरहित छड़ के सिरों पर जोड़ा गया है। इस छड़ को एक मरोडांक k के तार से छड़-द्रव्यमान संयोजन के द्रव्यमान केंद्र से चित्रानुसार , लटकाया गया है। मरोडांक k के कारण छड़ के कोणीय विस्थापन `theta` से, उस पर बल आघूर्ण `tau=k theta` लगता है। यदि छड़ को ` theta_0` कोण से घुमा कर छोड़ देते है तो , इसमें तनाव का मान , जब छड़ अपनी माध्य अवस्था से गुजरती है , होगा।
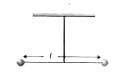
View Solutionद्रव्यमान `'M'` तथा लम्बाई `'2L'` की छड़ को उसके मध्यबिंदु से एक तार द्वारा लटकाया गया है। यह छड़ मरोड़ दोलन करती है। यदि प्रत्येक द्रव्यमान 'm ' के दो पिंडों को छड़ के मध्यबिंदु से `'L//2'` दुरी पर दोनों तरफ जोड़ते है , तो दोलन की आवर्ती `20%` घट जाती है। अनुपात `m//M` का निकटतम मान होगा।
View Solutionएक कण x अक्ष की दिशा में , x =0 के सापेक्ष आयाम A से सरल आवर्त गति कर रहा है। जब इस कण की स्थितिज ऊर्जा तथा गतिज के मान बराबर है , तो कण की स्थिति होगी।
View Solutionएक कण 5 cm आयाम से सरल आवर्त गति कर रहा है। जब कण अपनी माध्य स्थिति से 4 cm दूरी पर है, तब इसके वेग से परिमाण SI मानकों में इसके त्वरण में परिमाण के बराबर है, तो कण का सेकण्ड में आवर्तकाल होगा
View Solutionसरल आवर्त गति करते हुए एक कण का समय पर निर्भर विस्थापन सम्बन्ध `x(t) =A sin ""(pit)/( 90 ) .` से दिया गया है । `t=210s` पर इस कण की गतिज एवं स्थितिज ऊर्जाओं का अनुपात होगा
View Solution1m लम्बाई का एक सरल लोलक कोणीय आवर्ती `10 rad//s` से दोलन कर रहा है । लोलक का आधार ऊपर तथा निचे एक अल्प कोणीय आवर्ती `1 rad//s` से तथा ` 10 ^(-2) m` आयाम से, दोलन आरम्भ करता है। लोलक की कोणीय आवृति में आपेक्षिक परिवर्तन सबसे अच्छा दिया जाता है।
View Solutionएक लोलक सरल आवर्त गति कर रहा है और इसकी अधिकतम गतिज ऊर्जा `K_1` है। यदि लोलक की लम्बाई दोगुनी कर दें और यह पहले समान आयाम से ही सरल आवर्त गति करता है तो इसकी अधिकतम गतिज ऊर्जा `K_2` है। तब
View Solutionएक प्रगामी आवृति तरंग को समीकरण `y(x,y) = 10 ^(-3) sin ( 50 t - 2x ), ` से निरूपित किया जाता है ,जहाँ x तथा y मीटर में तथा t सेकंड में है। निम्न में से तरंग के लिए कौन सा कथन सत्य है।
View Solutionएक सरल लोलक, जो की `l` लम्बाई की डोरी m द्रव्यमान के गोलक से बना है , को एक छोटे कोण `theta _0` से छोड़ा जाता है। यह गोलक एक द्रव्यमान M के गुटके को , जो की क्षैतिज समतल पर रखा है , अपने दोलन के न्यूनतम बिंदु पर प्रत्यास्थ संघट्ट करता है। गोलक संघट्ट कर कोण ` theta _1` तक जाता है। तो M का मान होगा।
View Solutionएक सरल आवर्त गति को निम्न समीकरण से दिखाया जाता है :
` y= 5 ( sin 3pi t +sqrt3 cos pit ) cm`
गति के आयाम तथा आवर्तकाल होंगें।
View Solutionएक ही पदार्थ के एकसमान लम्बाई परन्तु भिन्न त्रिज्या r तथा 2r के दो तारों को जोड़कर , 2L लम्बाई का एक तार बनाया जाता है। यह इस प्रकार कम्पित होता है की दोनों तारों का जोड़ एक निस्पंद बने। यदि तार A में परस्पदों की संख्या P है और B में q है, तब अनुपात `p: q` है।

View Solutionएक अवमंदित आवर्ती दोलक की आवृति प्रति सेकंड 5 दोलन है। इसका आयाम प्रत्येक 10 दोलन के बाद आधा हो जाता है। इसके मूल आयाम को `(1)/( 1000) ` गुना घटाने में लगे समय का सन्निकट मान होगा।
View Solutionएक सरल दोलक का हवा में आवर्तकाल T है। इस दोलक के गोलक को एक श्यानता रहित द्रव , जिसका घनत्व गोलक के घनत्व का `(1)/( 16) ,` है दोलन करवाते है। यदि दोलन के समय यह गोलक पूर्णतया द्रव में रहता है तो इसका आवर्तकाल होगा।
View Solutionएक अवमंदित आवृति दोलक का विस्थापन निम्न है , `x(t) =e^(0.l t) cos (10 pi t +phi) .` यहाँ t सेकंड में है। इसके दोलन आयाम को अपने आरंभिक मान से आधा होने में लगे समय का सन्निकट मान होगा
View Solutionएक स्प्रिंग की स्वतंत्र लम्बाई l तथा बल नियतांक k है। इसे काटकर `l_1` तथा `l_2` स्वतंत्र लम्बाई की दो स्प्रिंगों में बांटते है। `l_1=nl_2` है, जहाँ n एक पूर्णांक है। इनसे सम्बन्ध बल नियतांकों `k_1` तथा `k_2` का अनुपात `k_1//k_2` होगा।
View Solutionसरल आवर्त गति करते किसी कण का विस्थापन `y= A_0 +A sin omegat +B cos omegat ` द्वारा निरूपित किया गया है । तब इसके दोलन का आयाम होगा।
View Solutionएक पूर्ण दोलन में सरल आवर्त गति करते किसी कण का औसत वेग होता है।
View Solutionआरेख में वृत की त्रिज्या , परिक्रमण का आवर्तकाल , आरंभिक स्थिति और परिक्रमण की दिशा प्रदर्शित की गयी है।
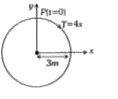
View Solution
Critical Thinking (Objective Question) questions and complete solutions for chapter सरल आवर्त गति of ERRORLESS PHYSICS (HINDI) of Class 12
All Exercises from ERRORLESS HINDI Class 12 PHYSICS सरल आवर्त गति
- Assertion & Reason
- Critical Thinking (Objective Question)
- Graphical Question (Objective Questions )
- JEE Section (Comprehension Type Questions)
- JEE Section (Integer type questions)
- JEE Section (JEE (Advanced )2018)
- JEE Section (Matrix Match Type Questions)
- JEE Section (More than one correct answer)
- JEE Section (Reasoning Type Questions)
- Ordinary Thinking ( Objective Question) (आवर्तकाल एवं आवृति )
- Ordinary Thinking ( Objective Question) (सरल आवर्त गति में ऊर्जा )
- Ordinary Thinking ( Objective Question) (सरल आवर्त गति में कला एवं विस्थापन)
- Ordinary Thinking ( Objective Question) (सरल आवर्त गतियों का अध्यारोपण एवं अनुनाद )
- Ordinary Thinking ( Objective Question) (सरल आवृत गति में त्वरण )
- Ordinary Thinking ( Objective Question) (सरल आवृत गति में वेग )
- Ordinary Thinking ( Objective Question) (सरल लोलक )
- Ordinary Thinking ( Objective Question) (स्प्रिंग लोलक )
- Self Evaluation Test (सरल आवर्त गति )