Complete Solutions to Ordinary Thinking ( Objective Question) (स्प्रिंग लोलक ) of chapter सरल आवर्त गति of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | सरल आवर्त गति |
| ERRORLESS HINDI | Ordinary Thinking ( Objective Question) (स्प्रिंग लोलक ) |
| Number Of Questions | 50 |
| Academic Year | 2023-24 |
बराबर द्रव्यमान के दो पिंड M तथा N दो द्र्व्यमाहीन स्प्रिंगों से अलग-अलग लटके है। स्प्रिंगों के बल नियतांक क्रमशः ` k_1` तथा ` k_2` है। यदि दोनों पिंड उर्ध्वाधर तल में इस प्रकार कम्पन्न करते है की इनके अधिकतम वेग बराबर है , तब म के कम्पन के आयाम का N के साथ अनुपात है।
View Solutionएक द्रव्यमान m , समान लम्बाई की दो स्प्रिंगों से लटका हुआ है। स्प्रिंगों के बल नियतांक क्रमशः `k_1` एवं `k_2` है। जब पिंड का ऊर्ध्वाधर दिशा में दोलन कराया जाता है , तो उसका आवर्तकाल होगा।

View Solutionएक 20g का पिंड K नियतांक की स्प्रिंग से लटकाया गया है। यह ` ( 5)/( pi ) H_2` की आवृति से सरल आवर्त गति करता है। तब स्प्रिंग नियतांक का मान होगा।
View Solution8 kg का पिंड दो हलकी श्रेणीबद्ध स्प्रिंग से चित्रानुसार लटकाया गया है। तब x व् y के पाठ्यांक क्रमशः होंगें।
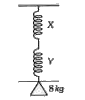
View Solutionचित्र में दिखाया गया द्रव्यमान M सरल आवर्त गति कर रहा है जिसका आयाम A है। बिंदु P का आयाम होगा|

View Solutionएक द्रव्यमान को स्प्रिंग की सहायता से लटकाया गया है जिसका स्प्रिंग नियतांक K है इसे क्षैतिज विस्थापित कर छोड़ दिया जाता है। इस कारण यह T समय के साथ दोलन करने लगता है। लटकाये गए द्रव्यमान का भार होगा (g = गुरुत्वीय त्वरण)
View Solutionएक m द्रव्यमान की वस्तु श्रेणीक्रम में जुड़ी हुए `k_1` एवं `k_2` बल नियतांक की स्प्रिंगों से लटकी हुई है। वस्तु का दोलनकाल होगा।
View Solutionचित्र में चार समान स्प्रिंगों वाले एक सरल आवर्ती दोलित्र का आवर्तकाल है
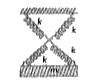
View Solution500g द्रव्यमान के एक गुटके को स्प्रिंग नियतांक `k = 312.5 N//m` की स्प्रिंग से जोड़कर एक घर्षण रहित मेज पर रखा जाता है। स्प्रिंग को दूसरे सिरे पर दृणता से बांध दिया जाता है। गुटके को 5 cm की दुरी एक खिंचा जाता है और सरल आवर्त गति के लिए छोड़ दिया जाता है। इसके दोलन के आवर्तकाल की गणना कीजिए।
View Solutionस्प्रिंग नियतांक K की एक स्प्रिंग पर m द्रव्यमान लटकाया गया है। अब स्प्रिंग को दो बराबर भागों में काटकर किसी एक पर ही द्रव्यमान लटकाया जाता है , तो नया स्प्रिंग नियतांक होगा
View Solution`m_1` और `m_2` दो द्रव्यमान K नियतांक वाली किसी द्रव्यमान विहीन स्प्रिंग से चित्र में दिखाए अनुसार लटके है। संतुलन की अवस्था में, निकाय को प्रभावित न करके यदि `m_1` को धीरे से हटा लिया जाए तो दोलन का आयाम होगा।
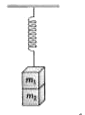
View Solutionएक हल्की स्प्रिंग से M द्रव्यमान लटकाया जाता है। m द्रव्यमान और लटकाने पर इसमें दुरी 'x ' की अतिरिक्त वृद्धि हो जाती है। अब संयुक्त द्रव्यमान का इस स्प्रिंग पर दोलनकाल होगा
View Solutionचित्र में `S_1 ` व `S_2 ` दो रवर्सग स्प्रिंग है। द्रव्यमान m की दोलन आवृति f है। यदि एक स्प्रिंग को हटा दिया जाए तो आवृति हो जायेगी।

View Solutionकिसी तार से लटके हुए हलके स्प्रिंग में 1 किग्रा भार से `9.8` सेमि की उर्ध्वाधर वृद्धि होती है। दोलनकाल होगा
View Solutionतनयहीन लम्बाई L तथा नगण्य द्रव्यमान की एक स्प्रिंग जिसके एक सिरे से कम द्रव्यमान m लटकाया गया है , कोणीय आवर्ती `omega _0` के साथ ऊर्ध्वाधर दोलन कर रही है। जब स्प्रिंग के दूसरे सिरे को स्थाई बिंदु पर रखकर द्रव्यमान को कोणीय गति `omega` के साथ घुमाया जाता है तब द्रव्यमान क्षैतिज समतल में वृतीय पथ पर एक समान गति करने लगता है। इस घूर्णन के दौरान स्प्रिंग की लम्बाई में वृद्धि होगी।
View Solutionजो गुटके में प्रत्येक का द्रव्यमान m है, इन्हें स्प्रिंग नियतांक k की स्प्रिंग से जोड़ा जाता गया है । यदि दोनों को विपरीत दिशाओं में वेग v दिया जाता है तब स्प्रिंग की लम्बाई में अधिकतम वृद्धि होगी।

View Solutionएक क्षैतिज कमानी से बंधा एक द्रव्यमान M आयाम `A_1` से सरल आवर्त गति कर रहा है। जब द्रव्यमान M अपनी माध्य अवस्था से गुजर रहा है , तब एक छोटा द्रव्यमान m इसके ऊपर रख दिया जाता है और अब दोनों आयाम `A_2` से गति करते है। `((A_1)/(A_2))` का अनुपात है
View Solutionएक स्प्रिंग का स्प्रिंग नियतांक `10N//m` है यह स्प्रिंग 10kg द्रव्यमान के साथ सरल आवर्त गति करती है , यदि किसी क्षण पर इसका वेग ` 40 cm //sec` है तो इस स्थिति में इसका विस्थापन होगा( यहाँ आयाम `0.5m ` है )
View Solutionस्प्रिंग के निचले सिरे से एक पिंड लटकाया गया है। पिंड के दोलन का आवर्तकाल 1 से है। यदि इस प्रकार की दो श्रेणीबद्ध स्प्रिंग से पिंड लटकाया जाय तब आवर्तकाल होगा
View Solutionस्प्रिंग नियतांक `8 pi ^(2) N m ^(-1) ` की क्षैतिज स्प्रिंग से एक 500 g का पिंड जुड़ा है । पिंड को उसकी माध्य स्थिति से 10 cm दुरी तक खींचकर छोड़े जाने पर दोलनों की आवर्ती होगी
View Solutionदो स्प्रिंगों के बल नियतांक `K_1` तथा `K_2` है। उन्हें क्रमशः `F_1` तथा `F_2` बलों से इस प्रकार खिंचा जाता है की उनकी प्रत्यास्थ ऊर्जा बराबर हो, तो `F_1,F_2` है ।
View Solutionबल नियतांक ` 800 N m ^(-1) ` की स्प्रिंग से 4kg का द्रव्यमान लटकाया गया है, यह सरल आवृति दोलन करता है। यदि दोलित्र की कुल ऊर्जा 4J हो, तब द्रव्यमान का अधिकतम त्वरण ` (ms^(-2) ` में) होगा।
View Solutionएक गुटका (B ) दो बीना खींची हुई स्प्रिंग `S_1` व `S_2` से जुड़ा है, जिनके स्प्रिंग नियतांक क्रमशः K तथा 4k है ( चित्र -I ) स्प्रिंग के दूसरे सिरे `M_1` तथा `M_1` उपेक्षणीय द्रव्यमान के है। इसमें कही भी घर्षण नहीं है। गुटके B को दीवार -1 की और कम दुरी x से विस्थापित करके छोड़ दिया जाता है ( चित्र-II ) गुटका लोटता है और दीवार -2 की और अधिकतम दूरी y चलता है । गुटके B की साम्य स्थिति के सापेक्ष विस्थापन x और y का मापन किया गया है। अनुपात `(v)/(x) ` होगा।
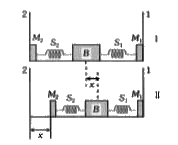
View Solutionदो स्प्रिंग A तथा B के स्प्रिंग नियतांक 2k तथा k है। इन्हें पृथक रूप से समान भार लटकाकर खिंचा जाता है। तब A तथा B को खींचने में सम्पन्न कार्य का अनुपात होगा।
View Solutionस्प्रिंग नियतांक ` K= 200 N//m` की स्प्रिंग का एक सिरा दीवार पर लगाया जाता है। इसे सिरे पर से 10N के बल से लम्बाई के अनुदिश खिंचा जाता है , स्प्रिंग में कितनी वृद्धि होगी।
View Solution`4.9 kg ` द्रव्यमान के एक पिंड को स्प्रिंग से लटकाया गया है तथा यह आवर्तकाल `0.5` सेकंड से दोलन करती है । पिंड को हटाने के पश्चात स्प्रिंग में संकुचन होगा। `( g= 10 ms^(2) ,pi ^(2) =10 ) `
View Solutionचित्र में प्रदर्शित स्प्रिंगों से बने निकाय का परिणामी बल नियतांक होगा।

View Solution40 kg द्रव्यमान की एक मोटर को बल नियतांक ` 4000 Nm^(-1) ` की और चार ऊर्ध्वाधर स्प्रिंग पर चित्रानुसार रखा गया है । मोटर ऊर्ध्वाधर दोलनों का दोलनकाल होगा।
View Solutionस्प्रिंग तुला से 10kg द्रव्यमान को लटकाया गया है। इसे क्षेतिजतः डोरी से एक और इस प्रकार खिंचा जाता है की यह ऊर्ध्वाधर से `60^(@) ` का कोण अंतरित करती है , तुला का इस स्थिति में नया पाठ्यांक होगा।
View Solutionकिसी स्प्रिंग से लटका हुआ m द्रव्यमान 2s में एक दोलन पूर्ण करता है यदि द्रव्यमान में 2 kg की वृद्धि कर दी जाए तो आवर्तकाल में 1s की वृद्धि हो जाती है। द्रव्यमान m है
View Solutionचित्रानुसार एक द्रव्यमान M दो स्प्रिंगों A तथा B से लटकाया गया है। स्प्रिंगों के बल नियतांक क्रमशः `K_1` तथा `K_2` है। दोनों स्प्रिंगों की लम्बाई में कुल वृद्धि है।
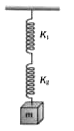
View Solutionचित्र में दिखाई गई स्प्रिंगों के दोलनों की आवृति होगी
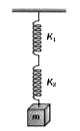
View Solutionएक स्प्रिंग तुला की scale 0 से 10kg तक मापन करती है तथा इसकी लम्बाई ` 0.25 m` है। स्प्रिंग तुला से लटकी हुई एक वस्तु `(pi)/( 10 ) sec` के आवृतकाल से ऊर्ध्वाधर दोलन करती है। लटकी हुई वस्तु का द्रव्यमान होगा, (स्प्रिंग का द्रव्यमान नगण्य है )
View Solutionएक स्प्रिंग का आवृतकाल T है। यदि इसे n समान भागों में तोड़ दिया जाए तो प्रत्येक भाग का आवर्तकाल होगा।
View SolutionK बल नियतांक वाली एक स्प्रिंग का एक-चौथाई भाग काट कर अलग कर दिया जाता है। शेष स्प्रिंग का बल नियतांक होगा
View Solutionएक द्रव्यमान m को `K_1` व `K_2` बल नियतांक वाली दो स्प्रिंगों से अलग-अलग लटकाने पर इनकी सरल आवर्त गतियों के आवृतकाल क्रमशः `t_1` व `t_2` है। यदि उसी द्रव्यमान m को चित्रानुसार दोनों स्प्रिंगों से लटकाया जाये तो इसकी सरल आवर्त गति के आवृतकाल t के लिए सम्बन्ध है

View SolutionK और 2K बल नियतांक की दो स्प्रिन्गे एक द्रव्यमान से चित्रानुसार जुड़ी है। द्रव्यमान के दोलनों की आवृति है

View Solutionएक द्रव्यमान m एक K बल नियतांक तथा l लम्बाई वाली स्प्रिंग से लटकाया गया है। इस द्रव्यमान की दोलन आवृति `f_1` है। यदि स्प्रिंग को दो बराबर भागों में काटकर उसी द्रव्यमान को एक भाग से लटका दिया जाए, तो अब नयी आवर्ती `f_2` है। निम्न में से कोनसा सम्बन्ध सत्य है
View Solutionकिसी कमानी के एक सिरे पर कोई कण आवर्तकाल `t_1` से सरल आवर्त गति करता है, जबकि अन्य कमानी के लिए तदनरूपी आवृतकाल `t_2` है। यदि दोनों कमानियों के श्रेणी संयोजन का आवृतकाल T है , तो
View Solution`k,2k,4k,8k......` स्प्रिंग नियतांक वाली अनंत स्प्रिंगों को श्रेणीक्रम में जोड़ा गया है। संयोजन का प्रभावी स्प्रिंग नियतांक होगा।
View Solutionएक स्प्रिंग दोलक की आवृति दोगुनी करने के लिए हमें
View Solutionनिम्न चित्र में प्रदर्शित दोनों स्प्रिंग एक समान है , यदि `A= 4kg ` स्प्रिंग की लम्बाई में वृद्धि 1 cm है। यदि ` B= 6 kg` है तो इसके द्वारा लम्बाई में वृद्धि होगी
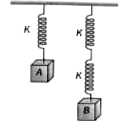
View Solutionजब एक 1kg द्रव्यमान की वस्तु किसी निश्चित हल्की स्प्रिंग से ऊर्ध्वतः लटकाई जाती है ,तो इसकी लम्बाई 5cm बढ़ जाती है यदि स्प्रिंग से 2 kg का गुटका लटककर इसे 10cm तक खींच कर छोड़ दिया जाए तो इसका अधिकतम वेग `(m//s) ` में होगा ( गुरुत्वीय त्वरण = `10m//s^(2) ) `
View Solutionयदि `0.98kg ` द्रव्यमान की एक वस्तु `4.84 N//m,` बल-नियतांक वाली स्प्रिंग पर दोलन करती हो तो वस्तु की कोणीय आवृति है
View Solutionकिसी स्प्रिंग से भार लटकने पर उत्पन्न खिंचाव x हो , तो संचित ऊर्जा का मान होगा ( यदि स्प्रिंग का तनाव T एवं स्प्रिंग नियतांक K हो )
View Solutionएक भार रहित स्प्रिंग जिसकी लम्बाई ` 60 cm `तथा बल नियतांक `100N//m` है, किसी चिकनी मेज पर मुक्त अवस्था में sidhi rakhi है। इसके दोनों सिरे दृढ़तापूर्वक बंधे है। `0.25 kg` द्रव्यमान को स्प्रिंग के madhy में जोड़कर लम्बाई के अनुदिश थोड़ा सा विस्थापित किया जाता है, तो द्रव्यमान का दोलनकाल है
View Solutionभारहीन एक स्प्रिंग का एक सिरा क्षैतिज से जोड़ा गया है तथा इसे ऊर्ध्वाधर रखा है , इसके दूसरे सिरे पर 2 किग्रा के पिंड को पलड़े में रखा गया है (जैसा की चित्र में दर्शया गया है)। स्प्रिंग व पलड़ा भारहीन है। स्प्रिंग नियतांक `200 N//m ` है। इसे जब थोड़ा दबाकर छोड़ा जाता है , तब पिंड सरल आवृत गति करने लगता है। गति का न्यूनतम आयाम कितना होगा चाहिए, जिस पर पिंड पलड़े से पृथक हो जाए ( g = 10 मी/से `""^(2 ) ) `

View Solutionएक हल्की, ऊर्ध्वाधर लटकी स्प्रिंग के निचले सिरे से जुड़ा हुआ कण कम्पन्न कर रहा है। कण का अधिकतम वेग 15 =cm/s है तथा दोलनकाल 628 मिली सेकंड है। गति का आयाम (cm में)
View Solutionकिसी कमानी का upari सिरा स्थिर है तथा निचले सिरे से m द्रव्यमान का एक पिंड लटका है। कमानी का अपना द्रव्यमान नगण्य है । कमानी के निचले सिरे को थोड़ा सा खींचकर छोड़ देने पर द्रव्यमान m का पिंड दोलन करने लगता है और इसके दोलनों का आवृतकाल 3s होता है। m के मान में 1 kg बढ़ाने पर दोलनों का आवृतकाल 5s हो जाता है। m का kg में मान है
View Solutionएक स्प्रिंग (कमानी) का कमानी स्थिरांक k है। इसको तीन भागों में काट दिया गया है जिनकी लम्बाइयों का अनुपात `1:2:3` है। इन तीनों भागों को श्रेणी क्रम में जोड़ने पर संयोजन का कमानी स्थिरांक k तथा समांतर क्रम में जोड़ने पर k " है। तो , अनुपात `k': k''` होगा।
View Solution
Ordinary Thinking ( Objective Question) (स्प्रिंग लोलक ) questions and complete solutions for chapter सरल आवर्त गति of ERRORLESS PHYSICS (HINDI) of Class 12
All Exercises from ERRORLESS HINDI Class 12 PHYSICS सरल आवर्त गति
- Assertion & Reason
- Critical Thinking (Objective Question)
- Graphical Question (Objective Questions )
- JEE Section (Comprehension Type Questions)
- JEE Section (Integer type questions)
- JEE Section (JEE (Advanced )2018)
- JEE Section (Matrix Match Type Questions)
- JEE Section (More than one correct answer)
- JEE Section (Reasoning Type Questions)
- Ordinary Thinking ( Objective Question) (आवर्तकाल एवं आवृति )
- Ordinary Thinking ( Objective Question) (सरल आवर्त गति में ऊर्जा )
- Ordinary Thinking ( Objective Question) (सरल आवर्त गति में कला एवं विस्थापन)
- Ordinary Thinking ( Objective Question) (सरल आवर्त गतियों का अध्यारोपण एवं अनुनाद )
- Ordinary Thinking ( Objective Question) (सरल आवृत गति में त्वरण )
- Ordinary Thinking ( Objective Question) (सरल आवृत गति में वेग )
- Ordinary Thinking ( Objective Question) (सरल लोलक )
- Ordinary Thinking ( Objective Question) (स्प्रिंग लोलक )
- Self Evaluation Test (सरल आवर्त गति )