Complete Solutions to Ordinary Thinking ( Objective Question) (सरल लोलक ) of chapter सरल आवर्त गति of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | सरल आवर्त गति |
| ERRORLESS HINDI | Ordinary Thinking ( Objective Question) (सरल लोलक ) |
| Number Of Questions | 39 |
| Academic Year | 2023-24 |
सरल लोलक का आवृतकाल दुगुना हो जाएगा जबकि
View Solutionअचर लम्बाई के सरल लोलक पृथ्वी की सतह पर आवृतकाल T है। इसका आवर्तकाल खदान के भीतर होगा।
View Solutionस्थिर लिफ्ट में सरल लोलक का आवर्तकाल T है। यदि lift `g//3` त्वरण से ऊपर की और गति करने लगे तो नया आवृतकाल होगा
View Solutionसरल लोलक का आवृतकाल उसकी लम्बाई पर निर्भर करता है
View Solutionकिसी गृह का द्रव्यमान एवं व्यास पृथ्वी का दुगना है , तब इस गृह पर सेकन्डी लोलक का दोलनकाल होगा। (यदि लोलक पृथ्वी पर सेकन्डी लोलक है)
View Solutionएक सरल लोलक को ट्रॉली में रखा जाता है जोकि a त्वरण से एक क्षैतिज सतह पर दायीं और गतिमान है तो मध्य स्थिति में लोलक का धागा ऊर्ध्वाधर से कोण बनाता है।
View Solutionकिसी सरल लोलक का निर्वात में आवृतकाल T है , इसे द्रव गेंद पूर्णतया डूबा देते है। यदि दोलक (bob) का घनत्व द्रव के घनत्व से आठ गुना हो तब आवृतकाल होगा
View Solutionएक मीटर लम्बाई के लोलक को ` 60^(@) ` के कोण से मुफ्त रूप से छोड़ते है। जब इसका कोण ` 30^(@) ` होता है , तो उस समय वेग परिवर्तन की दर होगी। ` (g=10 ` मीटर /से )
View Solutionएक मनुष्य एक स्थिर लिफ्ट के भीतर एक सरल लोलक का काल मापता है तथा T सेकंड प्राप्त करता है। यदि लिफ्ट ऊपर की और ` (g)/(4)` त्वरण के साथ त्वरित होता है , तो लोलक का काल होगा।
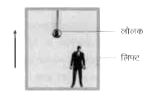
View Solutionएक सरल लोलक को विषुवत रेखा पर ले जाने पर इसका दोलनकाल
View Solutionदो सरल लोलकों की आवृत्ति का अनुपात `2: 3` है, तो उनकी लम्बाइयों का अनुपात होगा।
View Solutionदो लोलक जिनकी लम्बाई `1.44 m ` तथा `1` m है एक साथ दोलन प्रारम्भ करते है। तब दोलनों की संख्या क्या होगी जब वे पुनः एक साथ दोलन आरम्भ करेंगें।
View Solutionनिम्न कथनों में से सही कथन है।
View Solutionयदि सेकंड लोलक की लम्बाई 2 % घटा दी जाए तो प्रतिदिन सेकंडों की हानि है।
View Solutionएक सरल लोलक को दोलनकाल T यदि इसके गोलक को ऋणावेश दिया जाए एवं इसके निचे की सतह को धनावेश दिया जाए तो इसका नया दोलनकाल
View Solutionएक सरल लोलक एक स्थिर एलिवेटर की छत से लटका है तथा इसका दोलनकाल T है। एलिवेटर को गतिमान किया जाता है तथा नया दोलनकाल अधिक प्राप्त होता है|।तब एलिवेटर है।
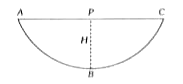
View Solutionm ' द्रव्यमान के गोलक वाला एक सरल लोलक A से C तक दोलन करता है और फिर A पर वापस लोट आता है। PB की दुरी 'H ' है गुरुत्व के कारण त्वरण 'g ' है जब गोलक B से गुजरता है ,तब उसका वेग होगा।
View Solutionनिम्न में से कौन-सा एक सरल आवर्त है
View Solutionसरल लोलक की लम्बाई क्या होगी जहाँ आवर्तकाल 2 सेकंड है ।
View Solutionयदि पृथ्वी के व्यास के अनुदिश खोदी गई सुरंग में एक वस्तु गिराई जाए तो इसकी सरल आवृत गति का दोलन काल होगा।
View Solutionयदि एक सरल दोलक का समय `t=0 s` एवं ` t= tau s,` के बीच एक सार्थक आयाम (अपने मूल आयाम के `1//e` गुणक तक) रहता है तब ` tau ` को दोलक का औसत काल कहा जा सकता है। जब दोलक का गोलीय बॉब अपने वेग के समानुपाती मंदन (श्यान कर्षण के कारण) को सेहता है , जहाँ 'b ' समानुपाती गुणांक है ,तब दोलक का औसत आयुकाल सेकंड में है( यह मान ले की अवमंदन अल्प है)
View Solutionकिसी एक समान तार के अनुप्रस्थ काट के क्षेत्रफल A है। इससे बनाये गए एक लोलक का आवर्तकाल T है। इस लोलक के गोलक से एक अतिरिक्त M द्रव्यमान जोड़ देने से लोलक का आवर्तकाल परिवर्तित होकर ` T_M` हो जाता है। यदि इस तार के पदार्थ का यांग गुणांक Y हो तो `(1)/(Y) ` का मान होगा ( g = गुरुत्वीय त्वरण)
View SolutionL लम्बाई के सरल लोलक का `(g)/(3) ` त्वरण से निचे जाती हुई लिफ्ट में दोलन काल होगा।
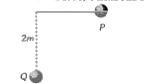
View Solutionजब एक सरल लोलक को चित्र में दिखाए अनुसार P से जोधा जाता है|तो Q तक पहुंचने पर यह वायु घर्षण के कारण कुल ऊर्जा का `10%` भाग खो देता है। Q पर इसका वेग होगा।
View Solutionएक स्थिर लिफ्ट की छत से टंगे हुए सरल लोलक का दोलनकाल T है। यदि parinaami त्वरण `g//4` हो जाता है , तो सरल लोलक का दोलनकाल होगा।
View Solutionएक सरल लोलक का आवृतकाल T है। यदि लोलक की लम्बाई 21 % बढ़ा दी जाए तो इसका आवर्तकाल कितने प्रतिशत बढ़ जाएगा।
View Solutionएक सरल लोलक निर्वात युक्त प्रकोष्ट में दोलन करेगा।
View Solutionसरल लोलक का वेग अधिकतम होगा।
View Solutionनियत त्वरण g से निचे उतरती लिफ्ट में सरल लोलक का आवृतकाल है।
View Solutionएक दोलन करने वाले सरल लोलक का आयाम 10 सेमि तथा आवर्तकाल 4 सेकंड है। अपनी साम्य अवस्था से गुजरने के पश्चात 1 सेकंड के बाद इसकी चाल होगी।
View Solutionकिसी स्थान पर गुरुत्वीय त्वरण ` pi ^(2) m//s^(2) ` हो तब 1 मी लम्बाई वाले सरल लोलक का आवर्तकाल होगा ।
View Solutionएक प्लेट आवर्तकाल T सै दोलन कर रही है। अचानक एक अन्य प्लेट प्रथम प्लेट रख दी जाती है। इसका आवर्तकाल
View Solutionएक स्थिर लिफ्ट की छत सै लटके हुए सरल लोलक का दोलनकाल `T_1` है। जब लिफ्ट नियत वेग सै निचे की और गति करें तो सरल लोलक का दोलनकाल `T_2` हो जाता है, तब
View Solutionयदि एक सरल लोलक की लम्बाई 9 गुना एवं इसके गोलक का द्रव्यमान 4 गुना कर दे तो इसका दोलनकाल हो जायेगा (T = प्रारंभिक दोलनकाल)
View Solutionएक सरल लोलक को यदि पृथ्वी सै चन्द्रमा की सतह पर ले जाकर दोलन कराया जाए तो इसका दोलन काल
View Solutionएक सरल लोलक की लम्बाई l है और इसका अधिकतम कोणीय विस्थापन ` theta` है इसकी अधिकतम गतिज ऊर्जा होगी।
View Solutionएक स्थिर वेन ( गाड़ी) की छत सै लटके हुए सरल लोलक का दोलन काल T है। यदि वेन नियत वेग सै आगे बढे तो सरल लोलक का दोलनकाल हो जाएगा।
View Solutionएक कमरे में एक वस्तु 5 मीटर की दुरी पर स्थित दो दीवारों के लंबवत 20 मी/सेकंड के वेग से चल रही है। घर्षण नहीं और दीवार से संघट्ट प्रत्यास्थ है। वस्तु की गति
View Solutionएक लोलक काफी ऊँचे भवन की छत से लटका है और सरल आवृत दोलक की भाँती मुक्त रूप से आगे-पीछे गति कर रहा है। माध्य स्थिति से 4 m की दुरी पर इसके गोलक का त्वरण `16 m//s^(2) ` है। दोलन का आवर्तकाल है।
View Solution
Ordinary Thinking ( Objective Question) (सरल लोलक ) questions and complete solutions for chapter सरल आवर्त गति of ERRORLESS PHYSICS (HINDI) of Class 12
All Exercises from ERRORLESS HINDI Class 12 PHYSICS सरल आवर्त गति
- Assertion & Reason
- Critical Thinking (Objective Question)
- Graphical Question (Objective Questions )
- JEE Section (Comprehension Type Questions)
- JEE Section (Integer type questions)
- JEE Section (JEE (Advanced )2018)
- JEE Section (Matrix Match Type Questions)
- JEE Section (More than one correct answer)
- JEE Section (Reasoning Type Questions)
- Ordinary Thinking ( Objective Question) (आवर्तकाल एवं आवृति )
- Ordinary Thinking ( Objective Question) (सरल आवर्त गति में ऊर्जा )
- Ordinary Thinking ( Objective Question) (सरल आवर्त गति में कला एवं विस्थापन)
- Ordinary Thinking ( Objective Question) (सरल आवर्त गतियों का अध्यारोपण एवं अनुनाद )
- Ordinary Thinking ( Objective Question) (सरल आवृत गति में त्वरण )
- Ordinary Thinking ( Objective Question) (सरल आवृत गति में वेग )
- Ordinary Thinking ( Objective Question) (सरल लोलक )
- Ordinary Thinking ( Objective Question) (स्प्रिंग लोलक )
- Self Evaluation Test (सरल आवर्त गति )