Complete Solutions to Ordinary Thinking ( Objective Question) (आवर्तकाल एवं आवृति ) of chapter सरल आवर्त गति of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | सरल आवर्त गति |
| ERRORLESS HINDI | Ordinary Thinking ( Objective Question) (आवर्तकाल एवं आवृति ) |
| Number Of Questions | 22 |
| Academic Year | 2023-24 |
कोई कण इस प्रकार गति करता है की उसका त्वरण समीकरण a = -bx द्वारा प्रदर्शित किया जाता है , जिसमें x संतुलन स्थिति से विस्थापन तथा b कोई नियतांक है। दोलनकाल होगा।
View Solutionकिसी कण की गति का समीकरण ` (d^(2)y)/( dt^(2)) +ky =0` है , जहाँ k बल नियतांक है, तो गति का आवर्तकाल होगा।
View Solution
 यदि बालक चित्रानुसार झूले में बैठकर व् खड़े होकर झूलता है , तब दोलन काल में सम्बन्ध है।
यदि बालक चित्रानुसार झूले में बैठकर व् खड़े होकर झूलता है , तब दोलन काल में सम्बन्ध है।
View Solutionसरल आवर्त गति कर रहे किसी कण का आयाम 25 सेमी तथा आवर्तकाल 3 सेकण्ड है | माध्य स्थिति के दोनों ओर इससे 12.5 सेमी दूर स्थिति दो बिंदुओं के बीच गति करने में कण न्यूनतम कितना समय लेगा ?
View Solutionसरल आवर्त गति करने vaale कण की गति समीकरण ` x= 0.01 sin 100 pi (t+0.5 ) ` द्वारा प्रदर्शित होती है, यहाँ पर x मीटर में तथा t सेकंड में है। इस कण का आवर्तकाल होगा।
View Solutionएक कण T आवर्तकाल से सरल आवर्त गति कर रहा है। तो माध्य स्थिति से अधिकतम विस्थापन के आधे तक गति करने में कण द्वारा लिया गया समय होगा।
View Solutionमध्यमान स्थिति से 3 सेमी दुरी पर सरल आवर्त गति करते एक कण का त्वरण 12 सेमी / सेकंड `""^(2 ) ` है। इसका आवर्तकाल है।
View Solutionएक सरल आवर्त गति करते हुए कण का विस्थापन x (मीटर में ) समय t (सेकंड में ) के साथ समीकरण `x= 5 cos ( 4pi t +( pi )/(6))` द्वारा सम्बन्धित है|गति की आवर्ती है।
View Solutionएक कण एक सरल रेखा में सरल आवर्त गति से गतिशील है। यह विरामावस्था से प्रारम्भ कर प्रथम `tau ` सेकंड में दुरी a और अगले ` tau ` सेकंड में दुरी ` 2a` उसी दिशा में तय करता है। तब
View Solutionएक कण एक सरल रेखा में सरल आवृत गति से गतिशील है। यह विरामावस्था से प्रारम्भ कर प्रथम ` tau ` सेकंड में दुरी a और अगले ` tau ` सेकंड में दुरी 2a उसी दिशा में तय करता है। तब
View Solutionएक वस्तु आयाम ` 0.2 m` तथा 24s के साथ सरल आवर्त गति में है। माध्य स्थिति से एक बिंदु `0.1`m की दुरी तक पहुंचने में लगा समय होगा।
View Solutionएक बिंदु सरल आवृत गति कर रहा है जिसका दोलन T है तथा गति का समी`x= a sin (omega t+ pi //6) ` है कितने समय के पश्चात बिंदु का वेग, उसके अधिकतम वेग का आधा होगा।
View Solutionअसत्य कथन है
View Solutionएक कण की सरल आवृत गति को विस्थापन समीकरण `x(t) =A cos (omega t +theta ) ` द्वारा व्यक्त किया जाता है। यदि कण की प्रारंभिक `(t=0) ` स्थिति 1 cm है एवं प्रारंभिक वेग `picm//s` है तब आयाम क्या होगा? कण की कोणीय आवृति `pi s^(-1) ` है।
View Solutionएक कण 4 cm लम्बी रेखा पर सरल आवृत गति कर रहा है जब यह रेखा के मध्य बिंदु से गुजरता है इसका वेग ` 12 cm//s` है कण का आवर्तकाल होगा।
View Solutionसरल आवृत गति करते हुए कण का आयाम a तथा आवृतकाल T है। इसका समीकरण ` y= 5 sin pi ( t+ 4) m` है। मीटर में कण का आयाम (a ) तथा सेकंड में कण का आवर्तकाल (T ) होगा।
View Solution5 cm आयाम की सरल आवृत गति करते एक कण की महत्तम चाल ` 3.14 cm//s` है। इसके कम्पन की आवर्ती है।
View Solutionआयताकार गुटके का द्रव्यमान m एवं अनुप्रस्थकाट A है। घनत्व `rho ` के द्रव में तैर रहा है। इसे माध्य से थोड़ा दबाकर छोड़ने पर यह आवृत काल T से आवृत गति करने लगता है तब
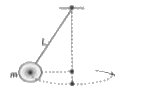
View Solution`0.5 m` लम्बाई (L ) की डोरी के एक sire पर `0.5kg` द्रव्यमान (m ) की गेंद जुड़ी है। यह गेंद क्षैतिज तल में ऊर्ध्वाधर अक्ष के वृतीय घूमती है। डोरी में lag सकने वाला अधिकतम तनाव ` 324 N` है। गेंद का अधिकतम संभावित कोणीय वेग `(radian`/ में ) होगा।
View Solutionएक कण के सरल आवृत्ति दोलन का आयाम a है। इसका दोलन काल T है। माध्य स्थिति से अर्ध आयाम के तुल्य स्थिति तक पहुंचने में लगा न्यूनतम समय होगा :
View Solutionअवमंदित सरल आवर्त गति का समीकरण `m (d^(2) x)/(dt^(2)) +b (dx)/( dt) + kx =0 ` है। दोलनों की कोणीय आवृति होगी
View Solutionधनात्मक `(+ve) x-` दिशा में चलती हुई किसी तरंग का y -दिशा में विस्थापन 1m , तरंगदैध्र्य `2pi m ` है तथा इसकी आवृति `(1)/( pi )Hz` है इस तरंग के लिए सही समीकरण होगा।
View Solution
Ordinary Thinking ( Objective Question) (आवर्तकाल एवं आवृति ) questions and complete solutions for chapter सरल आवर्त गति of ERRORLESS PHYSICS (HINDI) of Class 12
All Exercises from ERRORLESS HINDI Class 12 PHYSICS सरल आवर्त गति
- Assertion & Reason
- Critical Thinking (Objective Question)
- Graphical Question (Objective Questions )
- JEE Section (Comprehension Type Questions)
- JEE Section (Integer type questions)
- JEE Section (JEE (Advanced )2018)
- JEE Section (Matrix Match Type Questions)
- JEE Section (More than one correct answer)
- JEE Section (Reasoning Type Questions)
- Ordinary Thinking ( Objective Question) (आवर्तकाल एवं आवृति )
- Ordinary Thinking ( Objective Question) (सरल आवर्त गति में ऊर्जा )
- Ordinary Thinking ( Objective Question) (सरल आवर्त गति में कला एवं विस्थापन)
- Ordinary Thinking ( Objective Question) (सरल आवर्त गतियों का अध्यारोपण एवं अनुनाद )
- Ordinary Thinking ( Objective Question) (सरल आवृत गति में त्वरण )
- Ordinary Thinking ( Objective Question) (सरल आवृत गति में वेग )
- Ordinary Thinking ( Objective Question) (सरल लोलक )
- Ordinary Thinking ( Objective Question) (स्प्रिंग लोलक )
- Self Evaluation Test (सरल आवर्त गति )