Complete Solutions to JEE Section (Comprehension Type Questions) of chapter सरल आवर्त गति of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | सरल आवर्त गति |
| ERRORLESS HINDI | JEE Section (Comprehension Type Questions) |
| Number Of Questions | 12 |
| Academic Year | 2023-24 |
जब m द्रव्यमान का एक कण :-अक्ष पर V(x) = `kx^(2)`', स्थितिज ऊर्जा से गतिमान होता है, तब यह सरल आवर्त गति करता है। इसका आवर्तकाल `sqrt(m/k)` के समानुपाती होता है, जो कि विमीय विश्लेषण द्वारा आसानी से निकाला जा सकता है। हालाँकि, यदि किसी एक कण की स्थितिज ऊर्जा x = 0 के दोनों तरफ `kx^(2)` से । भिन्न तरह से बढ़े तथा कण की कुल ऊर्जा इतनी हो कि वह अनन्त तक पलायन न कर सके, तब भी कण की गति आवर्ती हो सकती है। m द्रव्यमान का एक कण x-अक्ष पर गति करता है जहाँ । x | के केन्द्र के पास होने पर स्थितिज ऊर्जा V(x) = `ax^(4)`, (a>0) है तथा |x|>`X_(0)` के लिए स्थितिज ऊर्जा V(x) = `V_(0)`, है (चित्र देखें) .
Q |x|> `X_(0)` के लिए कण का त्वरण-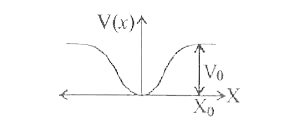
View Solutionजब m द्रव्यमान का एक कण x अक्ष पर `V(x) =kx^(2) ` , स्थितिज ऊर्जा से गतिमान होता है, तब यह सरल आवर्त गति करता है। इसका आवृतकाल `sqrt((m)/(k))` के समानुपाती होता है , जो की विमीय विश्लेषण द्वारा आसानी से निकाला जा सकता है। हालांकि, यदि किसी एक कण की स्थितिज ऊर्जा x =0 के दोनों तरफ `kx^(2) ` से भिन्न तरफ से बढे तथा कण की कुल ऊर्जा इतनी हो की वह अनंत तक पलायन न कर सकें, तब भी कण की गति आवृति हो सकती है। m द्रव्यमान का एक कण x -अक्ष पर गति करता है जहाँ `|x| ` के केंद्र के पास होने पर स्थितिज ऊर्जा ` V(x) =ax^(4),(agt 0 ) ` है तथा `|x| ge X_0` के लिए स्थितिज ऊर्जा `V(x) =V_0` है (चित्र देखें)
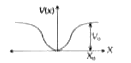
कम आयाम A के दोलन के लिए , कण का आवर्तकाल T निम्न में से किसके समानुपाती है
View Solutionजब m द्रव्यमान का एक कण x अक्ष पर `V(x) =kx^(2) ` , स्थितिज ऊर्जा से गतिमान होता है, तब यह सरल आवर्त गति करता है। इसका आवृतकाल `sqrt((m)/(k))` के समानुपाती होता है , जो की विमीय विश्लेषण द्वारा आसानी से निकाला जा सकता है। हालांकि, यदि किसी एक कण की स्थितिज ऊर्जा x =0 के दोनों तरफ `kx^(2) ` से भिन्न तरफ से बढे तथा कण की कुल ऊर्जा इतनी हो की वह अनंत तक पलायन न कर सकें, तब भी कण की गति आवृति हो सकती है। m द्रव्यमान का एक कण x -अक्ष पर गति करता है जहाँ `|x| ` के केंद्र के पास होने पर स्थितिज ऊर्जा ` V(x) =ax^(4),(agt 0 ) ` है तथा `|x| ge X_0` के लिए स्थितिज ऊर्जा `V(x) =V_0` है (चित्र देखें)
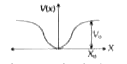
`|x| gt X_0` के लिए कण का त्वरण
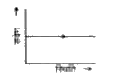
View Solutionहर प्रकार की गतिकीय समस्याओं के विश्लेषण के लिए फेज समष्टि चित्रम ( Phase space diagrams ) का उपयोग किया जाता है। प्रारंभिक दशा, स्थिति व् सवेग में बदलाव होने पर इनका उपयोग चालन में उत्पन्न बदलावों को समझाने में बहुत उपयोगी है। यहाँ हम एक विमीय सरल गतिकीय निकायों की बात करते है । इनके संवेग Y - अक्ष पर रखते है। तब फेज समष्टि चित्राम इस समतल में एक `x(t) vs. p(t) ` (i ) वक्र होता। वक्र पर तीर समय बढ़ाने की दिशा दर्शाता है। उदाहरण के लिए, स्थिर वेग से चल रहें कण के लिए फेज समष्टि चित्राम सरल रेखा है जिसे चित्र में दिखाया गया है। चिन्ह परिपाटी में स्थित या संवेग को ऊपर (या दाहिने ) और धनात्मक तथा निचे (या बायीं) और ऋणात्मक मान जाता है
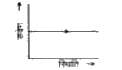
जमीन से ऊपर की और फेंकी गई गेंद का फेज समष्टि चित्राम है।
View Solutionहर प्रकार की गतिकीय समस्याओं के विश्लेषण के लिए फेज समष्टि चित्रम ( Phase space diagrams ) का उपयोग किया जाता है। प्रारंभिक दशा, स्थिति व् सवेग में बदलाव होने पर इनका उपयोग चालन में उत्पन्न बदलावों को समझाने में बहुत उपयोगी है। यहाँ हम एक विमीय सरल गतिकीय निकायों की बात करते है । इनके संवेग Y - अक्ष पर रखते है। तब फेज समष्टि चित्राम इस समतल में एक `x(t) vs. p(t) ` (i ) वक्र होता। वक्र पर तीर समय बढ़ाने की दिशा दर्शाता है। उदाहरण के लिए, स्थिर वेग से चल रहें कण के लिए फेज समष्टि चित्राम सरल रेखा है जिसे चित्र में दिखाया गया है। चिन्ह परिपाटी में स्थित या संवेग को ऊपर (या दाहिने ) और धनात्मक तथा निचे (या बायीं) और ऋणात्मक मान जाता है
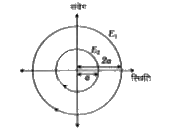
सरल आवर्त दोलन (SHM ) का फेज समष्टि चित्राम उदगम पर केंद्रित वृत है। चित्र में दर्शया गए दो वृत, एक ही दोलक के लिए है, जब उसकी आरंभिक अवस्थाएं भिन्न है ,तथा `E_1` व् `E_2` क्रमशः दोलक की कुल यांत्रिक ऊर्जाएं है। तब
View Solutionएक कण द्रव्यमान m=5 इकाई का एकसमान गति `V=3sqrt2` से रेखा Y=X+4 के अनुदिश XY तल में घूम रहा है । मूलबिन्दु के सापेक्ष इसके कोणीय संवेग का परिमाण
View Solutionद्रव्यमान M तथा त्रिज्या R की एक समान पतली बेलनाकार चक्ति को स्प्रिंग नियतांक k की दो समान द्रव्यमान रहित स्प्रिंग से जोधा जाता गया है जो दीवार पर लगी है ( चित्रानुसार) चकती के एक्सेल से सम्मित रूप में स्प्रिंग चक्ति के केंद्र से दोनों और d दुरी पर जुड़ी है। एक्सेल द्रव्यमान रहित है तथा दोनों स्प्रिंग और एक्सेल क्षैतिज तल में है। प्रत्येक स्प्रिंग की सामान्य स्थिति में लम्बाई L है। प्रारम्भ में चकती दीवार से उसके द्रव्यमान केंद्र (CM ) की दुरी L पर साम्य स्थिति में है। चकती बिना फिसले वेग `V_0=V_0 hati` से लुढ़कती है। घर्षण गुणांक `mu ` है।
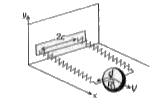
जब चकती का द्रव्यमान केंद्र साम्य स्थिति से x विस्थापन पर होता है, तब इस पर क्रियाशील कुल बाह्य बल होगा।
View Solutionद्रव्यमान M तथा त्रिज्या R की एक समान पतली बेलनाकार चक्ति को स्प्रिंग नियतांक k की दो समान द्रव्यमान रहित स्प्रिंग से जोधा जाता गया है जो दीवार पर लगी है ( चित्रानुसार) चकती के एक्सेल से सम्मित रूप में स्प्रिंग चक्ति के केंद्र से दोनों और d दुरी पर जुड़ी है। एक्सेल द्रव्यमान रहित है तथा दोनों स्प्रिंग और एक्सेल क्षैतिज तल में है। प्रत्येक स्प्रिंग की सामान्य स्थिति में लम्बाई L है। प्रारम्भ में चकती दीवार से उसके द्रव्यमान केंद्र (CM ) की दुरी L पर साम्य स्थिति में है। चकती बिना फिसले वेग `V_0=V_0 hati` से लुढ़कती है। घर्षण गुणांक `mu ` है।
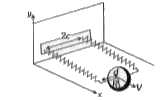
चकती का द्रव्यमान केंद्र, कोणीय आवर्ती `omega` से सरल आवर्त गति करता है , जो बराबर है
View Solutionद्रव्यमान M तथा त्रिज्या R की एक समान पतली बेलनाकार चक्ति को स्प्रिंग नियतांक k की दो समान द्रव्यमान रहित स्प्रिंग से जोधा जाता गया है जो दीवार पर लगी है ( चित्रानुसार) चकती के एक्सेल से सम्मित रूप में स्प्रिंग चक्ति के केंद्र से दोनों और d दुरी पर जुड़ी है। एक्सेल द्रव्यमान रहित है तथा दोनों स्प्रिंग और एक्सेल क्षैतिज तल में है। प्रत्येक स्प्रिंग की सामान्य स्थिति में लम्बाई L है। प्रारम्भ में चकती दीवार से उसके द्रव्यमान केंद्र (CM ) की दुरी L पर साम्य स्थिति में है। चकती बिना फिसले वेग `V_0=V_0 hati` से लुढ़कती है। घर्षण गुणांक `mu ` है।
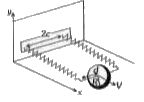
चकती के बिना फिसले लोटनिक गति करने के लिए `V_0` का अधिकतम मान है।
View Solutionसरल आवर्त गति करने वाले एक कण की अधिकतम गति और त्वरण `10 cm s^-1` और `50 cms^-2`। जब गति `8 cm s^-1` हो तो कण की स्थिति ज्ञात कीजिए।
View Solutionसरल आवर्त गति करने वाले एक कण की स्थिति, वेग और त्वरण का परिमाण 2 cm, 1 `ms^-1` और 10 `ms^-2` एक निश्चित क्षण पर पाया जाता है। गति का आयाम और आवर्तकाल ज्ञात कीजिए।
View Solutionसरल आवर्त गति करने वाले कण के लिए त्वरण समानुपाती होता है -
View Solution
JEE Section (Comprehension Type Questions) questions and complete solutions for chapter सरल आवर्त गति of ERRORLESS PHYSICS (HINDI) of Class 12
All Exercises from ERRORLESS HINDI Class 12 PHYSICS सरल आवर्त गति
- Assertion & Reason
- Critical Thinking (Objective Question)
- Graphical Question (Objective Questions )
- JEE Section (Comprehension Type Questions)
- JEE Section (Integer type questions)
- JEE Section (JEE (Advanced )2018)
- JEE Section (Matrix Match Type Questions)
- JEE Section (More than one correct answer)
- JEE Section (Reasoning Type Questions)
- Ordinary Thinking ( Objective Question) (आवर्तकाल एवं आवृति )
- Ordinary Thinking ( Objective Question) (सरल आवर्त गति में ऊर्जा )
- Ordinary Thinking ( Objective Question) (सरल आवर्त गति में कला एवं विस्थापन)
- Ordinary Thinking ( Objective Question) (सरल आवर्त गतियों का अध्यारोपण एवं अनुनाद )
- Ordinary Thinking ( Objective Question) (सरल आवृत गति में त्वरण )
- Ordinary Thinking ( Objective Question) (सरल आवृत गति में वेग )
- Ordinary Thinking ( Objective Question) (सरल लोलक )
- Ordinary Thinking ( Objective Question) (स्प्रिंग लोलक )
- Self Evaluation Test (सरल आवर्त गति )