Complete Solutions to Computing Static Moments and Moments of Inertia. Determining Coordinates of the Centre of Gravity of chapter APPLICATIONS OF THE DEFINITE INTEGRAL of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | APPLICATIONS OF THE DEFINITE INTEGRAL |
| IA MARON | Computing Static Moments and Moments of Inertia. Determining Coordinates of the Centre of Gravity |
| Number Of Questions | 15 |
| Academic Year | 2023-24 |
Find the static moment of the upper portion of the ellipse `(x^(2))/(a^(2)) + (y^(2))/(b^(2))=1` about the x-axis.
View SolutionFind the moment of inertia of a rectangle with base b and altitude h about its base.
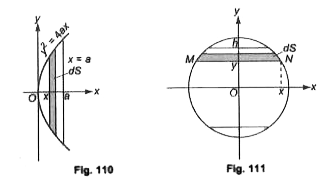
View SolutionCalculate the moment of inertia about the y-axis of the figure bounded by the parabola `y^(2)= 4ax` and the straight line x=a.
View SolutionIn designing wooden girder bridges we often have to deal with logs flattened on two opposite sides. Figure 111. shows the cross-section of such a log. Determine the moment of inertia of this cross-section about the horizontal centre line.
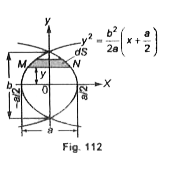
View SolutionFind the moment of inertia about the x-axis of the figure bounded by two parabolas with dimensions indicated in.
View SolutionFind the centre of gravity of the semicircle `x^(2) + y^(2) = a^(2)` situated above the x-axis.
View SolutionFind the coordinates of the centre of gravity of the catenary `y=(1)/(2) (e^(x) + e^(-x))`= cos h x between A(0, 1) and B(a, cosh a).
View SolutionFind the centre of gravity of the first are of the cycloid:
`x=a (t - sin t), y= a (1- cos t) (0 le t le 2pi)`.
View SolutionFind the Cartesian coordinates of the center of gravity of the are of the cardioid `rho = a (1 + cos varphi) " between " varphi = 0 and varphi = pi`.
View SolutionFind the centre of gravity of the figure bounded by the ellipse `4x^(2) + 9y^(2) = 36` and the circle `x^(2) + y^(2) = 9` and situated in the first quadrant
View SolutionFind the Cartesian coordinates of the centre of gravity of the figure enclosed by the curve `= a cos^(3) varphi (a gt 0)`.
View SolutionFind the coordinates of the centre of gravity of the figure bounded by the straight line `y= (2)/(pi)x` and the sinusoid `y = sin x (x ge 0)`
View SolutionUsing the first Guldin theorem, find the centre of gravity of a semicircle of radius a.
View SolutionUsing the second Guldin theorem, find the coordinates of the centre of gravity of the figure bounded by the x-axis and one are of the cycloid: `x=a (t -sin t), y = a (1- cos t)`.
View SolutionAn equilateral triangle with side a revolves about an axis parallel to the base and situated at a distance `b gt a` from the base. Find the volume of the solid of revolution.
View Solution
Computing Static Moments and Moments of Inertia. Determining Coordinates of the Centre of Gravity questions and complete solutions for chapter APPLICATIONS OF THE DEFINITE INTEGRAL of IA MARON MATHS (HINGLISH) of Class 12
All Exercises from IA MARON Class 12 MATHS APPLICATIONS OF THE DEFINITE INTEGRAL
- Area of Surface of Revolution
- Computing Areas in Rectangular Coordinates
- Computing Areas with Parametrically Represented Boundaries
- Computing Pressure, Work and Other Physical Quantities by the Definite Integrals
- Computing Static Moments and Moments of Inertia. Determining Coordinates of the Centre of Gravity
- Computing the Limits of Sums with the Aid
- Computing the Limits of Sums with the Aid Of Definite Integerals
- Computing the Volume of Solid
- Finding Average Values of a Function
- Geometrical Applications of the Definite Integral
- The Arc Length of a Curve in Polar Coordinates
- The Arc Length of a Curve Represented Parametrically
- The Arc Length of a Plane Curve in Rectangular Coordinates
- The Area of a Curvilinear Sector in Polar Coordinates