Complete Solutions to Geometrical Applications of the Definite Integral of chapter APPLICATIONS OF THE DEFINITE INTEGRAL of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | APPLICATIONS OF THE DEFINITE INTEGRAL |
| IA MARON | Geometrical Applications of the Definite Integral |
| Number Of Questions | 10 |
| Academic Year | 2023-24 |
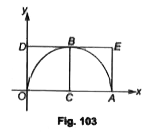
Given: the cycloid `x=a (t- sin t),y = a (1- cos t), 0 le t le 2pi`
Compute. (a) the areas of the surface formed by revolving the arc OBA about the x and y-axis,
(b) the volumes of the solids generated by revolving the figure OBAO about the y-axis and the axis BC,
(c ) the area of the surface generated by revolving the are BA about the axis BC,
(d) the volume of the solid generated by revolving the figure ODBEABO about the tangent line DE touching the figure at the vertex B,
(e ) the area of the surface formed by revolving the are of the cycloid (see item (d)]
View SolutionFind the volume of the solid bounded by the surfaces `z^(2)= 8 (2-x) and x^(2) + y^(2) = 2x`.
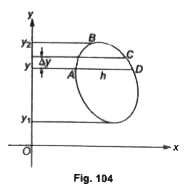
View SolutionProve that if the figure S is bounded by a simple convex contour and is situated between the ordinates `y_(1) and y_(2)`, then the volume of the solid generated by revolving this figure about the x-axis can be expressed by the formula
`V= 2pi int_(y_(1))^(y_(2)) yh dy`,
where `h= x_(2) (y) - x_(1) (y), x= x_(1) (y)` being the equation of the left portion of the contour and `x= x_(2) (y)` that of the right portion.
View SolutionThe planer region bounded by the parabola `y= 2x^(2)+3`, the x-axis and the verticals x=0 and x=1 revolves about the y-axis. Compute the volume of the solid of revolution thus generated.
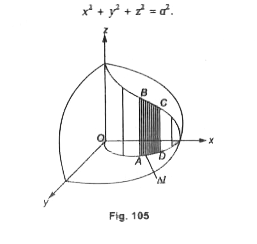
View SolutionCompute the area of the portion of the cylinder surface `x^(2) + y^(2) = ax` situated inside the sphere
`x^(2) + y^(2) + z^(2) = a^(2)`
View SolutionFind the area of the surface out off from a right circular cylinder by a plane passing through the diameter of the base and inclined at an angle of `45^(@)` to the base.
View SolutionThe axes of two circular cylinders with equal bases intersect at right angles. Compute the surface area of the solid constituting the part common to both cylinders.
View SolutionFind the area S of the ellipse given by the equation `Ax^(2) + 2Bxy + Cy^(2) =1 (Delta = AC - B^(2) gt0, C gt 0)`
View SolutionFind the length of the are OA of the curve `y= a "ln" (a^(2))/(a^(2)-x^(2))`, where O(0, 0), `A ((a)/(2), a "ln" (4)/(3))`
View SolutionFind the volume of the solid generated by revolving about the x-axis the figure bounded by the straight lines `y=x +1, y= 2x +1 and x=2`.
View Solution
Geometrical Applications of the Definite Integral questions and complete solutions for chapter APPLICATIONS OF THE DEFINITE INTEGRAL of IA MARON MATHS (HINGLISH) of Class 12
All Exercises from IA MARON Class 12 MATHS APPLICATIONS OF THE DEFINITE INTEGRAL
- Area of Surface of Revolution
- Computing Areas in Rectangular Coordinates
- Computing Areas with Parametrically Represented Boundaries
- Computing Pressure, Work and Other Physical Quantities by the Definite Integrals
- Computing Static Moments and Moments of Inertia. Determining Coordinates of the Centre of Gravity
- Computing the Limits of Sums with the Aid
- Computing the Limits of Sums with the Aid Of Definite Integerals
- Computing the Volume of Solid
- Finding Average Values of a Function
- Geometrical Applications of the Definite Integral
- The Arc Length of a Curve in Polar Coordinates
- The Arc Length of a Curve Represented Parametrically
- The Arc Length of a Plane Curve in Rectangular Coordinates
- The Area of a Curvilinear Sector in Polar Coordinates