Complete Solutions to Computing Areas in Rectangular Coordinates of chapter APPLICATIONS OF THE DEFINITE INTEGRAL of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | APPLICATIONS OF THE DEFINITE INTEGRAL |
| IA MARON | Computing Areas in Rectangular Coordinates |
| Number Of Questions | 25 |
| Academic Year | 2023-24 |
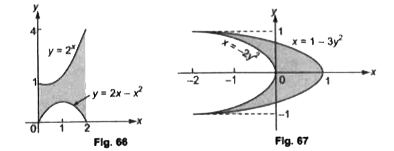
Compute the area of the figure bounded by the straight lines x=0, x=2 and the curves `y= 2^(x), y= 2x- x^(2)`
View SolutionCompute the area of the figure bounded by the parabolas `x= -2y^(2), x= 1-3y^(2)`
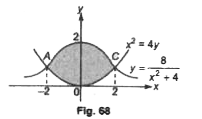
View SolutionFind the area of the figure contained between the parabola `x^(2)= 4y` and the witch of Agnesi `y= (8)/(x^(2)+4)`
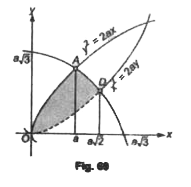
View SolutionCompute the area of the figure which lies in the first quadrant inside the circle `x^(2) + y^(2) = 3a^(2)` and is bounded by the parabolas `x^(2)= 2ay and y^(2) = ax (a gt 0)`
View SolutionCompute the area of the figure lying in the first quadrant and bounded by the curves `y^(2)= 4x, x^(2) = 4y and x^(2) + y^(2) = 5`
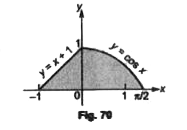
View SolutionCompute the area of the figure bounded by the lines `y= x + 1, y= cos x` and the x-axis
View SolutionFind the area of the segment of the curve `y^(2)= x^(3)-x^(2)` if the line x=2 is the chord determining the segment
View SolutionDetermine the area of the figure bounded by two branches of the curve `(y-x)^(2) = x^(3)` and the straight line x=1
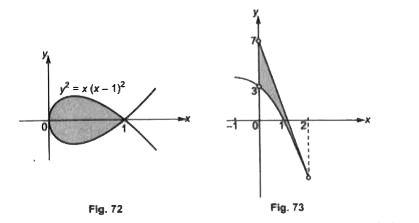
View SolutionCompute the area enclosed by the loop of the curve `y^(2)=x (x-1)^(2)`
View SolutionFind the area enclosed by the loop of the curve `y^(2) = (x-1) (x-2)^(2)`.
View SolutionFind the area of the figure bounded by the parabola `y= -x^(2) + 2x + 3`, the line tangent to it at the point M `(2, -5)` and the y-axis
View SolutionFind the area bounded by the parabola `y= x^(2) -2x + 2`, the line tangent to it at the point M(3,5) and the axis of ordinates
View SolutionWe take on the ellipse
`(x^(2))/(a^(2)) + (y^(2))/(b^(2))=1 (a gt b)`
a point M(x,y) lying in the first quadrant.
Show that the sector of the ellipse bonded by its semi-major axis and the focal radius drawn to the point M has an area.
`S= (ab)/(2) "arc " "cos "(x)/(a)`.
With the aid of this result deduce a formula for computing the area of the entire ellipse.
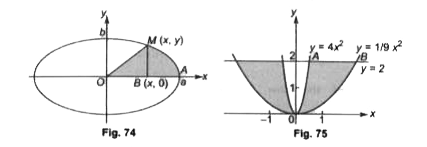
View SolutionThe area bounded between the parabola `x^(2)=y/4` and `x^(2)=9y` and the straight line `y=2` is
View SolutionFrom an arbitrary point M(x,y) of the curve `y= x^(m) (m gt 0)` perpendiculars MN and ML `(x gt 0)` are dropped onto the coordinate axes. What part of the area of the rectangle ONML does the area ONMO constitute ?
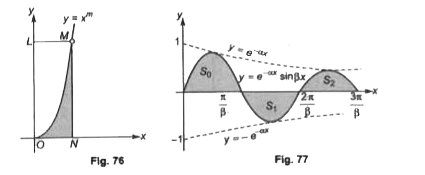
View SolutionProve that the areas `S_(0), S_(1), S_(2), .S_(2),. S_(3)`,….., bounded by the x-axis and half-waves o the curve `y= e^(-alpha x) sin beta x, x ge 0`, from a geometric progression with the common ratio `q=( e^(alpha x)/(beta))`
View SolutionFind the areas enclosed between the circle `x^(2) + y^(2)-2x + 4y-11=0` and the parabola `y= -x^(2) + 2x + 1- 2 sqrt3`
View SolutionFind the area of the region boun ded by curves `f(x)=(x-4)^2,g(x)=16-x^2` andthe x-axis.
View SolutionCompute the area enclosed between the parabolas
`x= y^(2), x= (3)/(4) y^(2)+1`
View SolutionCompute the area enclosed by the curve `y^(2)= (1-x^(2))^(3)`
View SolutionCompute the area enclosed by the loop of the curve `4(y^(2)-x^(2))+ x^(3)=0`
View SolutionCompute the area of the figure bounded by the curve `sqrtx + sqrty=1` and the straight line `x+ y =1`
View SolutionCompute the area of the figure enclosed by the curve `y^(2) =x^(2) (1-x^(2))`
View SolutionCompute the area enclosed by the loop of the curve `x^(3) + x^(2) - y^(2) = 0`
View SolutionCompute the area bounded by the axis of ordinates and the curve `x= y^(2) (1-y)`
View Solution
Computing Areas in Rectangular Coordinates questions and complete solutions for chapter APPLICATIONS OF THE DEFINITE INTEGRAL of IA MARON MATHS (HINGLISH) of Class 12
All Exercises from IA MARON Class 12 MATHS APPLICATIONS OF THE DEFINITE INTEGRAL
- Area of Surface of Revolution
- Computing Areas in Rectangular Coordinates
- Computing Areas with Parametrically Represented Boundaries
- Computing Pressure, Work and Other Physical Quantities by the Definite Integrals
- Computing Static Moments and Moments of Inertia. Determining Coordinates of the Centre of Gravity
- Computing the Limits of Sums with the Aid
- Computing the Limits of Sums with the Aid Of Definite Integerals
- Computing the Volume of Solid
- Finding Average Values of a Function
- Geometrical Applications of the Definite Integral
- The Arc Length of a Curve in Polar Coordinates
- The Arc Length of a Curve Represented Parametrically
- The Arc Length of a Plane Curve in Rectangular Coordinates
- The Area of a Curvilinear Sector in Polar Coordinates