Complete Solutions to Computing the Volume of Solid of chapter APPLICATIONS OF THE DEFINITE INTEGRAL of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | APPLICATIONS OF THE DEFINITE INTEGRAL |
| IA MARON | Computing the Volume of Solid |
| Number Of Questions | 10 |
| Academic Year | 2023-24 |
Find the volume of the ellipsoid `(x^(2))/(a^(2)) + (y^(2))/(b^(2)) + (z^(2))/(c^(2))=1`
View SolutionThe axes of two identical cylinders with bases of radius a intersect at right angles. Find the volume of the solid constituting the common portion of the two cylinders.
View SolutionOn all chords (parallel to one and the same direction) a circle of radius R symmetrical parabolic segments of the same altitude h are constructed. The planes of the segments are perpendicular to the plane of the circle. Find the volume of the solid thus obtained
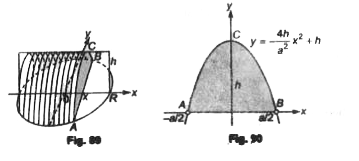
View SolutionCompute the volume of the solid generated by revolving about the x-axis the area bounded by the axes of coordinates and the parabola `x^((1)/(2)) +y^((1)/(2)) = a^((1)/(2))`.
View SolutionThe figure bounded by an arc of the sinusoid y= sin x, the axis of ordinates and the straight line y=1 resolves about the y-axis
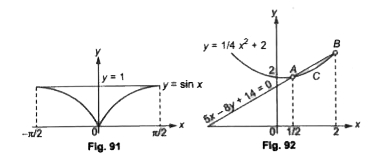
Compute the volume V of the solid of revolution thus generated.
View SolutionCompute the volume of the solid generated by revolving about the x-axis the figure bounded by the parabola `y= 0.25 x^(2) + 2` and the straight line `5x -8y + 14=0`
View SolutionCompute the volume of the solid generated by revolving about the y-axis the figure bounded by the parabolas `y= x^(2) and 8x= y^(2)`
View SolutionFind the volume of the solid generated by revolving about the line `y= -2a` the figure bounded by the parabola `y^(2)= 4ax` and the straight line x=a

View SolutionFind the volume of the solid generated by revolving about the x-axis the figure enclosed by the astroid : `x= a cos^(3)t , y= a sin^(3)t`.
View SolutionCompute the volume of the solid obtained by revolving about the polar axis the cardioid `rho = a (1 + cos varphi)` shown in
View Solution
Computing the Volume of Solid questions and complete solutions for chapter APPLICATIONS OF THE DEFINITE INTEGRAL of IA MARON MATHS (HINGLISH) of Class 12
All Exercises from IA MARON Class 12 MATHS APPLICATIONS OF THE DEFINITE INTEGRAL
- Area of Surface of Revolution
- Computing Areas in Rectangular Coordinates
- Computing Areas with Parametrically Represented Boundaries
- Computing Pressure, Work and Other Physical Quantities by the Definite Integrals
- Computing Static Moments and Moments of Inertia. Determining Coordinates of the Centre of Gravity
- Computing the Limits of Sums with the Aid
- Computing the Limits of Sums with the Aid Of Definite Integerals
- Computing the Volume of Solid
- Finding Average Values of a Function
- Geometrical Applications of the Definite Integral
- The Arc Length of a Curve in Polar Coordinates
- The Arc Length of a Curve Represented Parametrically
- The Arc Length of a Plane Curve in Rectangular Coordinates
- The Area of a Curvilinear Sector in Polar Coordinates