Complete Solutions to Area of Surface of Revolution of chapter APPLICATIONS OF THE DEFINITE INTEGRAL of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | APPLICATIONS OF THE DEFINITE INTEGRAL |
| IA MARON | Area of Surface of Revolution |
| Number Of Questions | 10 |
| Academic Year | 2023-24 |
Find the area of the surface formed by revolving the astroid `x^(2//3) + y^(2//3) = a^(2//3)` about the x-axis
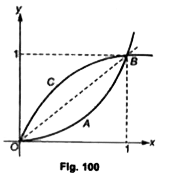
View SolutionFind the area of the surface generated by revolving about the x-axis a closed contour OABCO formed by the curves `y= x^(2) and x= y^(2)`
View SolutionThe area of the ellipse `(x^(2))/(a^(2))+(y^(2))/(b^(2))=1` is
View SolutionAn are of the catenary `y= (a)/(2) (e^((x)/(a)) + e^(-(x)/(a)))=a cos h(x)/(a)`,
whose end-points have abscissas 0 and x, respectively, revolves about the x-axis. Show that the surface area P and the volume V of the solid thus generated are related by the formula `P=(2V)/(a)`
View SolutionFind the area of the surface obtained by revolving a loop of the curve `9ax^(2)= y (3a-y)^(2)` about the y-axis
View SolutionCompute the area of the a surface generated by revolving about the x-axis an are of the curve `x= t^(2) , y= (t)/(3) (t^(2)-3)` between the points of intersection of the curve and the x-axis
View SolutionCompute the surface area of the torus generated by revolving the circle `x^(2) + [y -b]^(2)= r^(2) (0 lt r lt b)` about the x-axis
View SolutionCompute the area of the surface formed by revolving the lemniscate `rho = a sqrt(cos 2 varphi)` about the polar axis.
View SolutionCompute the area of the surface formed by revolving about the straight line `x+ y=a` the quarter of the circle `x^(2) + y^(2)=a^(2)` between A(a, 0) and B(0, a).
View SolutionComputes the area of the surface formed by revolving one branch of the lemniscate `rho=a sqrt(cos 2 varphi)` about the straight line `varphi = (pi)/(4)`
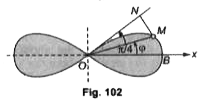
View Solution
Area of Surface of Revolution questions and complete solutions for chapter APPLICATIONS OF THE DEFINITE INTEGRAL of IA MARON MATHS (HINGLISH) of Class 12
All Exercises from IA MARON Class 12 MATHS APPLICATIONS OF THE DEFINITE INTEGRAL
- Area of Surface of Revolution
- Computing Areas in Rectangular Coordinates
- Computing Areas with Parametrically Represented Boundaries
- Computing Pressure, Work and Other Physical Quantities by the Definite Integrals
- Computing Static Moments and Moments of Inertia. Determining Coordinates of the Centre of Gravity
- Computing the Limits of Sums with the Aid
- Computing the Limits of Sums with the Aid Of Definite Integerals
- Computing the Volume of Solid
- Finding Average Values of a Function
- Geometrical Applications of the Definite Integral
- The Arc Length of a Curve in Polar Coordinates
- The Arc Length of a Curve Represented Parametrically
- The Arc Length of a Plane Curve in Rectangular Coordinates
- The Area of a Curvilinear Sector in Polar Coordinates