Complete Solutions to Electric Oscillations of chapter OSCILLATIONS AND WAVES of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | OSCILLATIONS AND WAVES |
| IE IRODOV | Electric Oscillations |
| Number Of Questions | 56 |
| Academic Year | 2023-24 |
If the elctron `(` charge of each electron `=-e)` are shifted by a small distance `x,a` net `+ ve` charge density `(` per unit area `)` is induced on the surface. This will result in an electric field `E=n ex //epsilon_(0)` in the direction of `x` and a restoring force on an electron of
`-(n e^(2)x)/(epsilon_(0))`,
Thus `m ddot(x) =-(n e^(2)x)/(epsilon_(0))`
or `ddot(x) + ( n e^(2))/( m epsilon_(0))x=0`
This gives `omega_(p)= sqrt((n e^(2))/( m epsilon_(0)))=1.645xx10^(16)s^(-1)`
as the plasma frequency for the problem,.03:13View SolutionAn oscillating circuit consisting of a capacitor with capacitance `C` and a coil of inductance `L` maintans free undamped oscillations with voltage amplitude across the capacitor equal to `V_(m)`. For an arbitrary moment of time find the relation between the current `I` in the circuit and the voltage `V` acroos the capacitor. Solve this problem usdini `Omega`'s law and then the energy conservation law.
06:21View SolutionAn oscillating circuit consists of a capacitor with capacitance `C`, a coil of inductance `L` with negligible resistance, and aswitch. With the switch disconnected , the capacitor was charged to a voltage `V_(m)` and then at the moment `t=0` the switch was closed . Find `:`
`(a)` the current `(I(t))` in the circuit as a function of time,
`(b)` the emf of self- inductance in the coil at the moments when the electric energy of the capacitor is equal to that of the current in the coil.04:47View SolutionIn an oscillating circuit consisting of a parallel- plate capacitor and an inductance coil with negligible active resistance the oscillations with energy `W` are sustained. The capacitor plates were slowly drawn aparto to increase the oscillation frequency `eta-` fold. What work was doen in the process ?
05:02View SolutionIn an oscillating circuit shown in figure, the coil inductance is equal to `L=2.5 mu F`. The capacitor have capacitances `C_(1)=2.0 mu F` and `C_(2)=3.0 mu F`. The capacitors were charged to a voltage `V=180 V`, and then the switch `S w `was closed. Find `:`
`(a)` the natural oscillation frequency,
`(b)` the peak value of the current flowing through the coil.
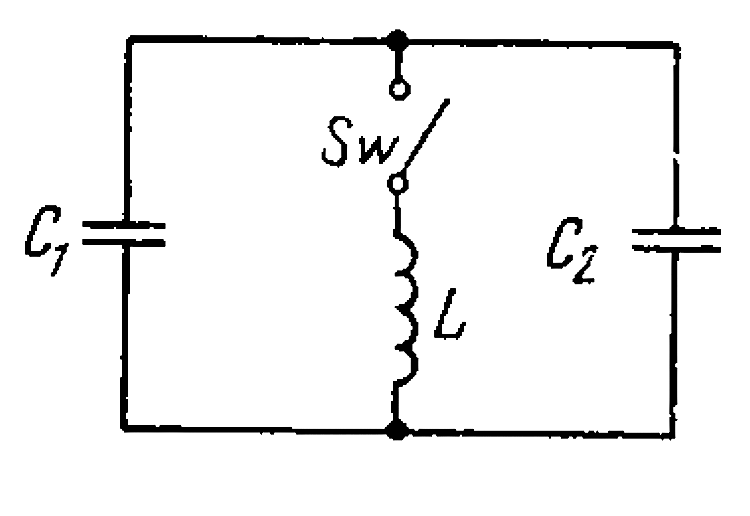 View Solution
View SolutionAn electric circuit shown in figure has a negligibly small active resistance. The left`-` hand capacitor was charged to a voltage `V_(0)` and then at the moment `t=0` the switch `Sw` was closed. Find the time dependence of the voltages in left and right capacitors.
 07:13View Solution
07:13View SolutionAn oscillating circuit consists of an inductance coil `L` and a capacitor with capacitance `C`. The resistance of the coil and the lead wires is negligible . The coil is placed in a permanent magnetic filed so that the total flux passing through all the turns of the coild is equal to `Phi` . At the moment `t=0` the magnetic field was switched off. Assuiming the switching off time to be negligible compared to the natural oscillation paeriod of the cirucuit, find the circuit current as a fuction of time `t`
04:31View SolutionThe free damped oscillations are maintained in a circuit, such that the voltage across the capacitor varies as `V=V_(m)theta^(betat) cos omegat `, Find the moments of time when the modulus of the voltage across the capacitor reaches
`(a)` peak values,
(b) maximum ( extremum ) values.01:56View SolutionA certain oscillating circuit consits of a capacitor with capacitance `C`, a coil with inductance `L` and active resistance `R`, and a switch . When the swith was disconnected, the capacitor was charged, then the switch was closed and oscillations set in. Find the ratio of the voltage across the capacitor to its peak value at the moment immediatel after closing the switch.
04:31View SolutionA circuit with capacitance `C` and inductance `L` generates free damped oscillations with current varying with time as `I=I_(m)e^(-betat) sin omegat`. Find the voltage across the capacitor as a function of time, and in particular, at the moment `t=0`.
09:31View SolutionAn oscillating circuit consist of a capacitor with capacitance `C=4.0 mu F` and a coil with inductance `L=2.0 mu H` and active resistance `R=10 Omega`. Find the ration of the energy of the coil's magnetic field to that of the capacitor's electric field at the moment when the current has the maximum value .
06:29View SolutionAn oscillating circuit consists of two coils connected in series whose inductances are `L_(1)` and `L_(2)` active resistances are `R_(1)` and `R_(2)` , and mutual inductance is negligible. These coils are to be replaced by one, keeping the frequency and the quality factor of the circuit constant. Find the inductance and the active resistance of such a coil.
00:48View SolutionHow soon does the current amplitude in an oscillating circuit with quality factor `Q=5000` decrease `eta = 2.0` times if the oscillation frequency is `v=2.2 MHz`?
01:51View SolutionAn oscillating cirucuit consits of capacitance `C=10 mu F`, inductance `L=25 Mh`, and active resistance `R=1.0 Omega. ` How mancy oscilaltion periods does it take for the current amplitude to decrease e`-` fold ?
01:56View SolutionHow much `(` in per cen `)` does the free oscllation frequency `omega` of a circuit with quality factor `Q=5.0` differ from the natural oscillation frequency `omega_(0)` of that circuit ?
02:10View SolutionIn a circuit shown in figure the battery emf is equal to `E=2.0 V`, its internal resistance is `r=9.0 Omega`, the capacitance of the capacitor is `C=10 mu F`, the coil inductance is `L=100 m H`, and the resistance is `R=100 Omega` . At a certain momenta the switch `Sw` was disconneted.
Find the energy of oscillations in the circuit
(b) `t=0.30s` after the switch was disconnected,
 03:57View Solution
03:57View SolutionDamped oscillations are induced in a cirucuit whose quality factor is `Q=50` and natural oscillation frequency is `v_(0)=5.5 kHz`. How soon will the energy stored in the circuit decrease `eta= 2.0 ` times ?
03:13View SolutionAn oscillating circuuit incorporates a leaking capacitor. Its capacitance is equal `C` and active resistance to `R`. The coil inductance is is `L`. The resistance of the coil and the wires is negligible. Find `:`
`(a)` the damped oscillation frequecy of such a circuit ,
`(b)` its quality factor.04:23View SolutionFind the quality factor of a circuit with capacitance `C=2.0 mu F` and inductance `L=5.0 mH` if the maintenance of undamped oscillations in the circuit with the voltage amplitude across the capacitor being equal to `V_(m)=1.0 V` requires a power `( :P: )=0.10m W`. The damping of oscillations is sufficiently low
View SolutionWhat mean power should be fed to an oscillating circuit with acting resistance `R=0.45 Omega` to maintain undamped harmonic oscillations with current amplitude `I_(m)=30 m A`?
01:31View SolutionAn oscillating circuit consists of a capacitor with capacitance `C=1.2 nF` and a coil with inductance `L=6.0 mu H` and active resistance `R=0.50 Omega`. What mean power should be fed to the circuit to maintain undamped harmonic oscillations with volage amplitude acroos the capacitor being equal to `V_(m) =10 V`?
03:04View SolutionFind the damped oscillation frequency of the circuit shown in figure. The capacitance `C`, inductance `L`, and active resistance `R` are supposed to be known. Find how must `C,L, `and` R` be interrelated to make oscillations possible.
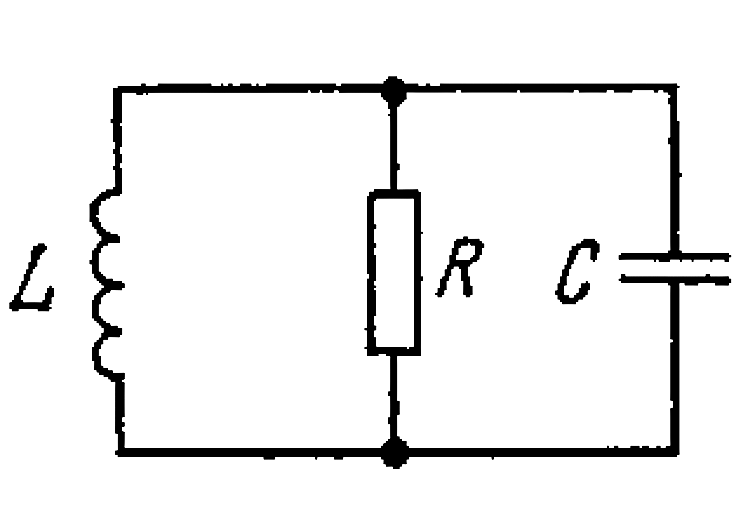 View Solution
View SolutionThere are two oscillating circuits `(figure)` with capacitors of equal capacitances. How must inductances and active resistances of the coils be interrelated for the frequencies and damping of free oscillations in both circuits to be equal ? The mutual inductance of coils in the left circuit is negligible.
 View Solution
View SolutionA circuit consists of a capacitor with capacitance `C` and a coil of inductance `L` connected in series, as well as a switch and a resistance equal to the critical value for this circuit. With the switch disconnected, the capacitor was charged to a voltage `V_(0)`, and at the moment `t=0`, the switch was closed . Find the corrent `I` in the circuit as a function of time `t`.What is `I_(max)` equal to ?
View SolutionA coil with active resistance `R` and inductance `L` was connected at the moment `t=0` to a source of voltage `V=V_(m)cos omegat.` Find the current in the coil as a function of time `t`.
06:24View SolutionA circuit consisting of a capacitor with capacitance `C` and a resistance `R` connected in series was connected at the moment `t=0` to a source of ac voltage `V=V_(m) cos omegat` . Find the current in the circuit as a function of time `t`.
06:46View SolutionA long one`-` layer solenoid tightly would of wire with resistivity `rho` has `n` turns per unit length. The thickness of the wire insulation is negligible. The cross`-` sectional radius of the solenoid is equal to `a`. Find the phase difference between current and alternating voltage fed to the solenoid with frequency `v`.
View SolutionA circuit consisting of a capacitor and an active resistance `R=110 Omega` connected in series is fed an alternating voltage with amplitude `V_(m)=110V`. In this case the amplitude of steady `-` state current is equal to `I_(m)=0.50 A`. Find the phase difference between the current and the voltage fed.
02:53View SolutionFigure illustrates the simplest ripple filter. A voltage `V=V_(0)(1+ cos omega t)` is fed to the left input. Find `:`
`(a)` the output voltabe `V^(')(t)`,
`(b)`the magnitude of the product is `eta =7.0` times less than the direct voltage component, if `omega=314 s^(-1)`.
 View Solution
View SolutionDraw the approximate voltage vector diagrams in the electric circuits shown in figure. `a,b`. The external voltage `V` is assumed to be alternating harmonically with frequency `omega`
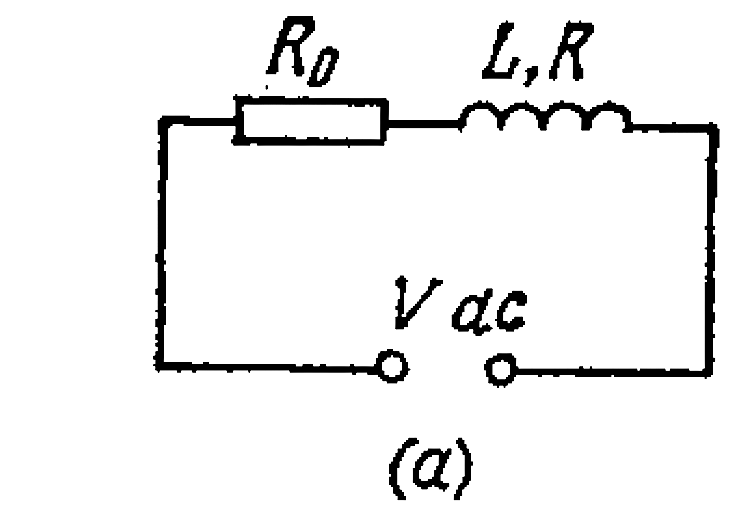
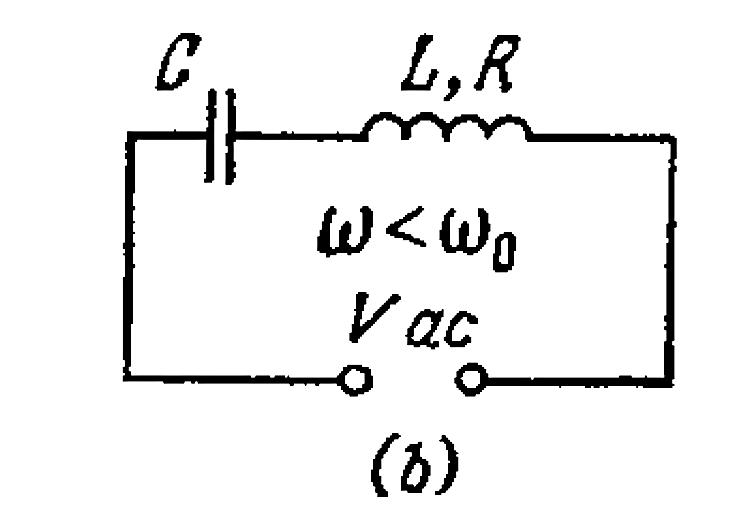 View Solution
View SolutionA series circuit consisting of a capacitor with capacitance `C=22 mu F` and a coil with active resistance `R=20 Omega` and iniductance `L=0.35 H ` is connected to a source of alternating voltage with amplitude `V_(m)=180 V` and frequency `omega=314 s^(-1)`. Find `:`
`(a)` the current amplitude in the circuit,
`(b)` the phase difference between the current and the external voltage ,
`(c)` the amplitudes of voltage across the capacitor and the coil.02:20View SolutionA series circuit consisting of a capacitor with capacitance with capacitance `C`, a rasistance `R`, and a coil with inductance `L` and negligible active resistance is connected to an oscillator whose frequency can be varied without changing the voltag amplitude. Find the frequency at which the voltage amplitude is maximum
`(a)` across the capacitor ,
`(b)` across the coil.View SolutionAn alternating voltage with frequency `omega=314s^(-1)` and amplitude `V_(m)=180 V` is fed to a series circuit consisting of a capacitor and a coil with active resistor's capacitance will the voltage amplitude across the coil be maximum ? What is this amplitude equal to ? What is the corresponding voltage amplitude across the condenser ?
View SolutionA capacitor with capacitance `C` whose interelectrode space is filled up with poorly conducting medium with active resistance `R` is connected to a source of alternating voltage `V=V_(m) cos omegat`. Find the time dependence of the steady `-` state current flowing in lead wires. The resistance of the wires is to be neglected.
View SolutionAn oscillating circuit consists of a capacitor of capacitance `C` and a solenoid with inductance `L_(1)`. The solenoid is inductively connected with a short`-` circuited coil having an inductance `L_(2)` and a negligible active resistance. Their mutual inductance coefficient is eqaul to `L_(12)`. Find the natural frequency of the given oscillating ciruit.
02:46View SolutionFind the quality factor os an oscillating circuit connected in series to a source of alternating emf if at resonance the voltage across the capacitor is `n` time that of the source.
05:49View SolutionAn oscillating circuit consisting of a coil and a capacitor connected in series if fed an alternating emf, with coil inductance being chosen to provide the maximum current in the circuuit. Find the quality factor os the system, provided an `n-`fold increase of inductance results in an `n-` fold decrease of current in the circuit.
03:22View SolutionA series circuit consisting of a capacitor and a coil with active resistance is connected to a source of harmonic voltage whose frequency can be aried, keeping the voltage amplitdue are `n` times less than the resonance amplitude. Find `:`
`(a)` the resonance frequency,
`(b)` the quality factor of the circuit.View SolutionDemonstrate thatat low damping the quality factor `Q` of a circuit maintaining forced oscillations is approximately equal to `omega_(0)//Delta omega`, where `omega_(0)` is the natural oscillation frequency , `Delta omega` is the width of the resonance curve `I(omega)` at the " height " which is `sqrt(2)` times less than the resonance current amplitude.
05:56View SolutionA circuit consisting of a capacitor and a coil connected in seried if fed two alternating voltages of equal amplitudes but different frequencies. The frequency of one voltage is equal to the natural oscillation frequency `( omega_(0))` of the circuit, the frequency of the other voltage is `eta` times highter. Find the ratio of the current amplitudes `(I_(0)//I)` generated by the two voltages if the quality factor of the system is equal to `Q`. Calculate this ratio for `Q=10` and `100,` if `eta=1.10`.
View SolutionIt takes `t_(0)` hours for a direct current `I_(0)` to charge a storage battery. How long will it take to charge such a battery from the mains using a half`-` wave rectifier, if the effective current value is also equal to `I_(0)` ?
03:26View SolutionFind the effective value of current if its mean value is `I_(0)` and its time dependence is
`(a)` shown in figure,
` (b)` `I~| sin omegat|.`
 07:44View Solution
07:44View SolutionA solenoid with inductance `L=7 m H` and active resistance `R=44 Omega` is first connected to a source of direct voltabe `V_(0)` and then to a source of sinusoidal voltage with effective value `V=V_(0)` . At what frequency of the oscillator will be power consumed by the solenoid be `eta=5.0 ` times less than in the former case ?
01:57View SolutionA coil with inductive resistance `X_(L)=30 Omega` and impedance `Z=50 Omega` is connected to the mains with effective oltage value `V=100V`. Find the phase difference between the current and the voltage, as well as the heat power generated in the coil.
View SolutionA coil with inductance `L=0.70 H` and active resistance `r=20 Omega` is connected in series with an inductance `-` free resistance `R`. An alternating voltage with effective value `V=220 V` and frequency `omega=314 s^(-1)` is a applied across the terminals of this circuit. At what value of the resistance `R` will the maximum heat power be generated in the circuit ? What is it equal to ?
02:15View SolutionA circuit consisting of a capacitor and a coil in series is connected to the mains. Varying the capacitance of the capacitor, the heat power genergated in the coil was increased `n=1.7` times. How much `(` in per cent `)` was the value of ` cos varphi` changed in the process ?
05:05View SolutionA source of sinusoidal emf with constant voltage is connected in series with an oscillating circuit with quality factor `Q=100`. At a certain frequency of the external voltage the heat power generated in the circuit reached the maximum value. How much `(` in per cent`)` should this frequency be shifted to decrease the power generated `n=2.0` times ?
05:17View SolutionA series circuit consisting of an inductance `-` free resistance `R=0.16 k Omega` and coil with active resistance is connected to the mains with effective voltabe `V=220 V`. Find the heat power generated in the coil if the effective voltage values across the resistance `R` and the coil are equal to `V_(1)=80V` and `V_(2)=180V` respectively.
08:28View SolutionA coil and an inductance `-` free resistance `R=25 Omega` are connected in parallel to the `ac1` mains. Find the heat power generated in the coil provided a current `I=0.90 A` is drawn from the mains. The coil and the resistance `R` carry currents `I_(1)=0.50 A` and `I_(2)=0.60 A` respectively.
06:44View SolutionAn alternating current of frequency `omega=314s^(-1)` is fed to a circuit consisting of a capacitor of capacitance `C=73 muF` and an active resistance `R=100 Omega` connected in parallel. Find the impedance of the circuit.
02:30View SolutionDraw the approcimate vector diagrams of currents in the circuits shown in figure. The voltage applied across the points `A` and `B` is assmed to be sinosoidal`,` the parameters of each circuit are so chosen that the total current `I_(0)` lags in phase behind the external voltage by an angle `varphi`.
 07:17View Solution
07:17View SolutionA capacitor with capacitance `C=1.0 muF` and a coil with active resitance `R=0.10 Omega` and inductance `L=1.0 m H` are connected in parallel to a source of sinusoidal voltage `V=31 V`. Find `:`
`(a)` the frequency `omega` at which the resonance sets in ,
`(b)` the effective value of the fed current in resonance , as well as the corresponding currents flowing through the coil and through the capacitor.07:42View SolutionA capacitor with capacitance `C` and a coil with active resistance `R` and inductance `L` are connected in parallel to a source of sinusoidal voltage of frequency `omega`. Find the phase difference between the current fed to the circuit and the source voltage.
View SolutionA circuit consists of a capacitor with capacitance `C` and a coil with active resistance `R` and inductance `L` connected in parallel. Find the impedane of the circuit at frequency `omega` of alternating voltage.
03:26View SolutionA ring of thin wire with active resistance `R` and inductance `L` rotates with constant angular velocity `omega` in the external uniform magneitce field perpendicular to the rotation axis. In the process , the flux of magnetic induction of external field across the ring varies with time as `Phi=Phi_(0)cos omega t`. Demonstrate that
(a) the inductive current in the ring varies with time as `I=I_(m) sin ( omegat-varphi)`, where `I_(m)=._(m) Phi//sqrt(R^(2)+ omega^(2)L^(2))` with `tan varphi=omegaL//R`,
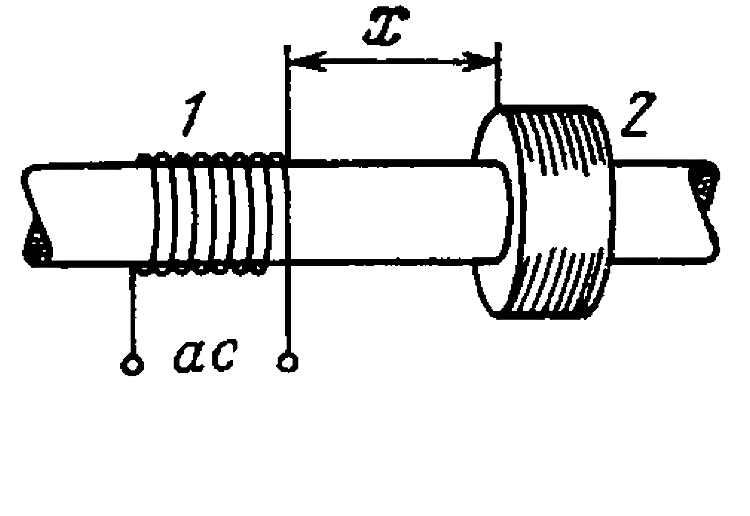
(b) the mean mechanical is defined by the formula `P=1//2 omega^(2) Phi_(0)^(2)R//(R^(2)+omega^(2)L^(2))`.04:39View SolutionA wooden core `( ` figure `)` supports two coils `:` coil `1` with inductance `L_(1)` and shor `-` circuited coil 2 with active resistance `R` and inductance `L_(2)`. The mutual inductance of the coils depends on the distance `x` between them according to the law `L_(12)(x)`. Find the mean `(` averaged over time `)` value of the interaction force between the coils when coil 1 carries an alternating current `I_(1)=I_(0)cos omegat`
 View Solution
View Solution
Electric Oscillations questions and complete solutions for chapter OSCILLATIONS AND WAVES of IE IRODOV PHYSICS (HINGLISH) of Class 12
