Complete Solutions to साधित उदाहरण of chapter रैखिक प्रोग्रामन of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | रैखिक प्रोग्रामन |
| KC SINHA HINDI | साधित उदाहरण |
| Number Of Questions | 38 |
| Academic Year | 2023-24 |
निम्नलिखित असमिका को आलेखीय विधि से हल करें।
`3y-5xlt30`
View Solution`XY` तल में असमिका `x-2yge0` को आलेखीय विधि से हल करें
View Solutionनिम्नलिखित असमिका निकाय को आलेखीय विधि से हल करें:
`x-yle2,x+yle4,xge0,yge0`
View Solutionनिम्नलिखित रैखिक असमिकाओं के निकाय को आलेखीय विधि से हल करें।
`3x+2yle24,x+2yle16,x+yle10,xge0,yge0`
View Solutionएक कम्पनी A और B नाम की दो वस्तुओं का निर्माण करती है। उसके गोदाम में केवल 100 ही नग एक समय में रखे जा सकते है ओर कारोबार में लगाने के लिए उसके पास केवल 30,000 रू0 की पूंजी है। यदि A की लागत प्रति नग 400 रू0 और B की लागत प्रति नग 900 रू0 आती हो और A को 100 रू0 और B को 120 रू0 के लाभ से बेच सकता है तो अधिकतम लाभ प्राप्त करने के लिए उसे अपनी पूंजी किस प्रकार लगानी चाहिए। यह मान लिया गया है कि वह जितने नग बनाता है उन्हें बेच लेता है। इस रैखिक प्रोग्रामन की समरूपता को गणितीय सूत्रण के रूप में लिखिए।
View Solutionरैखिक प्रोग्रामिंग इष्टतम मान (अधिकतम या न्यूनतम) को खोजने की एक विधि है जब संबंध रैखिक समीकरणों या असमानताओं के रूप में व्यक्त किया जाता है।
उपरोक्त जानकारी के आधार पर निम्नलिखित प्रश्नों के उत्तर दीजिए।
निम्नलिखित रैखिक प्रोग्रामन समस्या को आलेखीय विधि से हल करें।
`Z=60x+15y`
निम्नलिखित व्यवरोध है
`x+yle50`
`3x+yle90`
`x,yge0`
`(i)x` अक्ष पर स्थित बिंदुओ के निर्देशांक ज्ञात कीजिए
`(ii) y`अक्ष पर स्थित बिंदुओ के निर्देशांक ज्ञात कीजिए
`(iii)` प्रतिच्छेद बिन्दु के निर्देशांक ज्ञात कीजिए
`(iv)``Z=60x+15y` का अधिकतम मान क्या होगा
`(v)``Z=60x+15y` का न्यूनतम मान क्या होगा
View Solutionरैखिक प्रोग्रामिंग इष्टतम मान (अधिकतम या न्यूनतम) को खोजने की एक विधि है जब संबंध रैखिक समीकरणों या असमानताओं के रूप में व्यक्त किया जाता है।
उपरोक्त जानकारी के आधार पर निम्नलिखित प्रश्नों के उत्तर दीजिए।
निम्नलिखित रैखिक प्रोग्रामन समस्या को आलेखीय विधि से हल करें।
`z=8x+7y`
निम्नलिखित व्यवरोध है
`3x+yle66`
`x+yle45`
`xle20`
`yle40`
`x,yge0`
`(i)` `z=8x+7y` का अधिकतम मान क्या होगा
`(ii)` `z=8x+7y` का न्यूनतम मान क्या होगा
View Solutionनिम्नलखित रैखिक प्रोगामन समस्या का आलेख विधि से हल करें।
न्यूनतमीकरण करें। `z=x-5y+20`
जबकि
`x=yge0`
`-x+2yge2`
`xge3`
`yle4`
`x,yge0`
View Solutionनिम्नलिखित रैखिक प्रोग्रामन समस्या का आलेखीय विधि से हल करें। न्यूनतमीकरण करें
`z=x-7y+190`
जबकि `x+yle8`
`xle5`
`yle5`
`x+yge4`
`xge0,yge0`
View Solutionरैखिक प्रोग्रामिंग इष्टतम मान (अधिकतम या न्यूनतम) को खोजने की एक विधि है जब संबंध रैखिक समीकरणों या असमानताओं के रूप में व्यक्त किया जाता है।
उपरोक्त जानकारी के आधार पर निम्नलिखित प्रश्नों के उत्तर दीजिए।
निम्नलिखित रैखिक प्रोग्रामन समस्या को आलेखीय विधि से हल करें।
`Z=5x+3y`
निम्नलिखित व्यवरोध है
`3x+5yle15`
`5x+2yle10`
तथा `x,yge0`
`(i)x` अक्ष पर स्थित बिंदुओ के निर्देशांक ज्ञात कीजिए
`(ii) y`अक्ष पर स्थित बिंदुओ के निर्देशांक ज्ञात कीजिए
`(iii)` प्रतिच्छेद बिन्दु के निर्देशांक ज्ञात कीजिए
`(iv)Z=5x+3y` का अधिकतम मान क्या होगा
`(v)Z=5x+3y` का न्यूनतम मान क्या होगा
View Solutionनिम्नलिखित रैखिक प्रोग्रामन समस्या को आलेखीय विधि से हल करें।
न्यूनतमीकरण करें `Z=20x+10y`
जबकि
`x+2yle40`
`3x+yge30`
`4x+3yge60` तथा `x,yge0`
View Solutionनिम्नलिखित रैखिक प्रोग्रामन समस्या का हल आलेखीय विधि से करें।
न्यूनतमीकरण करें
`z=3x+5y`
जबकि
`x+yge2`
`x+3yge3`
`x,yge0`
View Solutionआलेखीय विधि से निम्नलिखित उद्देश्य फलन का न्यूनतम और महत्तम मान ज्ञात करें।
`Z=-50x+20y` जबकि
`2x-yge-5`
`3x+yge3`
`2x-3yle12`
`xge0,yge0`
View Solutionनिम्नलिखित रैखिक प्रोग्रामन समस्या का हल आलेखीय विधि से करें।
न्यूनमतीकरण तथा अधिकतमीकरण करें। `Z=3x+9y`
जबकि `x+3yle60`
`x+yge10`
`xley`
`xge0,yge0`
View Solution`5x+2y` का महत्तम तथा न्यूनतम मान ज्ञात करें जबकि
`-2x-3yle-6` अर्थात `2x+3yge6,x-2yle2,`
`6x+4yle24,-3x+2yle3`
`xge0` तथा `yge0`
View Solutionनिम्नलिखित रैखिक प्रोग्रामन समस्या को आलेखीय विधि से हल करें।
अधिकतमीकरण करें `Z=10x+6y` जबकि
`3x+yle12,2x+5yle34,x,yge0`
View Solutionनिम्नलिखित रैखिक प्रोग्रामन समस्या का हल आलेखीय विधि से करें।
अधिकतमीकरण करें `Z=50x+15y`
जबकि `: 5x+yle100,x+yle60,x,yge0`
View Solutionनिम्नलिखित रैखिक प्रोग्रामन समस्या का हल आलेखीय विधि से करें।
अधिकतमीकरण करें `z=5x+7y` जबकि
`x+yle4,3x+8yle24,10x7yle35,x,yge0`
View Solutionनिम्नलिखित रैखिक प्रोग्राम समस्या का हल आलेखीय विधि से करें।
न्यूनतमीकरण करें
`z=3x+5y` जबकि
`2x+yle4`,
`x+yge3`,
`x-2yle2`,
`x, yge0`
View Solutionनिम्नलिखित रैखिक प्रोग्रामन समस्या का हल आलेखीय विधि से करें।
न्यूनतमीकरण करें `Z=3x+5y` जबकि
`x+y=6,xle4,yle5,xge0,yge0`
View Solutionअधिकतमीकरण करें
`Z=2x+3y`
जबकि
`x+yle1`,
`x+yge3`,
`xge0,yge0`
View Solutionन्यूनतमीकरण करें `Z=3x+2y` जबकि
`x+yge8`
`3x+5yle15`
`xge0,yge0`
View Solutionएक भोज्य पदार्थ में कम से कम 80 मात्रक विटामिन A और 100 मात्रक खनिज होना चाहिए। दो प्रकार के भोज्य `F_(1)` और `F_(2)` उपलब्ध हैं। भोज्य `F_(1)` की लागत 4 रू0 प्रति मात्रक और `F_(2)` की लागत 5 रू0 प्रति मात्रक है। भोज्य `F_(1)` की एक इकाई में कम से कम 3 मात्रक विटामिन A और 4 मात्रक खनिज है। `F_(2)` की प्रति इकाई में कम से कम 6 मात्रक विटामिन A और 3 मात्रक खनिज है। हम उस आहार का न्यूनतम मूल्य ज्ञात करना चाहते हैं। जिसमें इन दो भोजयों का मिश्रण है और उसमें न्यूनतम पोषक तत्व हैं। इसको एक रैखिक प्रोग्रामन समस्या के रूप मे सूत्रबद्ध कीजिए ताकि आहार का मूल्य न्यूनतम हो।
View Solution(आहार संबंधी समस्या) एक आहार विज्ञानी दो प्रकार के भोज्यों को इस प्रकार मिलाना चाहता है कि मिश्रण में विटामिन A का घटक कम से कम 8 मात्रक और विटामिन C का घटक कम से कम 10 मात्रक हो। भोज्य I में 2 मात्रक विटामिन A प्रति kg और 1 मात्रक विटामिन C प्रति kg है। जबकि भोज्य II में 1 मात्रक विटामिन A प्रति kg और 2 मात्रक विटामिन C प्रति kg है। दिया है कि प्रति kg भोज्य I को खरीदने में 50 रू0 और प्रति kg भोज्य II को खरीदने में 70 रू0 लगते हैं। इस प्रकार के भोज्य मिश्रण का न्यूनतम मूल्य ज्ञात करने के लिए रैखिक प्रोग्रामन समस्या के रूप में सूत्रबद्ध कीजिए।
View Solution(उत्पादन संबंधी समस्या) एक निर्माणकर्ता नट और बोल्ट का निर्माण करता है। एक पैकेट नटों के निर्माण में मशीन A पर एक घंटा और मशीन B पर 3 घंटे काम करना पड़ता है जबकि एक पैकेट बोल्ट के निर्माण में 3 घंटे मशीन A पर और 1 घंटा मशीन B पर काम करना पड़ता है। वह नटों से 17.50 रू.0 प्रति पैकेट और बोल्टों पर 7.00 रू0 प्रति पैकेट लाभ कमाता है। यदि प्रतिदिन मशीनों का अधिकतम उपयोग 12 घंटे किया जाए तो अधिकतम लाभ के लिए रैखिक प्रोग्रामन समस्या का सूत्रीकरण करें।
View Solutionपरिवहन संबंधी समस्या `P` और `Q` दो स्थानों पर दो कारखाने स्थापित हैं। इन स्थानों के समान A,B,C पर स्थित तीन डिपो में भेजे जाते हैं। इन डिपो की साप्ताहिक आवश्कयता क्रमशः 5,5 और 4 समान की नग हैं जबकि `P` और `Q` पर की स्थापित कारखानों की उत्पादन क्षमता 8 और 6 नग हैं।
प्रति नग परिवहन व्यय निम्न सारणी में दिए जैसे है

परिवहन व्यय न्यूनतम होने के लिए रैखिक प्रोग्रामन समस्या का सूत्रीकरण करें।
View Solutionएक ईंट निर्माता को दो डिपो A और B है जिन पर क्रमशः 30000 एवं 20000 ईंटों का भंडार है। वह तीन मकानों `P,Q` तथा `R` से क्रमशः 15000,20000 तथा 15000 ईंट की मांग प्राप्त करता है। डिपो से मकानों तक 1000 ईंट का परिवहन खर्च निम्नलिखित है।
रैखिक प्रोगामन समस्या का सूत्रीकरण करें ताकि निर्माता को मांगों की आपूर्ति करने के लिए परिवहन खर्च न्यूनतम हो।
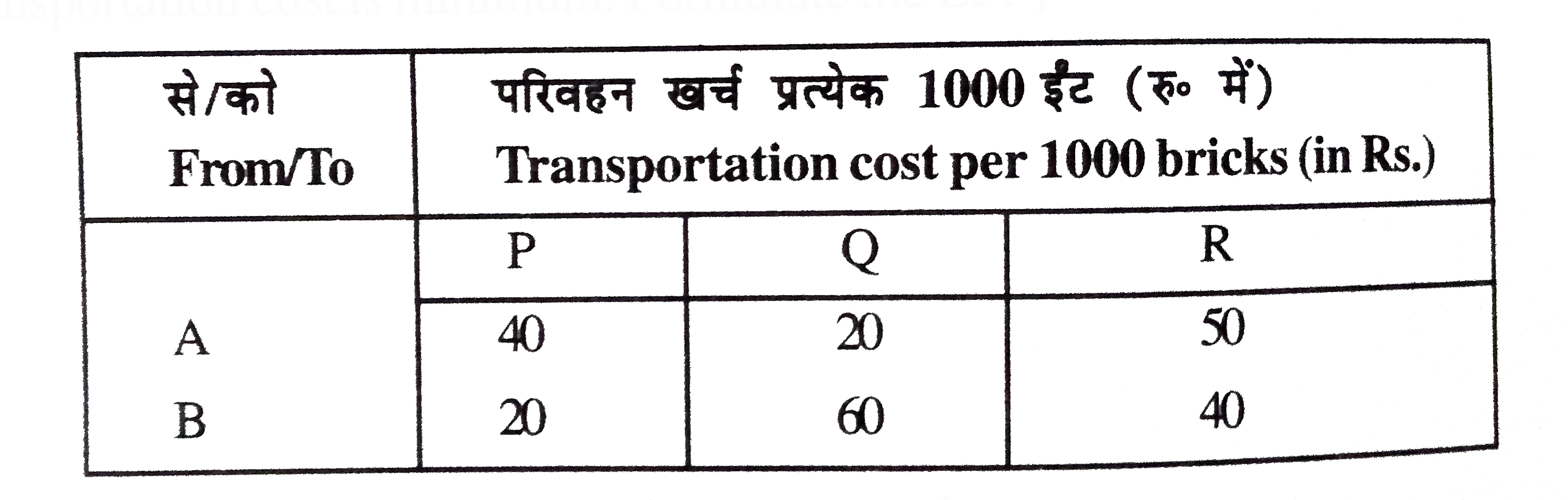
View Solution(i) एक निर्माता दो तरह के स्टील ट्रंकों का निर्माण करता है। उसके पास दो मशीन A और B हैं। प्रथम तरह के ट्रंक के निर्माण में मशीन A पर 3 घंटे और मशीन B पर 3 घंटे की आवश्कयता होती है। दूसरे तरह के ट्रंक के लिए मशीन A पर 3 घंटे और मशीन B पर 2 घंटे की आवश्यकता होती है। मशीन A और B अधिकतम प्रतिदिन क्रमशः 18 घंटे और 15 घंटे तक कार्य कर सकती है। उसे प्रथम तरह के प्रति ट्रंक 30 रू0 एवं दूसरे तरह के प्रति ट्रंक 25 रू0 का लाभ होता है। प्रत्येक तरह के कितने ट्रंक प्रतिदिन बनाए जाएं कि लाभ अधिकतम हो?
View Solutionएक निर्माता दो सामान A और B बनाता है। सामान A, 200 रू0 प्रति इकाई की दर से बिकती है और निर्माण में 30 मिनट लगते हैं। सामान B, 300 रू0 प्रति इकाई की दर से बिकती है और निर्माण में 1 घंटा लगते हैं। A की 14 इकाई और B की 16 इकाई के लिए मांग है। एक सप्ताह में 40 घंटे निर्माण कार्य होता है एवं साप्ताहिक टर्न-ओवर 10000 रू0 से कम नहीं होना है। यदि A के प्रत्येक नग पर लाभ 20 रू0 एवं B के प्रत्येक नग पर लाभ 30 रू0 हो तो प्रत्येक के कितने नगों का निर्माण किया जाए कि लाभ अधिकतम हो? अधिकतम लाभ निकालें। समस्या का हल आलेखीय विधि से निकालें।
View Solutionएक विक्रेता कुछ पंखे और सिलाई मशीन खरीदना चाहता है। उसके पास मात्र 5760 रू0 निवेश करने को है और अधिकतम 20 वस्तुओं को रखने की जगह है। एक पंखे का मूल्य 360 रू0 और एक सिलाई का मूल्य 240 रू0 है। उसे आशा है कि वह एक पंखे को 22 रू0 के लाभ पर और एक सिलाई मशीन को 18 रू0 के लाभ पर बेच सकता है। यह मानते हुए कि वह खरीदा हुआ सब सामान बच सकेगा, वह अपने धन को किस प्रकार निवेशित करे कि उसे अधिकतम लाभ मिले? आलेखीय विधिग से हल करें एवं अधिकतम लाभ निकालें।
View Solutionएक दूकानदान दो सामानों थर्मस फ्लास्क और वायुशून्य बर्तनों को बेचता है। उसे एक फ्लास्क की कीमत 120 रू0 एवं एक वायुशून्य बर्तन की कीमत 60 रू0 पड़ती है। उसके पास अधिक से अधिक 12000 रू0 निवेश के लिए है एवं 150 सामानों को रखने की जगह है। एक फ्लास्क को बेचने से 20 रू0 एवं वायुशून्य बर्तन को बेचने से 15 रू0 का लाभ होता है। यह मानते हुए कि वह जितने सामान खरीदता है बेचा सकता है उसे प्रत्येक के कितने नग खरीदने चाहिए ताकि उसका लाभ अधिकतम हो सके? आलेखीय विधि से हल करें।
View Solutionएक कारखाने का मालिक अपने कारखाने के लिए दो तरह के मशीन A और B खरीदना चाहता है। मशीन A के लिए `1000 m^(2)` का क्षेत्र एवं 12 कुशल आदमी इसे चलाने के लिए आवश्यक है एवं 50 इकाइयां इसका प्रतिदिन का अउटपुट है। मशीन B के लिए `1200m^(2)` का क्षेत्र एवं 8 कुशल आदमी की जरूरत है एवं इसका प्रतिदिन आउटपुट 40 इकाइयां हैं यदि `7600m^(2)` का क्षेत्र एवं 72 आदमी मशीन चलाने के लिए उपलब्ध हो तो प्रत्येक तरह के कितने मशीन खरीदी जानी चाहिए कि प्रतिदिन का आउटपुट अधिकतम हो।
View Solutionएक निर्माता के पास क्रमशः 30 इकाई और 17 इकाई मजदूरी और पूंजी है जिसे वह दो सामानों X और Y के निर्माण में उपयोग कर सकता है। X की 1 इकाई के निर्माण में 2 इकाई मजदूरी और 3 इकाई पूंजी की आवश्यकता होती है। Y की एक इकाई के निर्माण में 3 इकाई मजदूर और 1 इकाई पूंजी की आवश्यकता पड़ती है । यदि X और Y की कीमत प्रति इकाई क्रमशः 100 रू0 और 120 रू0 रखी जए तो वह निर्माता अपने संसाधनों का प्रयोग किस प्रकार करे कि उसका कुल रेवेन्यू अधिकतम हो सके। आलेखीय विधि से हल करें।
View Solutionडेविट बॉण्ड A और B पर अधिक से अधिक 12000रू0 निवेश करना चाहता है। नियमतः उसे बॉण्ड A में कम से कम 2000 रू0 और बॉण्ड B में 4000 रू0 निवेशित करना होगा। यदि ब्याज दर A पर 8% सालाना और B पर 10% सालाना हो तो अधिकतम ब्याज पाने के लिए उसे किस प्रकार निवेश करना चाहिए? आलेखीय विधि से हल करें।
View Solutionएक तेल कंपनी को कम से कम 13000,20000 और 15000 बैरल क्रमशः उच्च कोटि, मध्यम कोटि और निम्न कोटि के तेल की आवश्यकता है। तेल शोधक A प्रतिदिन क्रमशः 100,300 एवं 200 बैरेल उच्च कोटि, मध्यम कोटि और निम्न कोटि का तेल उत्पादित करता है जबकि तेल शोधक B प्रतिदिन क्रमशः 200,400 और 100 बैरेल उत्पादित करता है। यदि A को चलाने में 400 रू0 प्रतिदिन और B को चलाने में 300 रू0 प्रतिदिन खर्च पड़ता है तो कितने दिनों के लिए प्रत्येक को चलाना होगा ताकि आवश्यक खर्च न्यूनतम हो?
View Solutionएक बीमार व्यक्ति के लिए एक आहार से कम-से-कम विटामिन की `4000` इकाइयां , खनिज की `50` इकाइयां और कैलोरीज की `1400` इकाइयां होनी चाहिए दो भोज्य `A` और `B` उपलब्ध है जिनकी कीमत क्रमशः `4` रू और `3` रू प्रति इकाई है यदि `A` की एक इकाई में `200` विटामिन की इकाई `1` खनिज की इकाई और `40` कैलोरीज की इकाई हो एवं `B` की एक इकाई में `100` विटामिन की इकाई `2` खनिज की इकाई और `40` कैलोरीज की इकाई हो तो ज्ञात करें की भोज्यों का कैसा सम्मिश्र किया जाए की आवश्यक तत्वों को पूरा करते हुए मूल्य न्यूनतम हो ?
View Solutionएक गृहिणी दो तरह के भोज्यों X और Y इस प्रकार से मिलना चाहती हैं कि मिश्रण में कम से कम 10 इकाई विटामिन A,12 इकाई विटामिन B और 8 इकाई विटामिन C हो। X के 1 kg और Y के 1 kg में वर्तमान विटामिन निम्न सारणी में दिए गए हैं
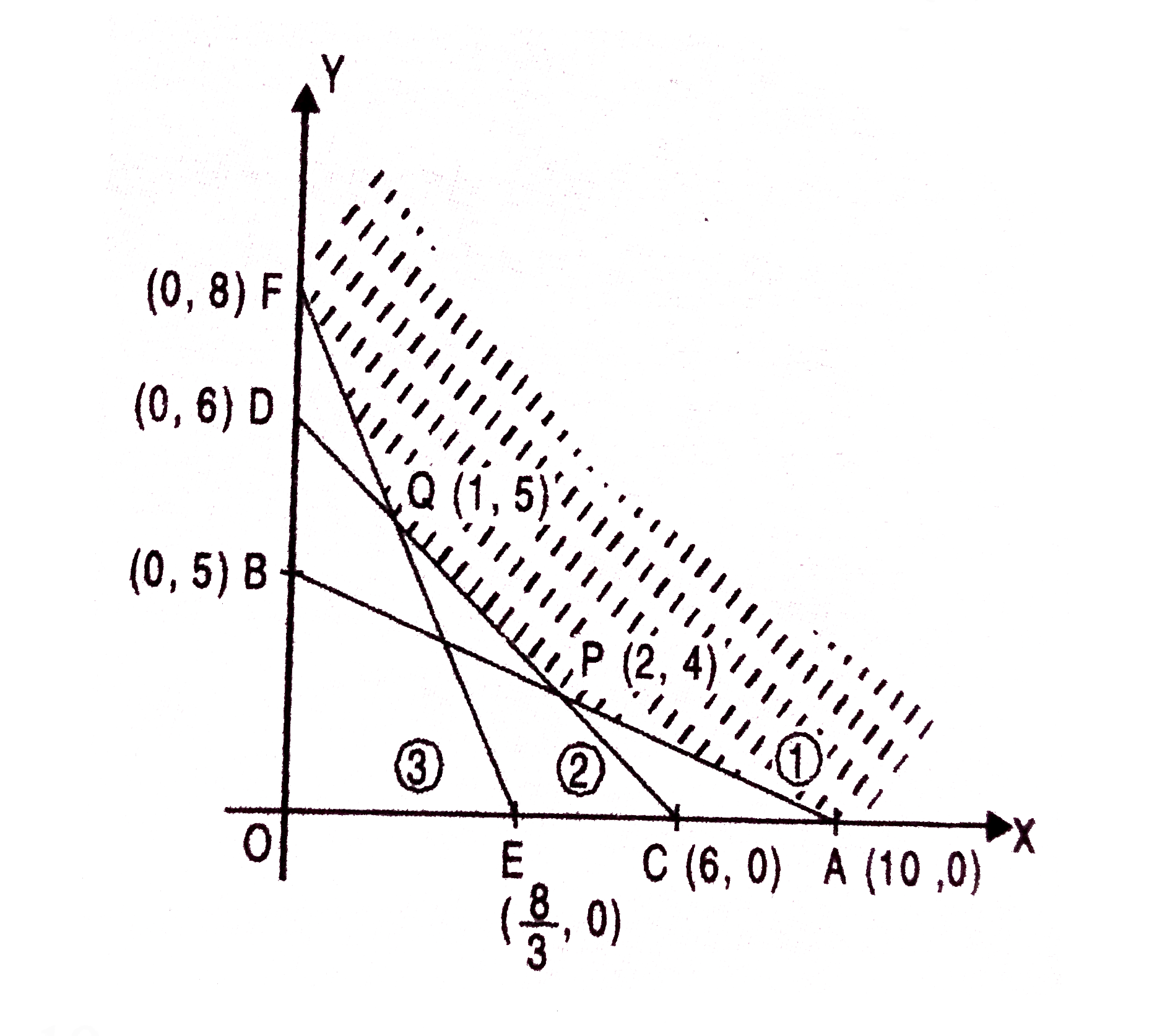
यदि X 1 का kg और Y के 1kg की कीमत क्रमशः 6 रू0 और 10 रू0 हो तो मिश्रण का न्यूनतम मूल्य ज्ञात करें जो इच्छित आहार दे सके।
View Solutionपरिवहन संबंधी समस्या : P और Q दो स्थानों पर दो कारखाने स्थापित हैं। इन स्थानों से सामान A,B,C पर स्थित तीन डिपो में भेजे जाते हैं। इन डिपो की साप्ताहिक आवश्यकता क्रमशः 7,6 और 4 समान की नग है जब कि P और Q स्थापित कारखानों की उत्पादन क्षमता 9 और 8 नग हैं
प्रति नग परिवहन व्यय निम्न सारणी बद्ध है

प्रत्येक कारखाने से कितने नग सामान प्रत्येक डिपो को भेजा जाए जिससे परिवहन व्यय न्यूनतम हो?
View Solution
साधित उदाहरण questions and complete solutions for chapter रैखिक प्रोग्रामन of KC SINHA MATHS (HINDI) of Class 12
All Exercises from KC SINHA HINDI Class 12 MATHS रैखिक प्रोग्रामन
- OBJECTIVE QUESTIONS
- SUBJECTIVE_TYPE
- एक से अधिक इष्टतम हल वाले रैखिक प्रोग्रामन समस्या के हल पर आधारित प्रश्नः
- दो चरों में एक रैखिक असमिका के हल पर आधारित प्रश्नः
- दो चरों में रैखिक असमिकाओं के निकाय के हल पर आधारित प्रश्नः
- रैखिक प्रोग्रामन समस्या के हल पर आधारित प्रश्न जब संसंगत क्षेत्र एक रेखा खण्ड है या सुसंगत क्षेत्र का अस्तित्व नहीं है:
- रैखिक प्रोग्रामन सुमस्या के हल पर आधारित प्रश्न जब संगंत क्षेत्र अपरिबद्ध है:
- साधित उदाहरण
- दिए गए रैखिक प्रोग्रामन समस्या के आलेखीय हल पर आधारित प्रश्न जब सुसंगत क्षेत्र परिमित्र या परिबद्ध है: