Complete Solutions to Paper 2 (Mathematics) of chapter PRACTICE SET 14 of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | PRACTICE SET 14 |
| MHTCET PRACTICE PAPER | Paper 2 (Mathematics) |
| Number Of Questions | 50 |
| Academic Year | 2023-24 |
The radius of the circle passing through the foci of `(x^(2))/(16) + (y^(2))/(9) =1`, and having centre (0, 3) is
View SolutionThe parabola `y^2 = 4x` and the circle `x^2 + y^2 - 6x + 1=0`
View SolutionThe equation of circle which touches the line ` y=x` at origin and passes through the point (2,1) is `x^2 + y^2 + px + qy = 0` Then ` p, q ` are
View SolutionThe measure of the chord intercepted by circle `x^2 + y^2 = 9` and the line x-y+2= 0 is
View SolutionIf `(5+9+13+..."upto n terms")/(7+9+11+..."upto 12 terms")=(5)/(12)`, then n is equal to
View SolutionThe number of solutions of the pair of equations `2s in^2theta-cos2theta=0` `2cos^2theta-3sintheta=0` in the interval `[0,2pi]` is 0 (b) 1 (c) 2 (d) 4
View SolutionIf `sin4A-cos2A=cos4A-sin2A` `("where",0ltAlt(pi)/(4))`, then the value of tan 4A is
View SolutionSolve the differential equation `(dy)/(dx)=(x(2logx+1))/((siny+ycosy))`.
View SolutionIf `sin(sin^(-1)1/5+cos^(-1)x)=1,` then find the value of `xdot`
View SolutionIn a `DeltaABC`,
`(b+c)(bc)cosA+(a+c)(ac)cosB+(a+b)(ab)cosC` is
View Solution`f(x)=(e^(2x)-1)/(e^(2x)+1)` is
View SolutionFind the length of normal to the curve `x=a(theta+sintheta),y=a(1-costheta)` at `theta=pi/2dot`
View SolutionIf `y=(x+sqrt(1+x^2))^n` then `(1+x^2)(d^2y)/(dx^2)+x(dy)/(dx)`
View Solution`(d)/(dx)[log_(e)e^(sin(x^(2)))]` is equal to
View SolutionThe area enclosed between the curve `y=log_(e)(x+e)` and the coordinate axes is
View SolutionIf `f(x)={{:((1-sinx)/(pi-2x),,","xne(pi)/(2)),(lambda,,","x=(pi)/(2)):},"be continuous at "x=(pi)/(2),` then value of `lambda` is
View SolutionThe value of `lim_(xto0) ((1-cos2x)sin5x)/(x^(2)sin3x)` is
View SolutionThe differential equation of the family of parabolas with focus at the origin and the X-axis as axis, is
View Solution`int_(-2)^(2)sin^(3)x|x|dx` is equal to
View SolutionFind the antiderivative of `f(x) = In (In x) + (In x)^-2` whose graph passes through `(e, e)`.
View SolutionA basket contains 5 apples and 7 oranges and another basket contains 4 apples and 8 oranges. One fruit is picked out from each basket. The probability that the fruits are both apples or both oranges, is
View SolutionFor the following linear programming problem minimize `Z=4x+6y` subject to the constraints `2x+3yge6,x+yle8,yge1,xge0`, the solution is
View SolutionIf `p to (~ p vvq)` is false, the truth values of p and q are , respectively
View SolutionWhich of the following pair of straight lines intersect at right angle?
View SolutionIf `bar u,bar v,bar w` are three non coplanar vectors then `(bar u+bar v-bar w).{(bar u-bar v) xx (bar v-bar w)}=`
View SolutionA five digit number is chosen at random. The probability that all the digits are distinct and digits at odd places are odd and digits at even places are even, is
View SolutionThe output s as a Boolean expression in the inputs `x_(1),x_(2)` and `x_(3)` for the logic circuit in the following figure is
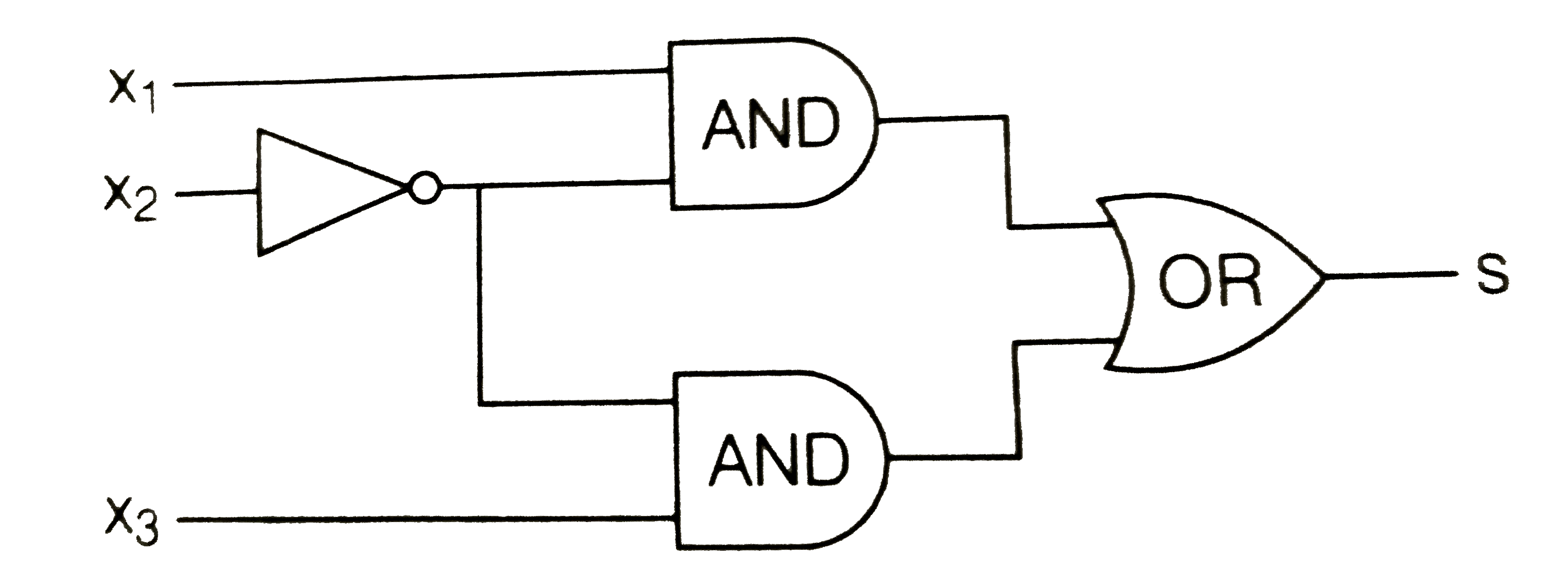
View SolutionIf `int(log"("x+sqrt(1+x^(2))")")/(sqrt(1+x^(2)))dx="gof"(x)+"constant, then"`
View SolutionIf `y=f(x)" and "ycosx+cosy=pi`, then the value of f''(0) is
View SolutionThe statement `(p rArr q) iff (~p ^^ q)` is a
View SolutionIn order that the function `f(x)=(x+1)^(cotx)` is continuous at x = 0, f(0) must be defined as
View SolutionIf `log_(x)ax,log_(x)bx" and "log_(x)cx` are in AP, where a, b, c and x, belong to `(1,oo)`, then a, b and c are in
View SolutionThe angle between the straight lines x -y `sqrt3=5 and sqrt3x +y =7 ` is
View SolutionIf S is a set with 10 elements and `A={(x,y):x,y in S, x ne y}`, then the number of elements in A is
View SolutionLet `r` be relation from `R` (set of real numbers) to R defined by `r={(a,b)|a, b in R and a-b+sqrt3` isan irrational number}. The relation `r` is
View SolutionLet `f(x)=inte^x(x-1)(x-2)dxdot` Then `f` decreases in the interval `(-oo,-2)` (b) `-2,-1)` `(1,2)` (d) `(2,+oo)`
View SolutionThe number of critical points of
`f(x)=|x|(x-1)(x-2)(x-3)` is
View SolutionThe shaded region for the inequality `x+5yle6` is
View SolutionFor an LPP, minimise Z = 2x + y subject to constraint `5x+10y le 50 , x +y ge 1,y le 4 ` and ` x,y ge 0 ` then Z is equal to
View SolutionLet [x] denotes the greatest integer less than or equal to x. If `f(x) = [x sin pix]`, then f(x) is
View SolutionIf f(0) = 0 and `f(x) =(1)/((1-e^(-1//x))) " for " x ne 0.` Then, only one of the following statements on f(x) is true. That is f(x) is
View Solution`int_(0)^(10)|x(x-1)(x-2)|dx` is equal to
View SolutionStatement I `int_(pi/6)^(pi/3)1/(1+tan^3x)` is `pi/12` Statement II `int_a^bf(x)dx=int_a^bf(a+b-x)dx`
View SolutionFunction `f(x)={x-1, x<2 and 2x-3, xgeq2` is a continuous function
View SolutionArea of the region bounded by the curves `y=2^(x),y=2x-x^(2),x=0" and "x=2` is given by :
View SolutionThe equation of plane passing through a point A(2, -1, 3) and parallel to the vectors a = (3, 0, -1) and b = (-3, 2, 2) is
View SolutionShow that the disease of the point of intersection of the line `(x-2)/3=(y+1)/4=(z-2)/12` and the plane `(x-y+z=5)` from the point `(-1,-5,-10)` is 13 units.
View SolutionIf `|A|=3,|B|=4,|C|=5" and "a,b,c` are such that each is perpendicular to the sum of other two, then `|a+b+c|` is
View SolutionIf a, b, c are three unit vectors such that `a+b+c=0`. Where 0 is null vector, then `a.b+a.c+c.a` is
View Solution`a.hati=a.(2hati+hatj)=a.(hati+hatj+3hatk)=1,` then `a` is equal to
View Solution
Paper 2 (Mathematics) questions and complete solutions for chapter PRACTICE SET 14 of MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS of Class 12