Complete Solutions to Multiple Choice Questions (LEVEL-II) of chapter HEAT AND THERMODYNAMICS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | HEAT AND THERMODYNAMICS |
| MODERN PUBLICATION | Multiple Choice Questions (LEVEL-II) |
| Number Of Questions | 55 |
| Academic Year | 2023-24 |
The P-V diagram for a cyclic process is a triangle ABC drawn in order. The co-ordinates of A, B, C are (4,1), (2,4) & (2,1). The co-ordinates are in order of P- V in which P is in `"N/m"^(2)` & volume in litres. The work done during the process from A to B is:
View SolutionIn Q.No. 69, work done in complete cycle is :
View SolutionThe density of a liquid of coefficient of cubical expansion `gamma` is d at `0^(@)C`. When the liquid is heated to a temperature T, the change in density will be :
View SolutionTwo blocks of ice join together where pressed. Which one of the following will appropriately account for this ?
View SolutionThe equation of state for a real gas such as hydrogen oxygen etc. is called the Van der waal's equation which reads: `-(P+(a)/(V^(2)))(V-b)-=n RT` where a and b are constants of the gas. The dimensional formula of constant a is:
View SolutionAn ideal gas is initiaily at temperature T and volumoeV. lts volume is increased by `Delta V` due to an increase in temperature `Delta T`, pressure remaining constant. The quantity `k = AV//(V Delta T)` varies with temperature as:
View SolutionWhich of the graphs shown in fig. correctly represents the variation of `beta =- (d_(v)// d_(p))//V` with P for an ideal gas at constant temperature:
View SolutionFor a monoatomic gas in adiabatic process, the relation between the pressure and absolute temperature time T is `P prop T` where C equal to:
View SolutionIf the degrees of freedom of a gas are f, then the ratio of its specific heats `(C_(p))/(C_(v))` is given by :
View SolutionA volume V and temperature T was obtained, as shown in diagram, when a given mass of gas was heated. During the heating process the pressure is :
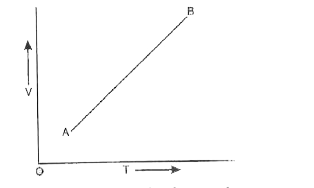
View SolutionA vessel containing air of mass 8g at 400 K is provided with a hole so that some amount of air leaks out. After some time, the pressure is halved and temperature is changed to 300 K. The mass of air escaped is:
View SolutionIf one mole of a monoatomic gas `gamma =(5)/(3)`, is mixed with one mole of diatomic gas `gamma =(7)/(5)`, what is the value of `gamma` for the mixture ?
View SolutionPure water cooled to `-15^(@)C` is contained in a thermally insulated flask. Some ice is added into the flask. The fraction of water frozen into ice is :
View SolutionOne mole of monoatomic gas is mixed with three moles of diatomic gas. What is molecular specific heat of the mixture at constant volume ? R = 8.31 J/mole/K:
View SolutionHalf a mole of helium is contained in a container at S.T.P. How much heat energy is needed to double the pressure of the gas, keeping the volume constant ? Heat capacity of the gas is 3J/g/K:
View SolutionA Carnot's engine is working between `7^(@)C and 287^(@)C`. It is desired to increase its efficiency to 70%. By how much should the temperature of source be increase ?
View SolutionWhen a gas enclosed in a closed vessel was heated so as to increase its temperature by `5^(@)C`, its pressure was seen to have increased by 1%. The initial temperature of the gas was nearly :
View SolutionOne mole of an ideal gas at an initial temperature of TK does 6 R joule of work adiabatically. If the ratio of specific heats of this gas at constant pressure and at constant volume is 5/3, the final temperature of the gas will be:
View SolutionThe temperature of equal masses of three different liquids A, B and C are `12^(@)C, 19^(@)C and 28^(@)C` respectively. The temperature when A and B are mixed is `16^(@)C` and when B and C are mixed is `23^(@)C`. The temperature when A and C are mixed is
View SolutionA Carnot engine whose sink is at 300 K has an efficiency of 40%. By how much should the temperature of source be increased so as to increase its efficiency by 50% of original efficiency:
View SolutionStatement-I: The temperature at which centigrade and Fahrenheit thermometers read the same is -`40^(@)`.
Stament-II : There is no relation between Fahrenheit and centigrade scale of temperature.
View SolutionStatement-I : It is not posible for a system, unaided by an external energy to transfer heat from a body at lower temperature to another body a higher temperature.
Statement-II: It is not possible to violate second law of thermodynamics.
View SolutionStatement-I : A beaker is completely filled with water at `4^(@)C`. It will overflow both when heated on cooled. Statement-II : There is expansion of water both below and above `4^(@)C`.
View SolutionStatement-I: Pressure and temperature are the examples of intensive variable.
Statement-II : The variable which depend upon the mass or size of the system are called intensive variable
View SolutionStatement-I : Internal energy is a state function.
Statement-II: Intemal energy of an isolated system does not change.
View SolutionRead the following paragraph and answer the following questions.
According to Kelvin Planck's statement of second law of thermodynamic no process is possible whose sole result is the adsorption of heat from a reservoir and the complete conversion of heat into work. A carnot heat engine works at temperatures `227^(@)C and 127^(@)C`. It absorbs `6.0 xx 10^(4)` calories of heat from the source at high temperature in each cycle.
The amount of heat converted into work in above carnot engine is :
View SolutionRead the following paragraph and answer the following questions.
According to Kelvin Planck's statement of second law of thermodynamic no process is possible whose sole result is the adsorption of heat from a reservoir and the complete conversion of heat into work. A carnot heat engine works at temperatures `227^(@)C and 127^(@)C`. It absorbs `6.0 xx 10^(4)` calories of heat from the source at high temperature in each cycle.
The amount of heat rejected to sink at lower temperature is:
View SolutionRead the following paragraph and answer the following questions.
According to Kelvin Planck's statement of second law of thermodynamic no process is possible whose sole result is the adsorption of heat from a reservoir and the complete conversion of heat into work. A carnot heat engine works at temperatures `227^(@)C and 127^(@)C`. It absorbs `6.0 xx 10^(4)` calories of heat from the source at high temperature in each cycle.
The efficiency of engine is:
View SolutionRead the following paragraph and answer the following questions.
According to Kelvin Planck's statement of second law of thermodynamic no process is possible whose sole result is the adsorption of heat from a reservoir and the complete conversion of heat into work. A carnot heat engine works at temperatures `227^(@)C and 127^(@)C`. It absorbs `6.0 xx 10^(4)` calories of heat from the source at high temperature in each cycle.
By how much the temperature of the sink be decreased so as to make efficiency of engine 50% keeping temp. of source fixed.
View SolutionRead the given paragraph and answer the following questions. Two moles of helium gas undergo a cyclic process as shown in fig.
Assuming the gas to be ideal
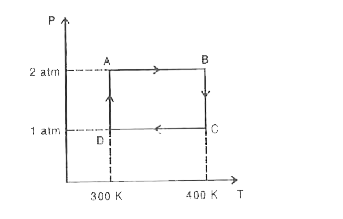
Work done from isobasic process A to B is :
View SolutionRead the given paragraph and answer the following questions. Two moles of helium gas undergo a cyclic process as shown in fig.
Assuming the gas to be ideal
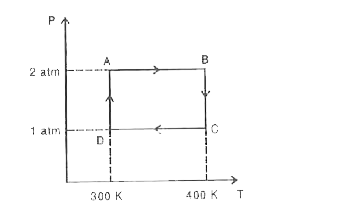
Work done during isothermal process B to C is:
View SolutionRead the given paragraph and answer the following questions. Two moles of helium gas undergo a cyclic process as shown in fig.
Assuming the gas to be ideal
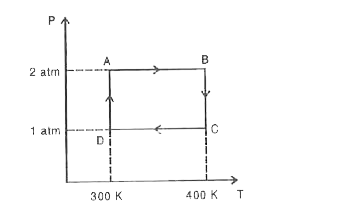
Work done during isothermal process D to A is:
View SolutionRead the given paragraph and answer the following questions. Two moles of helium gas undergo a cyclic process as shown in fig.
Assuming the gas to be ideal
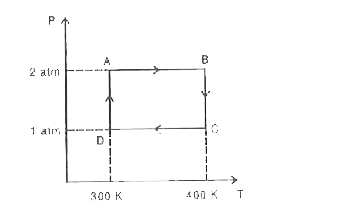
The total work done during complete cycle is :
View SolutionRead the given paragraph and answer the following questions. Two moles of helium gas undergo a cyclic process as shown in fig.
Assuming the gas to be ideal
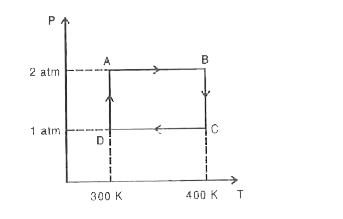
The net change in internal energy during the cyclic process is:
View SolutionRead the given paragraph and answer the following questions. Two moles of helium gas undergo a cyclic process as shown in fig.
Assuming the gas to be ideal
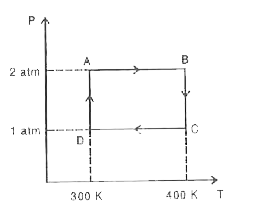
The net change in heat energy is:
View SolutionStarting with the same initial conditions, an ideal gas expands from volume `V_(1)" to "V_(2)` in three different ways. The work done by the gas is `W_(1)` if the process is purely isothermal, `W_(2)` if purely isobaric and `W_(3)` if purely adiabatic. Then SS
View SolutionA Carnot engine takes `3 xx 10^(6)` cals of heat from a reservoir at `627^(@)C` and gives it to a sink at `27^(@)C`. The work done by the engine is:
View SolutionAn ideal gas expands isothermally from a volume `V_(1)" to "V_(2)` and then compressed to original volume `V_(1)` adiabatically. Initial pressure is `P_(1)` and final pressure is `P_(3)`. Total work done is W. Then which is true :
View SolutionLiquid oxygen at 50 K is heated to 300 K at constant pressure of 1 atm. The rate of heating is constant. Which of the following graphs represents the variation of temperature with time ?
View SolutionA gaseous mixture consists of 16g of helium and 16 g of oxygen. The ratio `(C_(p))/(C_(v))` of the mixture is :
View SolutionWater of volume 2 litre in a container is heated with a coil of 1 kW at `27^(@)C`. The lid of the container is open and energy dissipates at the rate of 160 J/s. In how much time, temperature will rise from `27^(@)C" to "77^(@)C` ?
[Given specific heat of water is `4 cdot 2` kJ/kg]:
View SolutionCalorie is defined as the amount of heat required to raise temperature of 1 g of water by `1^(@)C` and it is defined under which of the following conditions ?
View SolutionA rigid container with thermally insulated walls contains a coil of resistance `100 Omega`, carrying current 1 A. Change in internal energy after 5 minute will be:
View SolutionThe work of 146 kJ is performed in order to compress one kilo mole of a gas adiabatically and in this process the temperature of the gas increases by `7^(@)C`. The gas is `(R 8 cdot 3J" mol"^(-1) K^(-1))`:
View SolutionIf `C_(p) and C_(v)` denote the specific heats of nitrogen per unit mass at constant pressure and constant volume respectively, then
View SolutionThe speed of sound in oxygen `(O_(2))` at a certain temperature `66" ms"^(-1)`, The speed of sound in helium (He) at the same temperature will be assume both gases to be ideal)
View SolutionThis question contains statement-I and statement-II of the four choice given after the statement, choose the one that best describes the two statements.
Statement I : The temperature dependence of resistance is usually given as `R = R_(0) (1 + alpha Delta t)`. The resistance of a wire changes from `100 Omega" to " 150 Omega` when its temperature is increased from `27^(@)C" to "227^(@)C`. This impilies that `alpha = 25xx 10^(-3)""^(@)C`.
Statement II: `R = R_(0) (1+ alpha Delta t))` is valid only when the change in the temperature `Delta T` is small and `Delta R= (R- R_(0)) lt lt R_(0)`.
View Solution`C_(p) and C_(v)` denote the molar specific heat capacities of a gas at constant volume and constant pressure respectively. Then
View SolutionA diatomic ideal gas is used in a Carnot engine as the working substance. If during the adiabatic expansion part of the cycle, the volume of the gas increases from V to 32 V, the efficiency of the engine is:
View SolutionA piec of ice `("heat capacity "=2100 J kg^(-1)""^(@)C^(-1) "and latent heat "=3.36 xx 10^(5) J kg^(-1))` of mass m grams is at `-5^(@)C` at atmospheric pressure. It is given 420 J of heat so that the ice starts melting. Finaly when the ice-water mixutre is in equilibrium, it is found that 1 gm of ice has melted. Assuming there is no other heat exchange in the process, the value of m is .........
View SolutionThe isothermal diagram of a gas at three different temperatures `T_(1), T_(2) and T_(3)`, is shown in the given figure. Then
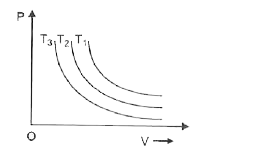
View SolutionOne mole of an ideal gas goes from an initial state A to final state B via two processes: It first undergoes isothemal expansion from volume V to 3V and then its volume is reduced from 3V to V at constant pressure. The cormect P-V diagram representing the two processes is :
View SolutionFour moles of carbon monoxide anre mixed with four moles of carbon dioxide. Asuming the gases to be ideal, the ratio of specific heats is :
View SolutionFor a monatomic ideal gas undergoing an adiabatic change, the relation between temperature and volume is `T V^(x)`= constant where x is:
View SolutionRead the two statements -(I) When a solid melts and changes to liquid state, its volume may increase on decrease. (II) As a result of increase in pressure, the melting point at a solid may be raised or lowered. With reference to these statements, the only correct statements out of the following's
View Solution
Multiple Choice Questions (LEVEL-II) questions and complete solutions for chapter HEAT AND THERMODYNAMICS of MODERN PUBLICATION PHYSICS (KANNADA ENGLISH) of Class 12