Complete Solutions to LEVEL-III of chapter ELECTROSTATICS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | ELECTROSTATICS |
| MODERN PUBLICATION | LEVEL-III |
| Number Of Questions | 23 |
| Academic Year | 2023-24 |
Two positive charges of magnitude 'q' are placed at the ends of a side (side 1 ) of a square of side 2a . Two negative charges of the same magnitude are kept at the other corners . Starting from rest , if a charge Q moves from the middle of side 1 to the centre of square , its kinetic energy at the centre of square is :
View SolutionTwo identical charged spheres suspended from a common point by two massless strings of length l are initially a distance `d (d lt lt l)` apart because to leak from both the spheres at a constant rate . As a result the charges approach each other with a velocity v . Then as a function of distance x betwee them ,
View SolutionThe electrostatic potential inside a charged spherical ball is given by `phi = ar^(2) +b` where r is the distance from the vcentre , a , b are constants . Then the charge density inside ball is :
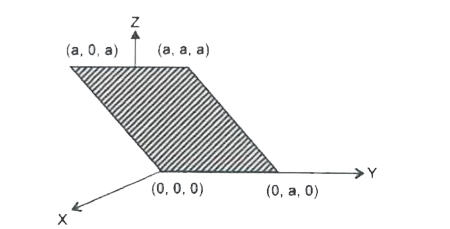
View SolutionConsider an electric field `vec(E ) = E_(0) hat(x) ` , where `E_(0)` is a constant . The flux through the shaded area (as shown in figure ) due to this field is
View SolutionA spherical metal shell A of radius `R_(A)` and solid metal sphere B of radius `R_(B) ( lt R_(A))` are kept far apart and each is given charge +Q . Now they are connected by a thin metal wire . Then
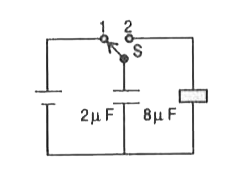
View SolutionA `2 muF` capacitor is charged as shown in the figure . The percentage of its stored energy dissiated after the switch S is turned to position 2 is :
View SolutionWhich of the field patterns below is valid for electric field as well as for magnetic field ?
View SolutionWhich of the following statements (s) is /are correct ?
View SolutionIn a uniformly charged sphere of total charge Q and radius R , the electric field E is plotted as a function of distance from the centre . The graph which would correspond to the above will be :
View SolutionAn insulating solid sphere of radius R has a uniformly positive charge density `rho` . As a result of this uniform charge distribution there is a finite value of electric potential at the centre of the sphere , at the surface of the sphere and also at a point out side the sphere . The electric potential infiniy is zero .
Statement 1 : When a charge 'q' is taken from the centre to the surface of the sphere , its potential energy changes by ` (qrho)/(3 in_(0))`
View SolutionTwo large vertical and parallel metal metal plates having a separation of 1 cm are connected to a DC voltage source of potential difference X. A poton is released at rest midway between the two plates . It is found to move at `45^(@)` to the vartical JUST after release . Then X is nearly
View SolutionConsider a thin spherical shell of radius R with its centre at the origin , carrying uniform positive surface charge density . The variation of the magnitude of the electric field ` | vec(E ) (r )|` and the electric potential V(r ) with the distance r from the centre , is best represented by which graph ?
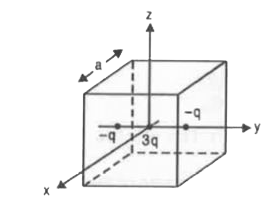
View SolutionA cubical region of side a hac its centre at the origin , it encloses three fixed point charges , -q at (0 , -a/4 , 0 ) , +3q at (0,0,0) and -q at (0,+a/4,0) . Choose the correct option (s) .
View SolutionIn the given circuit , a charge of `+80 mu C ` is given to the upper plate of the ` 4 mu F ` capacitor . Then in the steady state , the charge on the upper plate of the `3 mu F ` cpacitor is :

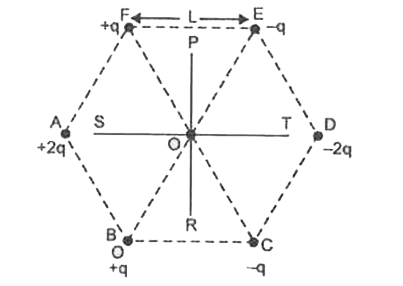
View SolutionSix point charges are kept at the vertices of a regular hexagon of the side L and centre O , as shown in the figure . Given that `K = 1/(4piepsilon_(0)) q/(L^(2))` which of the following statement (s) is (are) correct ?
View SolutionTwo charges, each equal to q , are kept at `x = - a ` and x = a on the x - axis . A particle of mass m and charge `q_(0)=q/2` is placed at the origin . If cahrge `q_(0)` is given a small disaplacement `( y lt lt a)` along the y - axis , the net force acting on the particle is proportional to :
View SolutionTwo capacitors `C_(1)and C_(2)` are charged to 120 V and 200 V respectively . It is found that by connecting them together the potential on each one can be made zero . Then :
View SolutionA charge Q is uniformly distributed over a long rod AB of lengt L as shown in the figure . The electric potential at the point O lying at a distance L from the end A is :

View SolutionA parallel plate capacitor is made of two circular plates separated by a distance of 5 mm and with a dielectric of dielectric constant 2.2 between them . When the electric field in the dielectric is `3xx10^(4)` V/m the charge density of the positive palte will be close to :
View SolutionAssume that an electric field `vec(E ) = 30 x^(2)` I exists in space . Then the potential difference `V_(A) -V_(O)` , where `V_(O) ` is the potential at the origin and `V_(A)` the potential at x = 2 m is :
View SolutionA long cylindrical shell carries positive surface charge `sigma ` in the upper half and negative surface cahrge `-sigma ` in the lower half . The electric field lines around the cylinder will look like figure given in : ( figure are schematic and not drawn to scale )
View SolutionA uniformly charged solid sphere of radius R has potential `V_(0)` (measured with respect to `oo`) on its surface . For this sphere the equiptential surfaces with potentials `(3V_(0))/2 , (5V_(0))/4, (3V_(0))/4 and (V_(0))/4` have radius `R_(1),R_(2), R_(3) and R_(4)` respectively . Then
View SolutionIn the given circuit charge `Q_(2)` on the `2muF` capacitor changes as C is varied from `1 muF "to" 3muF . Q_(2)` as a function of 'C' is given properly by : (figures are drawn schematically and are not to scale )
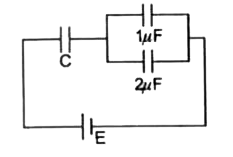
View Solution
LEVEL-III questions and complete solutions for chapter ELECTROSTATICS of MODERN PUBLICATION PHYSICS (KANNADA ENGLISH) of Class 12