Complete Solutions to LEVEL -II of chapter ELECTROSTATICS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | ELECTROSTATICS |
| MODERN PUBLICATION | LEVEL -II |
| Number Of Questions | 74 |
| Academic Year | 2023-24 |
A charge + Q is uniformly distributed over a thin ring of the radius R. The velocity of an electron at the moment when it passes through the centre O of the ring, if an electron was initially at rest at a point A which is very far always from the centre and on the axis of the ring is :
View SolutionA particle of mass m and having a charge q is placed on a smooth horizontal table and is connected to walls through unstreched springs of constant k ( shown in figure ). A horizontal electric field E parallel to spring is switched on. The maximum speed of the particle is :
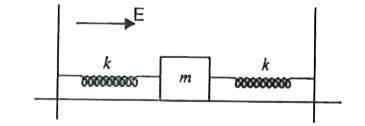
View SolutionA point particle of mass m is attached to one end of massless rigid non-conducting rod of length l. Another point particle of same mass is attached to the other end of the rod. The two particles carry equal charges +q and -q respectively. This arrangement is held in a region with the field E such that the rod makes an angle with the field direction :
View SolutionTwo balls of same radius and mass are suspended on threads of length 1 m as shown. The mass of each ball and charge is 15 g and `126 muC` respectively. When the balls are in equilibrium, the separation between them is 8 cm. The new separation between them is 8 cm. The new separation between them when one of the balls is discharged to half of origional charge. is :
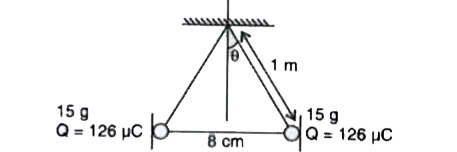
View SolutionBetween the plates of a parallel plate capacitor of capacitance C, two parallel plates, of the same material and area same as the plate of original capacitor, are placed. If the thickness of these plates is equal to` 1/5`th of distance between the plates of original capacitor, then capacitance of new capacitor is :
View SolutionA parallel plate capacitor of capacity 100 is charged by a battery of 50 V. The battery remains connected and if plates of the capacitor are brought closer so that the distance them becomes half the original distance, the additional energy given by battery to capacitor in joules is :
View SolutionFigure shows a charge arrangement known as an 'electric quadrupole' . The potential at a point on the axis of the quadrupole at a distance r from its centre is :

View SolutionTwo parallel plate capacitors of capacitance C and 2C are connected in parallel and charged to a potential difference V by a battery. The battery is then disconnected and the space between the plates of capacitor C is completely filled with a material of dielectric constant K. The potential difference across the capacitors now becomes :
View SolutionA parallel plate air capacitor is connected to a battery. The quantities charge, voltage, electric field and energy associated with this capacitor are given by`Q_(0) , V_(0), E_(0) and U_(0)` respectively. A dielectric slab is now introduced to fill the space between the plates with battery still in connection. The corresponding quantities now given by and U are related to the previous quantities as :
View SolutionA parallel plate capacitor of plate area A and plate separation d is charged to potential difference V and then the battery is disconnected. A slab of dielectric constant K is then inserted between the plates so as to fill the space between the plates. If Q, E and W denote respectively, the magnitude of charge on each plate, the electric field between the plates (after the slab is inserted), and the work done on the system in question, in the process of inserting the slab, then :
View SolutionAn infinite number of identical capacitors, each of capacitance 1 are connected as in the given figure. Then the equivalent capacitance between A and B is :
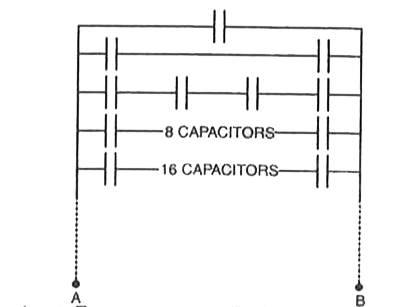
View SolutionAn electric field is uniform, and in the positive x direction for positive x, and uniform with the same magnitude but in the negative x direction for negative x. It is given that`vec( E) = 200 hat(i) N//C `for `x > 0` and`vec( E )= -200 hat(i) N//C `for `x < 0`. A right circular cylinder of length 20 cm and radius 5 cm has its center at the origin and its axis along the x-axis so that one face is at `x = +10 ` cm and the other is at`x = - 10 ` cm . What is the net outward flux through the cylinder ?

View SolutionA parallel plate capacitor has a plate area A and plate separation d . It is charged to potential V and then battery is disconnected . Now a dielectric slab of dielectric constant `epsilon_(r )` and of thickness d is inserted between plates . Find the energy change before and after insertion of the slab .
View SolutionGiven E = 5 Volt , r = 1 ohm , `R_(1)=R_(3)=1` ohm ,
`R_(2)=4 `ohm and each `C = 3 muf`
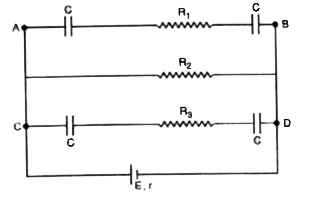
Find numerical value of the charge on each plate .
View SolutionThe numerical value of the charge on either side of the capacitor C shown in the figure is :
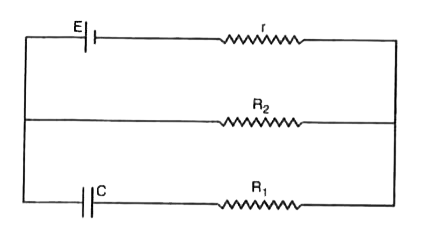
View SolutionIn the given circuit , a potential difference of 60 V is applied across AB . The potential difference between points M and N is :

View SolutionTwo identical thin rings each of radius R are coaxially placed at distance R apart . If `Q_(1) and Q_(2)` are the charges uniformly spread on the two rings , the work done is moving a charge from centre of one ring to the order is :
View SolutionA point charge of 60 stat coulomb is placed 3 cm in front of an earthed metallic plane plate of large size . Then the force of aatraction on the oint charge is :
View SolutionAn electric dipole is placed at the origin is directed along the x - axis . At a point P , far away from the dipole , the electric filed is parallel to y - axis . If OP makes an angle `theta ` with the x - axis then :
View SolutionA large flat metal surface has uniformly density `+ sigma ` An electron of mass m and charge e leaves the surfaces at point A with speed v , and return to it at oint B . The max . Value of AB is :
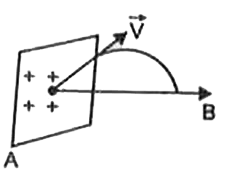
View SolutionA long string with a charge of `lambda ` per unit length passes through an imaginary cube of edge a . The max . Flux of the electric field through the cube will be :
View SolutionA solid sphere of radius R is charged uniformly . At what distance from its surface is the electrostatic potential half of the potential at the centre ?
View SolutionA solid sphere of radius R is charged uniformly . The electrostatic potential V is plotted as a function of distance r from centre of sphere . Which of the following best represents the resuling curve ?
View SolutionA non - conducting ring of radius 0.5 m carries a total charge of `1.11 xx10^(-10)` C distributed non - uniformly on its circumference , producing an electric field `vec(E )` in space . The value of line integral `int_(l = oo)^(l = 0 ) vec(E ) . vec(dl)` volt is :
View SolutionA point charge q moves from point P to S along the pasth PQRS in a uniform electric field `vec(E 0` pointing parallel to the positive direction of the axis . The co - ordinates of P,Q,R and S are (a,b,0) (2a,0,0) (a,-b,0) and (0,0,0) respectively . The work done by field in the above process is given by expression :
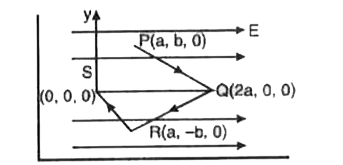
View SolutionTwo electric dipoles each of dipole moment `p = 6.2 xx10^(-3)` C cm are placed with their axis along the same line and their centres at a disatnce `d = 10^(-8)` m . What is force of attraction between dipoles ?
View SolutionTwo diploes of moments `5xx10^(-12)` cm frm a cross with their axis ( - to +) along the co- ordinate axes . Calculate potential at a point 20 cm away in a direction making an angle `30^(@)` with axis
View SolutionA copper rod AB of length l is rotated about end A with a constant angular velocity `omega` . Find electric field at a distance x from the axis of rotation .
View SolutionA thin half ring of radus 20 cm is uniformly charged with a total charge of 0.7 nC . Find the magnitude of electric field at the centre of half ring .
View SolutionA thin copper ring of radius a is charged with q units of electricity . An elctron is placed at the centre of the of electricity . An electron is placed at the centre of the copper ring . If the electron is displaced of a little , it will have frequency :
View SolutionTwo identical positive charges are placed at the diagonally opposite corners of a square . Two more identical but negative charges are placed at the other two corners. What is the work done in putting all the charges together at the centre . If q is the magnitude of each charge and 2a is the length of each of the square ?
View SolutionFind the ptential at the centre of a hemisphere of radius R charged uniformly with charge density `rho` .
View SolutionWhat is electric field at the centre of hemisphere ?
View SolutionTwo equal point charges are fixed at x = -a and ` x = +a ` on x - axis . Another point charge Q is placed at the origin . The change in electrical pot . Energy of Q , when it is displaced by small distance 'x' along x - axis is approximately to :
View Solution7 capacitors , each of capacitance `2 muF` are to be connected in a circuit to obtain total capacitance of `10/11 mu F `. A suitable combination to achieve this result is :
View SolutionA charge +q is fixed at each of the points `x = x_(0) , x = 3x_(0),x = 5x_(0)` upto infinity and a charge q is fixed at each of points `x = 2x_(0),x=4x_(0),x=6x_(0)` upto infinity . Here `x_(0)` is + ve const . The pot . At origin of this system of charges is :
View SolutionA charge Q id distributed over two concentric netal shells of radii r and `R( gt r)` such of the two shells are equal . The charge density of the inner sphere is
View SolutionTwo identical conducting balls have positive charges `q_(1)!= q_(2)` respectively . The balls are brought together so that they touch and then put back in their original positions . The force between the ball is :
View SolutionFor circuit the equivalent capacitance between points P and Q is :
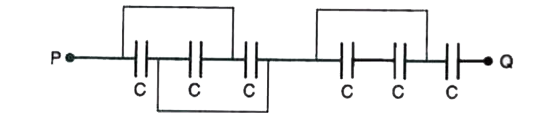
View SolutionFour identical capacitors are connected in series with a 10 V battery as shown in the figure . Potentials at A and B are
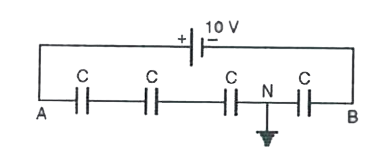
View SolutionStatement - 1 : The electric field in two dielectric slabs of different dielectric constants placed in same parallel plate capacitor may be equal .
Statement - 2 : The electric filed intensity at interface of two dielectric is always continuous .
View SolutionA point charge + q is placed at the centres of a conducting spherical shell of radius R . The shell is now given a charge + Q and a charge `+q_(0)` is placed at a distance ` r ( gt R)` from q .
View SolutionThe net force experienced by q is :
View SolutionThe charge on the outer surface of the shell is :
View SolutionThe distance between the plates of a parallel plate capacitor is 0.05 m . A field of `3xx10^(4)` V m is established between the plates . It is then disconnected from the battery and an uncharged metal plate of thickness 0.01 m is inserted into the capacitor parallel to its plates .
The potential difference between the plates before the introduction of the metal plates is :
View SolutionThe distance between the plates of a parallel plate capacitor is 0.05 m . A field of `3xx10^(4)` V m is established between the plates . It is then disconnected from the battery and an uncharged metal plate of thickness 0.01 m is inserted into the capacitor parallel to its plates .
The potential difference between the plates after the introduction of the metal plate is :
View SolutionConsider a region inside which there are various types of charges but the total charge is zero . At points outside the region
View SolutionTwo charges - q each are fixed separated by distance 2d . A third charge q of mass m placed at the mid - point is displaces slightly by `x ( x lt lt d)` perpendicular to the line joining the two fixed charges as shown in Fig. The oscillation of time period is :

View SolutionA parallel plate capacitor of area A , plate separation d and capacitance C is filled with three different dielectric materials having dielectric constant `K_(1),K_(2)and K_(3)` as shown in fig . If a single dielectric material is to be used to have the same capacitance C in this capacitor , then its dielectric constant K is given by :

View SolutionTwo equal point charges are fixed at ` x = - a and x = + a ` on the x - axis . Another point charge Q is placed at the origin . The change in the electrical potential energy of Q , when it is displaced by a small disatnce x along the x - axis , is approximately proportional to :
View SolutionTwo identical capacitors , have the same capacitance C . One of them is charged to potential `V_(1)` and the other to `V_(2)` .The negative needs of the capacitors are connected together . When the positive ends are also connected , the decrease in energy of the combined system is :
View SolutionA thin spherical conducting shell of radius R has a charge q , Another charge Q placed at the centre of the shell . The electrostatic potential at a point P at a distance `R/2` from the centre of the shell is :
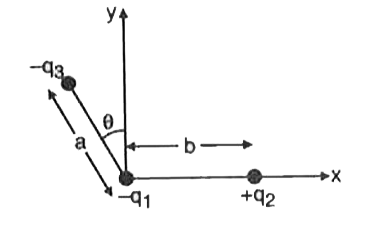
View SolutionThree charges `-q_(1)+q_(2)and -q_(3)` are placed as shown in the figure . The x - component of the force on `-q_(1)` is proportional to :
View SolutionTwo spherical conductors B and C having equal radii and carrying equal charges on them repel each other with a force F when kept apart at some distance . A third ssherical conductor having same radius as that of B but uncharged is brought in contact with B , then brought in contact with C and finally removed away from both . The new force of repulsion between B and C is :
View SolutionA charged particle q is fired towards another charged particle Q which is fixed , with a speed v . It approaches Q upto a closet distance r and then returns . If q is given speed 2 v , the closest distance of approach would be :
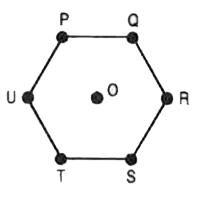
View SolutionSix charges three positive and three negative of equal magnitude are to be placed at the vertices of a regular hexagon such that the electric field at O is double the electric field when only one positive charge of same magnitude is placed at R . Which of the following arrangements of charges is possible for P,Q,R,S,T and U respectively :
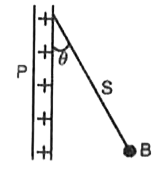
View SolutionA charged ball B hangs from a silk thread S , which makes an angle `theta ` with a large charged conducting sheet P , as shown in the figure . The surface charge density `sigma ` of the sheet is proportional to :
View SolutionTwo point charges +8q and -2q are located at x = 0 and x = L respectively . The location of a point on a x - axis at which the net electric field due to these two point charges is zero from charge 8q is :
View SolutionTwo thin wire rings having a radius R are placed at a distance d apart with their axes coinciding . The charges on the two rings are + q nd - q . The potential difference between the centres of the two rings is
View Solution3 infinite long charged sheets of charge densities ` - sigma , -2 sigma and sigma ` are placed parallel to x - y plane at z = 0 , z = a and z = 3 a . Electric field at point P is
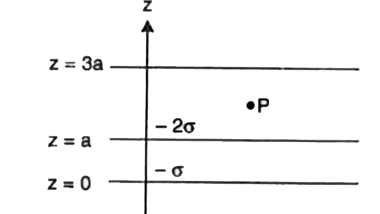
View SolutionA capacitor of 2.5 `muF` is charged through a resistor of 4 `M Omega ` . In how much time will potential drop across capacitor will become 3 times that of resistor (In 2 = 0.693)
View SolutionTwo spherical conductors A and B of radii 1 mm and 2 mm are separated by a distance of 5 cm and are uniformly charged . If the spheres are connected by a conducting charged . If the spheres are connected by a conducting wire then in equilibrium condition , the ratio of the magnitude of the eleectric fileds at the surface of spheres A and B is :
View SolutionSpherical symmetric charge system centred at origin electric potential `phi = Q/(4piin_(0)R_(0)) r le R_(0)`
`= Q/(4piin_(0)r ) , r R_(0)` :
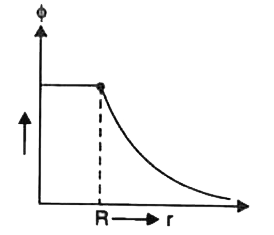
View SolutionA long , hollow conductng cylinder is ept coaxially inside another long , hollow conducting cylinder of larger radius . Both the cylinders are intially electrically neutral .
View SolutionTwo particle of mass m each are tied at the ends of a light string of length 2a . The whole system is kept on a frictionless horizontal surface with the string held tight so that each mass is at a distance 'a' from the centre P (as shown in the figure ) . Now , the mid - point

The string is pulled vertcally upwards with a small but constant force F . A s a result , the particles move towards each other on the surface . the magnitude of acceleration , when the separation between them becomes 2x , is :
View SolutionA parallel plate capacitor with air between the plates has a capacitance of 9 pF . The seperation between its plates is d . The space between the plates is now filled with two dielectriecs . One of the dielectric has dielectric constant `k_(1)=3` and thickness d/3 while the other one has dielectric constant `k_(2) = 6 ` and thickness 2d/3 Capacitance of the capactor is now .
View SolutionConsider a system of three charges q/3 ,q/3 and 2q/3 placed at points A, B and C respectively , as shown in the figure .Take O to be the centre of the circle of radius R and angle `CaB = 60^(@)`

View SolutionA parallel plate capacitor C with plates of unit area and separation d is filled with a liquid of dielectric constant K = 2 . The level of liquid is d/3 initially . Suppose the liquid level decreases at a constant speed v , the time constant as a function of time is :

View SolutionLet p (r ) = `Q/(piR^(4))` r be charge density distribution for a solid sphere of radius R and total charge Q . For a point P inside the sphere at distance `r_(1)` from centre of sphere , the magnitude of electric field is :
View SolutionThree concentric metallic spherical shells of radii R , 2R 3R are given charges `Q_(1),Q_(2),Q_(3)` respectively . It is found that the surface charge densities on the outer surfaces of the shells are equal . Then , the ratio of the charges given to the shells `Q_(1):Q_(2):Q_(3)` is :
View SolutionA thin semi - circular ring of radius r has a positive charge q distributed uniformly over it . The net field `vec(E ) ` at the centre O is :

View SolutionLet there be a spherically symmetric charge distribution with charge density varying as `rho (r ) = 0 ` for ` r gt R ` where r is the distance from the origin . The electric field at a distance ` r ( r lt R)` from the origin is given by :
View SolutionA uniformly charged thin spehrical shell of radius R carries uniform surface charge density of `sigma ` per unit area . It is made of two hemispherical shells held together by pressing them with force F . Is proportional to :

View SolutionA tiny spherical oil drop carrying a net charge q is balanced in still air with a vertical uniform electric field of strength `(81pi)/7 xx10^(5) "Vm"^(-1)` . When the field is switched off , the drop is observed to fall with terminal velocity `2xx10^(-3) "ms"^(-1) ` Given `g = 9.8 "ms"^(-2)` viscosity of the air ` = 1.8 xx10^(15) Ns m^(-2)` and the density of oil `= 900 " kg "m^(-3)` the magnitude of q is :
View Solution
LEVEL -II questions and complete solutions for chapter ELECTROSTATICS of MODERN PUBLICATION PHYSICS (KANNADA ENGLISH) of Class 12