Complete Solutions to Multiple choice questions (Level - II) Paragraph questions of chapter 15 MAGNETIC EFFECTS OF CURRENTS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | 15 MAGNETIC EFFECTS OF CURRENTS |
| MODERN PUBLICATION | Multiple choice questions (Level - II) Paragraph questions |
| Number Of Questions | 42 |
| Academic Year | 2023-24 |
A uniform and constant magnetic field ` vec(B) = (20 vec(i) - 30 vec(j) + 50 vec(k))` tesla exists in space . A charged particle with charge to mass ratio ` ((q)/(m)) = (10^(3))/( 19) C` / kg enters this region at time t = 0 with a velocity `vec (V) = (20 vec(i) + 50 vec(j) + 50 vec(j) + 30 vec(k))` m/s . Assume that the charged particle always remains in space having the given magnetic field (Use `sqrt(2) = 1.4` )
During the further motion of the particle in the magnetic field , the angle between the magnetic field `vec(B)` and velocity of the particle is
View SolutionA uniform and constant magnetic field ` vec(B) = (20 vec(i) - 30 vec(j) + 50 vec(k))` tesla exists in space . A charged particle with charge to mass ratio ` ((q)/(m)) = (10^(3))/( 19) C` / kg enters this region at time t = 0 with a velocity `vec (V) = (20 vec(i) + 50 vec(j) + 50 vec(j) + 30 vec(k))` m/s . Assume that the charged particle always remains in space having the given magnetic field (Use `sqrt(2) = 1.4` )
The frequency of the revolution of the particle in cycles per second will be :
View SolutionA uniform and constant magnetic field ` vec(B) = (20 vec(i) - 30 vec(j) + 50 vec(k))` tesla exists in space . A charged particle with charge to mass ratio ` ((q)/(m)) = (10^(3))/( 19) C` / kg enters this region at time t = 0 with a velocity `vec (V) = (20 vec(i) + 50 vec(j) + 50 vec(j) + 30 vec(k))` m/s . Assume that the charged particle always remains in space having the given magnetic field (Use `sqrt(2) = 1.4` )
The pitch of the helical path of the motion of the particle will be :
View SolutionThe ratio of magnetic field and magnetic moment at the centre of a current carrying circular loop is x . When both the current and radius is double then the ratio
View SolutionA cell is connected between the points A and C of a circular conductor ABCD of centre O with angel AOC ` = 60^(@) . If `B_(1)` and B_(2)` are the magnitudes of the magnetic field at O due to the currents in ABC and ADC respectively , the ratio `(B_(1))/(B_(2))` is

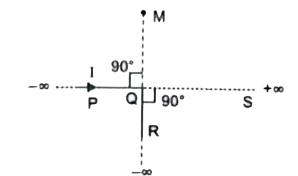
View SolutionAn infinitely long conductor PQR is bent to form a right angle as shown. A current I flows through PQR . The magnetic field due to this current at the point M is `H_(1) ` Now another infinitely long straight conductor QS is connected at Q so that the current is I/2 in QR as well as in QS, the current in PQ remaining unchanged. The magnetic field at M is now `H_(2)` The ratio `H_(1)//H_(2)` is given bY
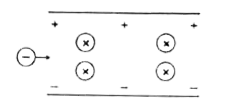
View SolutionAn electron enters the space between the plates of a charged capacitor as shown. The charge density on the plate is `sigma` . Electric intensity in the space between the plates is E . A uniform magnetic field B also exists in that space perpendicular to the direction of E . The electron moves perpendicular to both `vec(E) and vec(B)` without any change in direction . The time taken by the electron to travel a distance l in that space is
View SolutionTwo very long, straight and parallel wires carry steady current I and I respectively . The distance between the wires is d . At a certain instant of time ,a point charge q is at a point equidistant from the two wires in the plane of the wires . Its instantaneous velocity v is perpendicular to this plane . The magnitude of the force due to the magnetic field acting on the charge at this instant is
View SolutionA steady current i flows in a small square loop of wire of side L in a horizontal plane. The loop is now folded about its middle such that half of it lies in a vertical plane .let ` vec(mu)_(1) and vec(mu)_(2)` respectively denote the magnetic moments due to the current loop before and after loading . Then
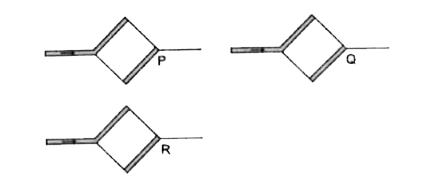
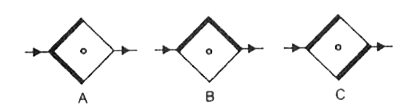
View SolutionTwo thick wires and two thin wires, all of the same materials and same length form a square in the three different ways P, Q and R as shown in fig. with current connection shown . The magnetic field at the centre of the square is zero in cases
View SolutionGraph of force per unit length between two long parallel current carying conductors and the distance between them is :
View SolutionAn electron is projected with uniform velocity along the axis of a current carrying long solenoid . Which of the following is true ?
View SolutionA circular current loop of magnetic moment M is in an arbitrary orientation in an external magnetic field B . The work done to rotate the loop by `30^(@)` about an axis perpendicular to its plane is :
View SolutionA cubical region of space is filled with some uniform electric and magnetic field . An electron enters the cube across one of its faces with velocity v and a positron eters via opposite face with velocity - v .At this instant
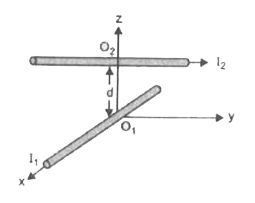
View SolutionTwo long wires carrying current `I_(1) and I_(2)` are arrangement as shown in Fig. The one carrying current `I_(1)` is along is the x-axis .The other carrying current `I_(2)` is along a long parallel to the y-axis given by x=0 and z=d . The force exerted at `O_(2)` because of the wire along the x-axis is :
View SolutionA current carrying loop consists of 3 identical quarter circles of radius R, lying in the positive quadrants of the x-y, y-z, and z-x planes with their centres at the origin joined together. The direction and magnitude of B at the origin is :
View SolutionA long straight wire carrying current of 25 A rests on a table as shown in Fig. Another wire PQ of length 1 m, mass 2.5 g carries the same current but in the opposite direction. The wire PQ is free to slide up and down. To what height will PQ rise ?
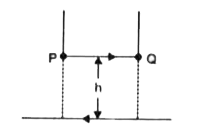
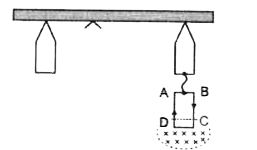
View SolutionA 100 turn rectangular coil ABCD (in XY plane) is hung from one arm of a blance (Fig.) . A mass 500 g is added to the other arm to balance the weight of the coil . A current 4.9 A passes through the coil and a constant magnetic field of 0.2 T acting inward (in xz plane)is switched on such that only arm CD of length 1 cm lies in the field . How much additional mass 'm' must be added to regain the balance ?
View SolutionA rectangular conducting loop consists of two wires on two opposite sides of length l joined together by rods of length d . The wires are each of the same material but with cross-section differing by a factor of 2.The thicker wire has a resistance R and the rods are of low resistance,which in turn are connected to a constant voltage source `V_(0)` .The loop is placed in uniform a magnetic field B at `45^(@)` to its plane. Find the torque exerted by the magnetic field on the loop about an axis through the centres of rods
View SolutionAn electron and a positron are released from (0,0,0) and (0,0,1.5R) respectively , in a uniform magnetic field `B B_(0) hat(i)` each with an equal momentum of magnitude p = e BR , Under what conditions on the direction of momentum will the orbits be non-intersecting cirecles ?
View SolutionWhat is the magnetic field at O due to current in the infinite wire forming a loop as shown in the following figure

View SolutionA cube made of wires of equal length is connected to a battery as shown in the figure.The magnetic field at at the centre of the cube is :

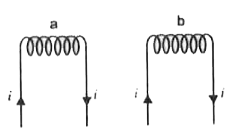
View SolutionIn the adjoining figure the coils a and b have the same number of turns and length . Each has a flux density B in the middle and a flux density B/2 at the ends when carrying the same current i . what the coils are joined to form a long coil of twice the length of a or be and the current i is sent through the coil, the flux density in the middle is given by
View SolutionTwo thick wires and two thin wires, all of the same materials and same lengths, form a squar in three different ways A,B and C as shown in the figure . With correct connections shows, the magnetic field at the centre of the square is zero in case of :
View SolutionA long wire bent as shown in the figure carries current i. if the radius of the semi-circular portion is r. the magnetic induction at the centre O is :
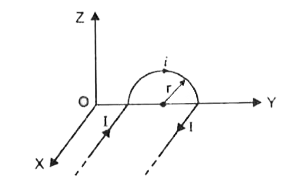
View SolutionFour wires each of length 2.0 metre are bent into four loops, P,Q,R and S and then suspended in a uniform magnetic field . Same current is passed in each loop . Which statement is correct ?
View SolutionA small current loop has a magnetic field `B_(1)` at a point on the axis and `B_(2)` at a point at the same distance in its plane. Then numerically.
View SolutionTwo long straight conductors with currents `i_(1) and i_(2)` are placed along A and B axes. The equation of locus of points of zero magnetic induction is :
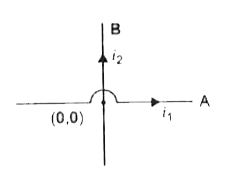
View SolutionA particle of mass m and charge q moves with a constant velocity v along the positive x directon . It enters a region containing a uniform magnetic field B directed along the negative z direction ,extending from z=a to x=b . The minimum value of v required so that the particle can just enter the region `x gt b` is
View SolutionFor a particle charged positively moving in a x-y plane initially along the x-axis , there is a sudden change in path due to the presence of x-y plane and is found to be non-circular .Which of the following combination is possible ?

View SolutionA conducting loop carrying a current I is placed in a uniform magnetic field pointing into the plane of paper as shown. The loo will have a tendency to :

View SolutionAn `e^(-)` is moving in X-Y plane along + ve x-axis . There is a sudden change in its path due to the presence of electric field and/or magnetic field beyond P as shown in fig. The curved path lie in X-Y plane and is found to be non-circular. Which of the following combinations is possible :
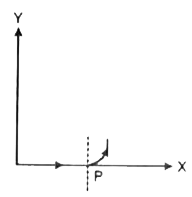
View SolutionAn electron moving with a speed u along the positive x-axis at y = 0 enters a region of uniform magnetic field ` vec(B) = - B hat(k)` which exists to the right of y-axis . The electron exists from the region after some time with the speed v at co-ordinate y then :

View SolutionA moving coil galvanometer has 150 divisions. Its current sensitivity in 10 divisions per milli ampere and voltage sensitivity is 2 divisions per milli-volt .In order that each division reads 1 volt , the resistance required to be connected in series with coil will be :
View SolutionCurrent `I_(1)` is flowing out from the plane of paper . A steady state current `I_(2)` is flowing in the loop ABCD
View SolutionA horizontal overhead powerline is at a height of 4 m from the ground and carries a current of 100 A from east to west. The magnetic field directly below it on the ground is `(mu_(0) = 4 pi xx 10^(-7) T mA^(-1))`
View SolutionA particle of mass m and charge q moving with velocity V enters region II normal to the boundary as shown in the figure. Region II has a uniform magnetic field B perpendicular to the plane of the paper .The length of the Region II is l . Choose the correct choice (s).
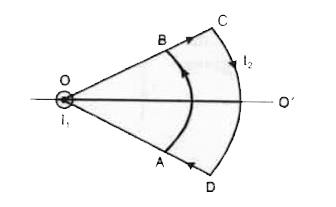
View SolutionA current loop ABCD is held fixed on the plane of the paper as shown in the figure . The arcs BC (radius = b) and DA (radius = a) of the loop are joined by two straight wires AB and CD . A steady current I is flowing in the loop . Angle made by AB and CD at the origin O is `30^(@)` Another straight thin wire with steady current `I_(1)` flowing out of the plane of the paper is kept at the origin .
The magnitude of the magnetic field (B) due to loop ABCD at the origin (O) is :
The magnitude of the magnetic field (B) due to loop ABCD at the origin (O) is :
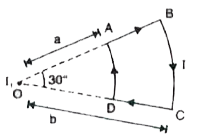
View SolutionA current loop ABCD is held fixed on the plane of the paper as shown in the figure . The arcs BC (radius = b) and DA (radius = a) of the loop are joined by two straight wires AB and CD . A steady current I is flowing in the loop . Angle made by AB and CD at the origin O is `30^(@)` Another straight thin wire with steady current `I_(1)` flowing out of the plane of the paper is kept at the origin .
Due to the presence of the current `I_(1)` at the origin
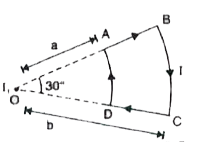
View SolutionTwo long parallel wires are at a distance 2d apart. They carry steady equal currents flowing out of the plane of the paper . As shown in Fig . The variation of the magnetic field B along the line X X' is given by :
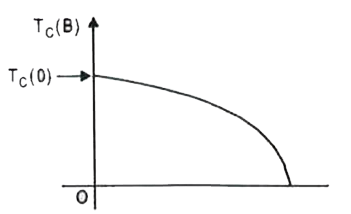
View SolutionElectrical resistance of certain materials,knows as superconductors, changes abruptly from a nonzero value to zero as their temperature is lowered below a critical temperature `T_(C) (0)`
An interesting property of superconductors is that their critical temperature becomes smaller than `T_(C) (0)` if they are placed in a magnetic field i.e., the critical temperature `T_(C)` (B) is a function of the magnetic field strength B . The dependence of `T_(C)` (B) is shown in the fig
In the graphs ahead, the resistance R of a superconductor is shown as a function of its temperature T for two different magnetic field `B_(1)` (solid line) and `B_(2)` (dashed line). If `B_(2)` is larger than `B_(1)` which of the following graphs shows the correct variation of R with T in these fields ?
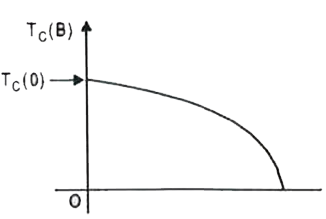
View SolutionElectrical resistance of certain materials,knows as superconductors, changes abruptly from a nonzero value to zero as their temperature is lowered below a critical temperature `T_(C) (0)`
An interesting property of superconductors is that their critical temperature becomes smaller than `T_(C) (0)` if they are placed in a magnetic field i.e., the critical temperature `T_(C)` (B) is a function of the magnetic field strength B . The dependence of `T_(C)` (B) is shown in the fig
A superconductor has `T_(C) (0) = 100` K. When a magnetic field of 7.5 Tesla is applied its `T_(C) ` decreases to 75 K for this material one can definitely say that when :
View Solution
Multiple choice questions (Level - II) Paragraph questions questions and complete solutions for chapter 15 MAGNETIC EFFECTS OF CURRENTS of MODERN PUBLICATION PHYSICS (KANNADA ENGLISH) of Class 12
All Exercises from MODERN PUBLICATION Class 12 PHYSICS 15 MAGNETIC EFFECTS OF CURRENTS
- Multiple choice questions (Level - I)
- Multiple choice questions (Level - I) Paragraph questions
- Multiple choice questions (Level - I) Assertion and reasoning
- Multiple choice questions (Level - II)
- Multiple choice questions (Level - II) Paragraph questions
- Multiple choice questions (Level - III)
- Recent Competitive Questions