Complete Solutions to MCQ LEVEL- II of chapter WAVE OPTICS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | WAVE OPTICS |
| MODERN PUBLICATION | MCQ LEVEL- II |
| Number Of Questions | 33 |
| Academic Year | 2023-24 |
Unploarised light of intensity `I_(0)` falls on a Nicol prism.The light emerging from this Nicol Prism falls on another Nicol whose polarising axis is inclined to that of first by an ange `30^(@)`.The light emerginh from the second Nicol has the intensity:
View SolutionA Fresnel's biprism is used to form the interference fringes.The distance between the source and the biprism is 20 cms and that between the biprism and the screen is 80 cm. If ` lambda = 6563 Å` and the separation between the virtual sources is 3.6 mm, then the fringe width is :
View SolutionIn a Young's double slit experiment the fringes are displaced by a distance x when a glass plate of refractive index 1.5 is introduced in the path of one of the bemas.When this plate is replaced by another plate of the same thickness, the shift of fringes is `(3)/(2) x`.The refractive index of the second plate is :
View SolutionThe slits in Young's double slit experiment are 0.5 mm apart and interference pattern is observed on a screen distant 100 cm from the slits. It is found that the 9th bright fringe is at a distance of 8.835 mm. From the second dark fringe. The wavelength of light will be :
View SolutionAngular width of a central max is `30^(@)` when the slits is illuminated by light of wavelength `6000 Å`.Then width of the slit will be approx:
View SolutionIf velocity of a galaxy relative to earth is `1.2 xx 10^(6) ms^(-1)` then % increase in wavellenth of light from galaxy as compared to the similar source on earth will be :
View SolutionDoppler shift for the light of wavelength `6000 Å` emitted from the sun is `0.04 Å`.If radius of the sun is `7 xx 10^(8)` m then time period of rotation of the sun will be :
View SolutionOn itroducing a thin mica sheet of thickness `2 xx 10^(-6)` m and refractive index 1.5 in the path of one of the waves, central bright maxima shifts by n fringes.Wavelength of the wave ised is `5000 Å`, then n is :
View SolutionTwo beams of light having intensities I and 4I interfere to produce a fringe pattern on the screen.Phase differenced between the beams is `(pi)/(2)` at point A and `pi` at point B.Then difference between the resultant intensities at A and B is :
View SolutionA plane relectromagentic wave from of frequency `v_(0)` falls normally on the surfave of a mirror approaching with a relativistic velocity v. Then frequency of the reflected wave will be (given `beta= (v)/(c)`):
View SolutionA spectral line of wavelength 0.59 mm is observed in the directions to the opposite edges of the solar disc along its equator.A difference in wavelength equal to `(Delta lambda)`, 8 picometre is observed.Period of sun's revolution around its own axis will be about (Radius of sun = `6.95 xx 10^(8)`m)
View SolutionIn Young's double slit experiemnt using monochromatic light, fringe pattern shifts by a certain distance on the screen when a mica sheet of refractive index 1.6 and thickness 1.964 mm is introduced in the path of one of the twao waves.If now mica sheet is removed and distance between slit and screen is doubled, distance between successive max. or min. remains unchanged.The wavelength of the monochromatic light used in the experiment is :
View SolutionIn a Y oung's double slit experiment, separation between the slits is `2 xx 10^(-3)` m and distance of the screen from the slit is 2.5 m. Light in the range of 2000 - 8000 `Å` is allowed to fall on the slits.Wvelength in the visible region that will be present on the screen at `10^(-3)` m from the central maxima will be :
View Solution
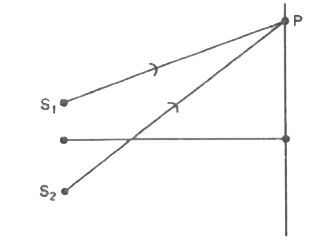
Fig. Shows two coherent sources `S_(1)` and `S_(2)`, emitting wavelength `lambda`.The separation `S_(1)S_(2) = 1.51. S_(1)` is ahead in phase by `(pi)/(2)` relative to `S_(2)`.The maxima occurs in a direction given by `sin^(-1)` of :
View SolutionIn a biprism experiment, the eye piece was palced at a distance of 20 cm from the source.The distance between two virtual sources was found to be 0.075 cm. Find the wavelength of source of light if the eye piece ahs to be moved through a distance of 1.888 cm for 20 fringes to cross the field of view :
View Solution80 g of impure sugar when dissolved in a litre of water gives an optical rotation of `9.9^(@)` when placed in a tube of length 20 cm.If the specific rotation of sugar is `66^(@)`, find percentage purity of sugar solution:
View SolutionIn Young's double slit experiment, the two slits act as coherent sources of equal amplitude A and of wavelength `lambda`.In another experiment with same set up, the two slits are sources of equal amplitude A and wavelength `lambda`, but are incoherent.The ratio of intensty of light at the mid - point of the screen in the first case to that in the second case is :
View SolutionThe distance between the slit and biprism and screen and biprism are 50 cm each.The obtuse angle of biprism is `179^(@)` and its refractive index is 1.5. If the distance between successive fringes is 0.135 mm, the wavelength of light used is :
View SolutionIn an interference pattern the path difference between waves starting from `S_(1)` and `S_(2)` and reaching at P is 1.5 microns i.e. `S_(2)P - S_(1)P = 1.5` microns. If the wavelength of light used be `6000 Å`, then the point P is :
View SolutionA slit of width d is placed in front of a lens of focal length `0.5 m` and is illuminated normally with light of wavelength `5.89 xx 10^(-7)`m. The first diffraction minima on either side of the central max. Are separated by `2 xx 10^(-3)`m. The width of the slit is :

View SolutionIn a double slit experiment using monochromatic light, the fringe patern shifts by a certain distance on the screen when a mica sheet of `mu = 1.6` and thickness `t = 1.964 mu m` is introduced in the path of the one of the interfering waves.The mica sheet is then removed and the distance between the slits and the screen is doubled.It is found that the distance between successive max. or min. is now the same as the observed fringe shift upon introducing of the mica sheet. Calculate the wavelength of light used in experiement:
View SolutionIn a biprism, 21 fringes are distinctly seen on screen at a distance of 1 m, when the sources are 0.5 mm apart, what is the coherent length and coherent time of the set up .(`lambda = 6000 Å`):
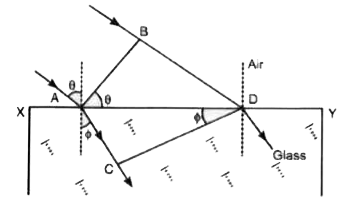
View SolutionA wavefront AB moving in air is incident on a plane glass surface XY as given in figure.Its position CD after refraction through the glass slab is shown along with normals A to D. The refractive index of glass w.r.t. Air will be equal to :
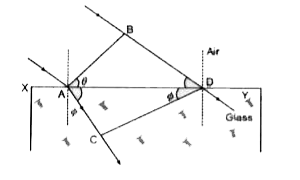
View SolutionA wavefront AB moving in air is incident on a plane glass surface XY as given in figure.Its position CD after refraction through the glass slab is shown along with normals A to D. The refractive index of glass w.r.t.air is given by :
View SolutionA broad source of light `lambda = 6800 Å` illumintates normally two glass plates 12 cm long. They touch at one end and are separated by a wire `0.048` mm. In diameter at the other end.How many bright fringes appear over the 12 cm. Distance.
View SolutionTwo coherent sources of intensity ratio `beta` interfere, the `(I_(max) - I_(min))/(I_(max) + I_(min))` is:
View SolutionTwo identical sources of light are separated through a distance `d = (lambda)/(8)`, where `lambda` is the wavelength of the waves emitted by either source. The phase difference of the sources is `(pi)/(4)`.Intensity distribution in the radiation field as a function of `theta` is :
View SolutionWhite light reflected at normal incidence from a soap film, has maximum at `6000 Å` and the minimum at `4500 Å` in the visible region with no minimum in between.If `mu = 1.33` for the film, the thickness of the film is :
View SolutionWhite light of spectral range 4000 - 7000 `Å` is incident normally on a soap film of uniform thickness 0.0004 mm and `mu = 1.3`. The wvaelengths of the light which are strongly reflected are :
View SolutionA ray of light of intensity I is incident on a parallel glass slab at a point A as shown.It undergoes partial reflection and refraction. At each reflection 25% of incident energy is reflected. The rays AB and A' B' undergo interference. The ratio `I_(max)/I_(min)` is :

View SolutionLight from a source emitting two wavelengths `lambda_(1)` and `lambda_(2)` is made tyo fall on Young's double slit appratus after filtering one of the wavelengths.The position of interference pattern is noted.When filter is removed, both the wavelength are incident.It is found that maximum intentsity is produced where the fourth maxima occured intially. If the other wvaelength is filtered, at the same location, the third maxima is found. What is the ratio of wavelengths?
View SolutionTwo light rays having the same wavelength `lambda` in vacuum are in phase initially. Then the first ray travels a path `L_(1)` through a medium of refractive index `n_(1)` while the second ray travels a path of length `L_(2)` through a medium of refractive index `n_(2)`. The two waves are then combined to observe interference. The phase difference between the two waves is :
View SolutionYoung's duble slit experiment is set up in a liquid.The 10th bright fringe in the liquid lies where the 6th dark fringe lies in vacuum. The refractive index of the liquid is approximately :
View Solution
MCQ LEVEL- II questions and complete solutions for chapter WAVE OPTICS of MODERN PUBLICATION PHYSICS (KANNADA ENGLISH) of Class 12