Complete Solutions to W.E. of chapter MOVING CHARGES AND MAGNETISM of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | MOVING CHARGES AND MAGNETISM |
| NARAYANA | W.E. |
| Number Of Questions | 61 |
| Academic Year | 2023-24 |
Eight wires cut the page perpendicular to the points shown. Each wire carries current `i_(0)`. Odd currents are out of the page and even current into the page. Find the line integral `ointvec(B).vec(dl)` along the loop.
View SolutionFind the magnetic induction due to a straight condutor of length `16cm` carrying current of `5A` at a distance of `6cm` from the midpoint of conductor.
View SolutionIf a straight conductor of length `40cm` bent in the form of a square and the current `2A` is allowed to pass through square, then find the magnetic induction at the centre of the square loop.
View SolutionIf a thin uniform wire of length `1m` is bent into an equilateral triangle and crries a current of `sqrt(2)A` in anticlockwise direction, find the net magnetic induction at the centroid
View SolutionA large straight current carrying conductor is bent in the form of `L` shape. Find `vec(B)` at `P`.
View SolutionInfinite number of straight wires each carrying current I are equally placed as shown in the figure Adjacent wires have current in opposite direction Net magnetic field at point `P` is
 .
.
View SolutionFind the magnetic field at `P` due to the arrangement shown
 .
.
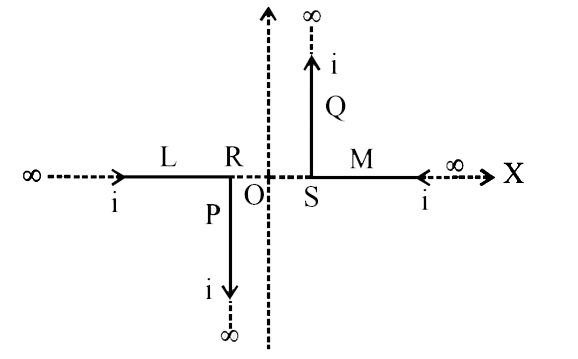
View SolutionA pair of stationary and infintely long bent wires are placed in the ` XY` planes as shown in fig. The wires carry currents of ` I = 10 amperes` each as shown . The segments `P and Q` are parallel to the ` Y-axis` such that ` OS = OR = 0.02 m`. Find the magnitude and direction of the magnetic induction at the origin `O`.
View SolutionAn equilateral triangle of side length `l` is formed from a piece of wire of uniform resistance. The current `I` is as shown in figure. Find the magnitude of the magnetic field at its centre `O`.

View SolutionA non - popular loop of conducting wire carrying a current `I` is placed as shown in the figure . Each of the straighrt sections of the loop is of the length ` 2a`. The magnetic field due to this loop at the point `P(a, 0 ,a)` points in the direction

View Solution`A 2A` current is flowing through a circular coil of radius `10 cm` containing `100 ` turns. Find the magnetic flux density at the centre of the coil.
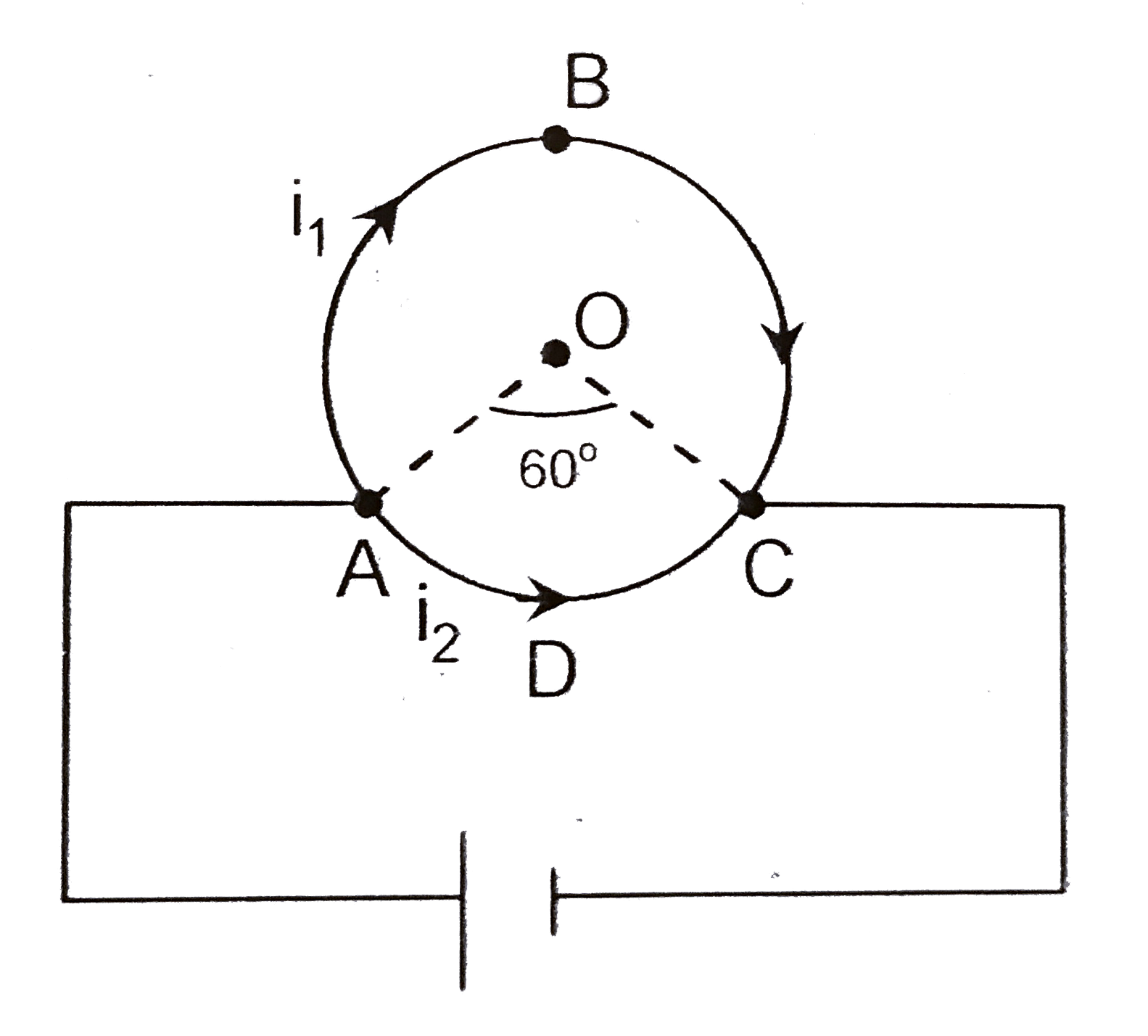
View SolutionA cell is connected between the point A and C of a circular conductor ABCD of centre `O, /_AOC = 60^(@)`. If `B_(1_` and `B_(2)` are the magnitude of magnetic fields at O due to the currents in ABC and ADC respectively, the ratio of `B_(1)//B_(2)` is.
View SolutionThree rings, each having equal radius R, are placed mutually perpendicular to each other and each having its centre at the origin of coordinate system. If current I is flowing through each ring, then the magnitude of the magnetic field at the common centre is

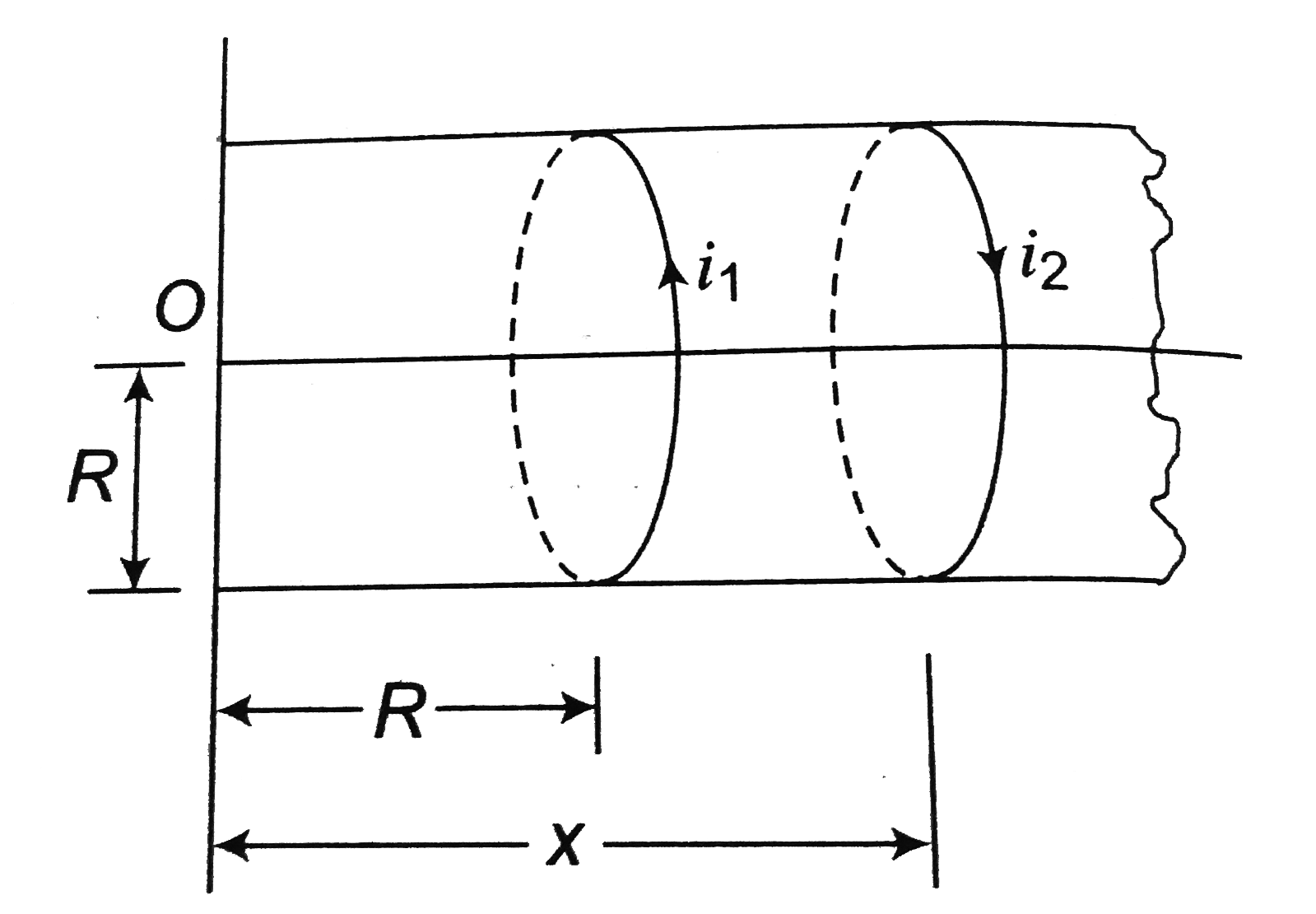
View SolutionTwo wires are wrapped over wooden cylinder to form two co-axial loops carrying currents `i_(1)` and `i_(2)`. If `i_(2)=8i_(1)` the value of `x` for `B=0` at the origin `O` is:
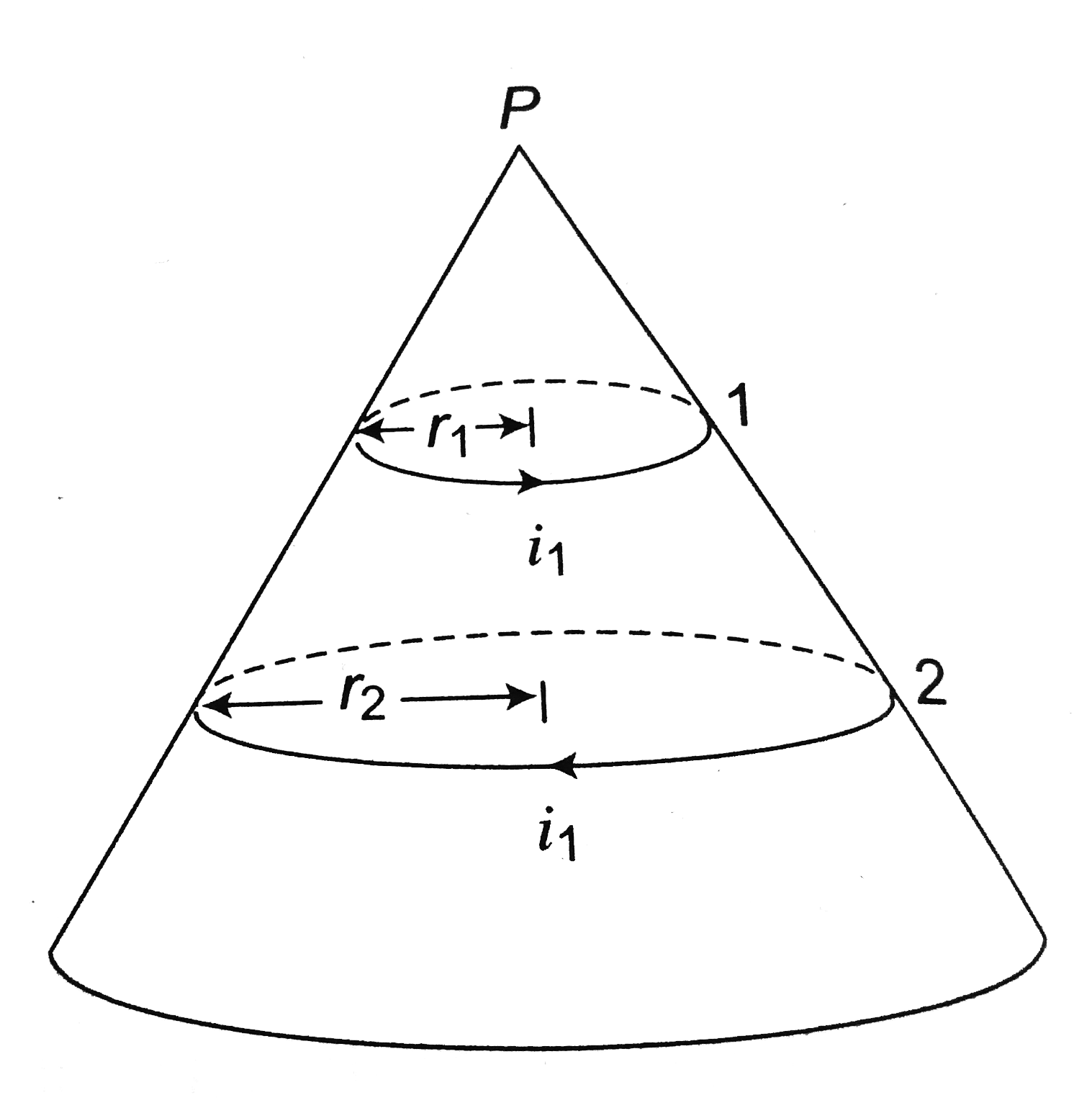
View SolutionTwo wires wrapped over a conical frame from the coils `1` and `2`. If they produce no net magnetic field at the apex `P`, the value of
View SolutionA thin insulated wire forms a plane spiral of `N=100` turns carrying a current `i=8mA`. The inner and outer radii are equal to `a=5 cm and b=10 cm`. Find the magnetic induction at the centre of the spiral

View SolutionA plastic disc of radius `'R'` has a charge `'q'` uniformly distributed over its surface. If the dis is rotated with a frequency `'f'` about its axis, then the magnetic induction at the centre of the disc is given by
View SolutionA charge of `1C` is placed at one end of a non conducting rod of length `0.6m`. The rod is rotated in a vertical plane about a horizontal axis passing through the other end of the rod with angular frequency `10^(4)pi rad//s.` Find the magnetic field at a point on the axis of rotation at a distance of `0.8m ` from the centre of the path.
View SolutionTwo circular coils made of same material having radii `20 cm & 30 cm` have turns `100 & 50` respectively. If they are connected `a )` in series `b)` in parallel `c)` separately across a source of ef find the ratio of magnetic inductions at the centre of circles in each case
View SolutionTwo circular coils are made from a uniform wire the ratio of radii of circular coils are `2:3 &` no. of turns is `3:4` . If they are connected in parallel across a battery.
`A:` Find ratio of magnetic inductions at their centres
`B:` Find the ratio magnetic moments of 2 coils.
View SolutionFigure shows a square current carrying loop `ABCD` of side `2m` and current` i=(1)/(2)A`. The magnetic moment `vec(M)` of the loop is

View SolutionIf two charged particles each of charge `q` mass `m ` are connected to the ends of a rigid massless rod and is rotated about an axid passing through the centre and `_|_` to length. Then find the ratio of magnetic moment to angular momentum.
View SolutionFind the magnetic dipole moment of the spiral of total number of turns`N`, carrying current `i` having inner and outer radii `a` and `b` respectively.

View SolutionConsider a non conducting plate of radius `a` and mass `m` which has a charge `q` distributed uniformly over it, The plate is rotated about its own axis with a angular speed `omega`. Show that the magnetic moment `M` and the angular momentum `L` of the plate are related as `(M)/(L)=(q)/(2m)`.
View SolutionA magnetic needle is arranged at the centre of a current carrying coil having 50 turns with radius of coil `20 cm` arranged along magnetic meridian. When a current of `0.5mA` is allowed to pass through the coil the deflection is observed to be `30^(@)`. Find the horizontal component of earth's magnetic field
View SolutionA solenoid of length `8 cm` has 100 turns in it. If radius of coil is `3 cm` and if it is carrying a current of `2A`, find the magnetic induction at a point `4 cm` from the end on the axis of the solenoid.
View SolutionA solenoid `60cm` long and of radius `4*0cm` has 3 layers of windings of `300` turns each. A `2*0cm` long wire of mass `2*5g` lies inside the solenoid (near its centre) normal to the axis : both the wire and the axis of the solenoid are in the horizontal plane. The wire is connected through two leads parallel to the axis of solenoid to an external battery which supplies a current of `6*0A` in the wire. What value of current (with appropriate sense of circulation) in the windings of the solenoid can support the weight of the wire? `g=9*8ms^-2`.
View SolutionA toroid of non ferromagnetic has core of inner radius `25cm` and outer radius `26cm`. It has 3500 turns `&` carries a current of `11A`, then find the magnetic field at a point
`(i)` In the internal cavity of toroid
`(ii)` At the midpoint of the windings
`(iii)` At a point which is at a distance of `30cm` from the centred of toroid.
View SolutionA solenoid of `2m` long `& 3 cm` diameter has 5 layers of winding of 500 turns per metre length in each layer `&` carries a current of `5A`. Find intensity of magnetic field at the centre of the solenoid.
View SolutionA magnetic field of `(4.0xx10^-3hatk)T` exerts a force `(4.0hati+3.0hatj)xx10^-10N` on a particle having a charge `10^-9C` and moving in te `x-y` plane. Find the velocity of the particle.
View SolutionIf a particle of charge `1 muC` is projected into a magnetic fiels `vec(B)=(2hat(i)+yhat(j)-zhat(k))T` with `a` velocity `vec(V)(4hat(i)+2hat(j)-6hat(k))ms^(-1)`, then it passes undeviated. If it is now projected with a velocity `vec(V)=hat(i)+hat(j)`, then find the force experienced by it
View SolutionAn `alpha-`particle is accelerated by a potential difference of `10^4 V.` Find the change in its direction of motion, if it enters normally in a region of thickness 0.1 m having transverse magnetic induction of 0.1 tesla. (Given: mass of `alpha-`particle `6.4xx10^(-27)`kg).
View SolutionThe magnetic field is confirmed in a square region. A positive charged particle of charge q and mass m the limiting velocities of the particles so that it may come out of face (1), (2), (3), and (4).

View SolutionA particle of mass m and charge +q enters a region of magnetic field with a velocity v, as shown in Fig. 1.93.
a. Find the angle subtended by the circular arc described by it in the magnetic field.
b. How long does the particle stay inside the magnetic field?
c. If the particle enters at E, what is the intercept EF?

View SolutionFind the force experienced by the wire carrying a current `2A` if the ends `P` and `Q` of the wire have coordinates `(1,2-3)m` and `(-2,-5,1)m` respectively when it is placed in a magnetic field `vec(B)=(hat(i)+hat(j)+hat(k))T`
View SolutionIn the figure shown a semicircular wire loop is placed in a uniform magnetic field `B=1.0T`. The plane of the loop is perpendicular to the magnetic field. Current `i=2A` flows in the loop in the directions shown. Find the magnitude of the magnetic force in both the cases `a` and `b`. The radius of the loop is 1.0 m

View SolutionA rough inclined plane inclined at angle of `37^(@)` with horizontal has a metallic wire of length `20cm` with its length `_|_` to length of inclines plane `(mu=0.1)` When a current of its passingthrough the wire and a magnetic field is applied normal to the plane upwards, the wire starts moving up with uniform velocity for `B=0.5T`. The find the magnitude of current `i,(` mass of the wire `=50g)`
View SolutionA matel wire PQ of mass 10g lies at rest on two horizontal metal rails separated by 4.90 cm . A vertically downward magnetic field of magnitude 0.800 T exists in the space. The resistance of the circuit is slowly decreased and it is found that when the resistance goes below`20.0 Omega`, the wire PQ starts sliding on the rails. Find the coefficient of friction.

View SolutionA current carrying conductor of mass `m`, length `1 ` carrying a current `i` hangs by two identical springs each of stiffness `k`. For an outward magnetic field `B` find the deformation of the springs. Put `m=50gm.g=10m//s^(2),l=1//2m,i=1A` and `B=1T` and `k=50N//m`

View SolutionA square loop of side a hangs from an insulating hanger of spring balance. The magnetic field of strength `B` occurs only at the lower edge. It carries a current `I` . Find the change in the reading of the spring balance if the direction of current is reversed.

View SolutionA rod `CD` of length `b` carrying a current `I_(2)` is placed in a magentic field due to a thin long wire `AB` carrying current `I_(1)` as shown in figure. Then find the net force experience by the wire
View SolutionA long straight conductor carrying a current of `2A` is in parallel to another conductor of length `5 cm`. And carrying a current `3A`. They are separated by a distance of `10 cm`. Calculate `(a)B` due to first conductor at second conductor `(b)` the force on the short conductor.
View SolutionTwo long straight parallel current carrying conductors each of length `l` and current `i` are placed at a distance `r_(0)`. Show that the total work done by an external agent in slowly reducing their distance of separation to `(r_(0))/(2)` is `(mu_(0))/(2pi)i^(2)ln(2)`
View SolutionTwo parallel horizontal conductors are suspended by two light vertical threads each 75 cm long. Each conductor has a mass of `40gm`, and when there is no current they are 0.5 cm apart. Equal current in the two wires result in a separation of 1.5 cm. Find the values and directions of currents. Take `g=9.8ms^-2`.
View SolutionA conductor `AB` of length `10 cm` at a distance of `10cm` from an infinitely long parallel conductor carrying a current `10A` . What work must be done to move `AB` to a distance of `20cm` if it carries `5A` ?
View SolutionThree long straight wires are connected parallel to each other across a battery of negligible internal resistance. The ratio of their resistances are `3:4:5`. What is the ratio of distances of middle wire from the others if the net forces experienced by it is zero.
View SolutionA circular loop of area `1 cm^(2)` carrying a current of `10A` is placed in a magnetic field of `2That(i)`. The loop is in `xy` plane with current in clockwise direction . Fing the torque on the loop
View SolutionA metallic wire is folded to form a square loop a side `'a'`. It carries a current `'I'` and is kept perpendicular to a uniform magnetic field. If the shape of the loop is changed from square to a circle without changing the length of thw wire and current, the amount of work done in doing so is
View SolutionA flat insulating disc of radius `'a'` carries an excess charge on its surface is of surface charge density `sigma C//m^(2)`. Consider disc to rotate around the perpendicular to its plane with angular speed `omega rad//s`/ If magnetic field `vec(B)` is directed perpendicular to the roation axis, then find the torque acting on the disc.
View SolutionA loop, carring a current i, lying in the plane of the paper, is in the field of a long straight wire with current `i_0` (inward) as shown in Fig. Find the torque acting on the loop.

View SolutionThe area of the coil in a moving coil galvanometer is `15cm^(2)` and has 20 turns. The magnetic induction is `0.2T` and the couple per unit twist of the suspended wire is `10^(-6) Nm` per degree. If the deflection is `45^(@)`, the current passing through it is
View SolutionA coil of area `100cm^(2)` having 500 turns carries a current of `1mA` . It is suspended in a uniform magnetic field of induction `10^(-3)wb//m^(2)` . Its plane makes an angle fo `60^(@)` with the lines of induction. The torque acting on the coil is
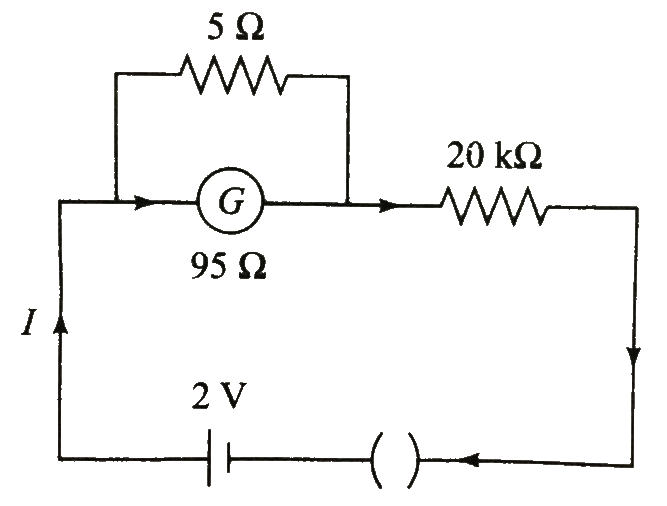
View SolutionA galvanometer of resistance `95 Omega`, shunted resistance of `5 Omega`, gives a deflection of `50` divisions when joined in series with a resistance of `20 k Omega` and a `2 V` accumulator. What is the current sensitivity of the galvanomter (in div`//mu A`)?
View SolutionA galvanometer of resistance `20Omega` is shunted by a `2 Omega` resistor. What part of the main current flows through the galvanometer ?
View SolutionA galvanometer has resistance `500 ohm`. It is shunted so that its senstivity decreases by 100 times. Find the shunt resistance.
View SolutionThe resistance of galvanometer is `999Omega`. A shunt of `1 Omega` is connected to it.If the main current current is `10^(-2)A`, what is the current flowing through the galvanometer .
View SolutionA galvanometer has a resistance of `98Omega`. If `2%` of the main current is to be passed through the meter, what should be the value of the shunt ?
View SolutionA maximum current point `0.5mA` can be passed through a galvanometer of resistance `20Omega` . The resistance to be connected in series to convert it in the voltmeter of range `0-5V` is
View SolutionA galvanometer has a resistance of `100Omega`. A current of `10^(-3)` A pass through the galvanometer How can it be converted into `(A)` ammeter of range `10A` and `(b)` voltmeter of range `10v`
View SolutionA galvanometer having `30` divisions has a current sensitivity of `20muA//di vision`. It has a resistance of `25Omega`. How will you convert it into an ammeter upto 1 ampere? How will you convert this ammeter into a voltmeter up to 1 volt?
View SolutionWhat is the value of the shunt that passes `10%` of the main current through a galvenomenter of `99 Omega`?
View Solution
W.E. questions and complete solutions for chapter MOVING CHARGES AND MAGNETISM of NARAYANA PHYSICS (HINGLISH) of Class 12
All Exercises from NARAYANA Class 12 PHYSICS MOVING CHARGES AND MAGNETISM
- C.U.Q (AMPERE.S CIRCUITAL LAW MAGNETIC FIELD DUE TO STRAIGHT CONDUCTOR )
- C.U.Q (CONVERSION OF MCG INTO AMMETER)
- C.U.Q (CONVERSION OF MCG INTO VOLTMETER)
- C.U.Q (CURRENT LOOP AND MAGNETIC DIPOLE)
- C.U.Q (FORCE BETWEEN TWO PARALLEL CURRENT CARRYING CONDUCTORS)
- C.U.Q (FORCE ON A MOVING CHARGE IN MAGNETIC FIELD)
- C.U.Q (FORCE ON A CURRENT CARRYING CONDUCTOR IN A MAGNETIC FIELD)
- C.U.Q (MOVING COIL GALVANOMETER)
- C.U.Q (TANGENT GALVANOMETER)
- C.U.Q (TORQUE ON CURRENT LOOP)
- C.U.Q-KEY
- EXERCISE - 1(C.W) (AMPERE.S CIRCUITAL LAW BIOT-SAVART LAW AND ITS APPLICATIONS)
- EXERCISE - 1(C.W) (CONVERSION OF MCG INTO AMMETER AND VOLTMETER)
- EXERCISE - 1(C.W) (CURRENT LOOP AND MAGNETIC DIPOLE)
- EXERCISE - 1(C.W) (CYCLOTRON)
- EXERCISE - 1(C.W) (FORCE ACTING A MOVING CHARGE IN MAGNETIC FIELD)
- EXERCISE - 1(C.W) (FORCE BETWEEN TWO PARALLEL CURRENT CARRYING CONDUCTORS)
- EXERCISE - 1(C.W) (FORCE ON A CURRENT CARRYING CONDUCTOR IN A MAGNETIC FIELD)
- EXERCISE - 1(C.W) (MOVING COIL GALVANOMETER)
- EXERCISE - 1(C.W) (SOLENOID AND TOROID)
- EXERCISE - 1(C.W) (TANGENT GALVANOMETER)
- EXERCISE - 1(C.W) (TORQUE ON CURRENT LOOP)
- EXERCISE - 1(H.W) (AMPERE.S CIRCUITAL LAW BIOT-SAVART LAW AND ITS APPLICATIONS
- EXERCISE - 1(H.W) (CONVERSION OF MCG INTO AMMETER AND VOLTMETER)
- EXERCISE - 1(H.W) (CYCLOTRON)
- EXERCISE - 1(H.W) (FORCE ACTING ON A MOVING CHARGE IN MAGNETIC FIELD)
- EXERCISE - 1(H.W) (FORCE BETWEEN TWO PARALLEL CURRENT CARRYING CONDUCTORS)
- EXERCISE - 1(H.W) (FORCE ON CURRENT CARRYING CONDUCTOR IN A MAGNETIC FIELD)
- EXERCISE - 1(H.W) (MOVING COIL GALVANOMETER)
- EXERCISE - 1(H.W) (SOLENOID AND TOROID)
- EXERCISE - 1(H.W) (TORQUE ON CURRENT LOOP)
- EXERCISE - 2(C.W) (AMPERE.S CIRCUITAL LAW BIO-SAVART LAW AND ITS APPLICATIONS)
- EXERCISE - 2(C.W) (CONVERSION OF MCG INTO AMMETER AND VOLTMETER)
- EXERCISE - 2(C.W) (CURRENT LOOP AND MAGNETIC DIPOLE)
- EXERCISE - 2(C.W) (FORCE ACTING ON A MOVING CHARGE IN MAGNETIC FIELD)
- EXERCISE - 2(C.W) (FORCE BETWEEN TWO PARALLEL CURRENT CARRYING CONDUCTORS)
- EXERCISE - 2(C.W) (MOVING COIL GALVANOMETER)
- EXERCISE - 2(C.W) (SOLENOID AND TOROID)
- EXERCISE - 2(C.W) (TANGENT GALVANOMETER)
- EXERCISE - 2(C.W) (TORQUE ON CURRENT LOOP)
- EXERCISE - 2(H.W) (AMPERE.S CIRCUITAL LAW BIO-SAVART LAW AND ITS APPLICATIONS)
- EXERCISE - 2(H.W) (CURRENT LOOP AND MAGNETIC DIPOLE)
- EXERCISE - 2(H.W) (FORCE ACTING A MOVING CHARGE IN MAGNETIC FIELD)
- EXERCISE - 2(H.W) (SOLENOID AND TOROID)
- EXERCISE - 2(H.W) (TANGENT GALVANOMETER)
- EXERCISE - 3
- EXERCISE - 4
- ILLUSTRATION
- Level -II (H.W)
- Level =I (H.W)
- LEVEL-I(C.W)
- Level-II(C.W)
- LEVEL-III
- LEVEL-V (SINGLE ANSWER QUESTION)
- LEVEL-VI (SINGLE ANSWER QUESTION)
- NCERT Based Questions
- W.E.