Complete Solutions to LEVEL-V (SINGLE ANSWER QUESTION) of chapter MOVING CHARGES AND MAGNETISM of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | MOVING CHARGES AND MAGNETISM |
| NARAYANA | LEVEL-V (SINGLE ANSWER QUESTION) |
| Number Of Questions | 85 |
| Academic Year | 2023-24 |
Two infinitely long, thin, insulated, straight wires lie in the x-y plane along the x- and y- axis respectively. Each wire carries a current I, respectively in the positive x-direction and positive y-direction. The magnetic field will be zero at all points on the straight line:
View SolutionIn the given figure the magnitude of magnetic field at `O` is ( all three wires are quarter circular ares )

View SolutionTwo parallel, long wires carry current `i_(1)` and `i_(2)` with`i_(1)gti_(2)`. When the currents are in the same direction, the magnetic field at a point midway between the wires is `30 muT`. If the direction of `i_(1)` is reversed , the field becomes `90muT`. The ratio `i_(1)//i_(2)` is
View SolutionMagnetic field `B` along the axis of a long solenoid is given by
View SolutionThe magnetic field at the centre `O` of the circular portion of radius `3 cm` carrying current 4 ampere in the wire is

View SolutionAn infinitely long conductor ` PQR` is bent to form a light angle as shown in Figure . A current `I` flows through `PQR` . The magnetic field due to this current at the point `M` is `H_(1)`. Now , another infinitely long straight conductor `QS` is connected at `Q` so that current is `(I)/(2)` in `QR` as well as in `QS` , the current in `PQ` remaining unchanged . The magnetic field at `M` is now `H_(2)`. The ratio `(H_(1))/(H_(2)` is given by
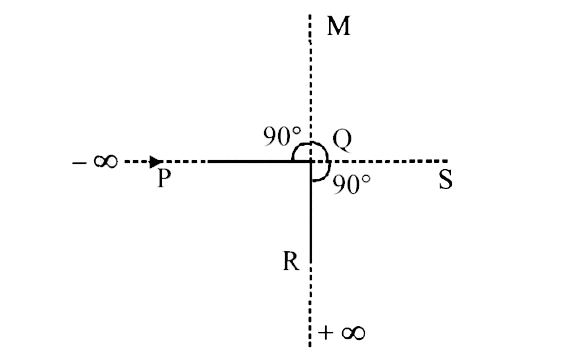
View SolutionA long current wire is bent in the shapes shown in figure. The circular portion has radius `R`. The magnetic induction at the center of the circular segment is

View SolutionAn ionized gas contains both positive and negative ions . If it is subjected simultaneously to an electric field along the ` +x` - direction and a magnetic field along the ` +y` - direction and the negative ions towardws `-y` - direction
View SolutionA charged particle is released from rest in a region of steady and uniform electric and magnetic fields which are parallel to each other . The particle will remove in a
View SolutionA charged particle of mass `m` and charge `q` enters a magnetic field `B` with a velocity `v` at an angle `theta` with the direction of `B`. The radius fo the resulting path is
View SolutionA particle of mass `m` and charge `q` is projected into a region having a perpendicular magnetic, field `B`. Find the angle of deviation of the particle as it comes out of the magnetic field if th,, width of the region is (b)
(a) `(2mv)/(Bq) (b) `(mv)/(Bq)` (c) `(mv)/(2 Bq)`
View SolutionA charged particle having charge `10^-6` C and mass of `10^-10` kg is fired from the middle of the plate making an angle `30^@` with plane of the plate. Length of the plate is `0.17 m` and it is separated by `0.1 m`. Electric field `E = 10^-3N/C` is present between the plates. Just outside the plates magnetic field is present. Find the velocity of projection of charged particle and magnitude of the magnetic field perpendicular to the plane of the figure, if it has to graze the plate at C and A parallel to the surface of the plate. (Neglect gravity)

View SolutionA particle moves in a circle of diamater 1.0 cm under the action of magnetic field of 0.40 T, An electric field of `200 V m^(-1)` makes the path straight. Find the charges/mass ration of the particle.
View SolutionA proton , a deutron and `alpha )`- particle having the same kinetic energy are moving in circular trajectories in a constant magnetic field . If ` r_(p), r_(d) , and r_(alpha)` denote respectively the radii of the trajectories of these particles , then
View SolutionA proton of mass `1.67xx10^(-27)kg` and charge `1.6xx10^(-19)c` is projected with a speed of `2xx10^(6)m//s` at an angle of `60^(@)` to the x-axis. If a uniform magnetic field of `0.104` Tesla is applied along Y-axis, the path of proton is
View SolutionFor a positively charged particle moving in a `x-y` plane initially along the `x-axis` , there is a sudden change in its path due to the presence of electric and//or magnetic fields beyond `p` . The curved path is shown in the ` x- y `plane and is found to be non - circular. Which one of the following combinations is possible ?
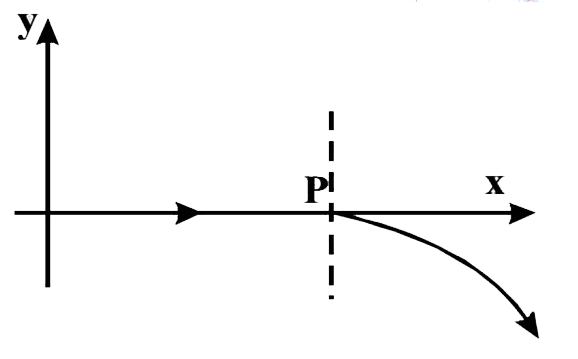
View SolutionAn electron moving with a speed u along the positive x-axis at `y=0` enters a region of uniform magnetic field which exists to the right of y-axis. The electron exits from the region after some time with the speed v at coordinate y, then

View SolutionA uniform magnetic field is directed out of the page. A charged particle , moving in the plane of the page, follows a clockwise spiral of decreasing radius as shown. A reasonable explanation is `:`

View SolutionThere is a horizontal cylindrical uniform but time-varying nagnetic field increasing at a constant rate `dB//dt` as shown in Fig. 3.173. A charged particle having charge `q` and mass `m` is kept in euilibrium, at the top of a spring of spring constant `K`, in such a way that it is on the horizontal line passing through the center of the magnetic field as shown in the figure. The compression in the spring will be

View SolutionA charged particle of specific charge (charge/mass) `alpha` released from origin at time `t=0` with velocity `vec v = v_0 (hat i + hat j)` in uniform magnetic field `vec B = B_0 hat i.` Coordinates of the particle at time `t= pi//(B_0 alpha)` are
View SolutionConsider the uniform magnetic field shown:

Starting from point P and without leaving the region of magnetic field, is it possible to choose a closed path (that is, a path that returns to P) for which the line integral of the magnetic field is nonzero?
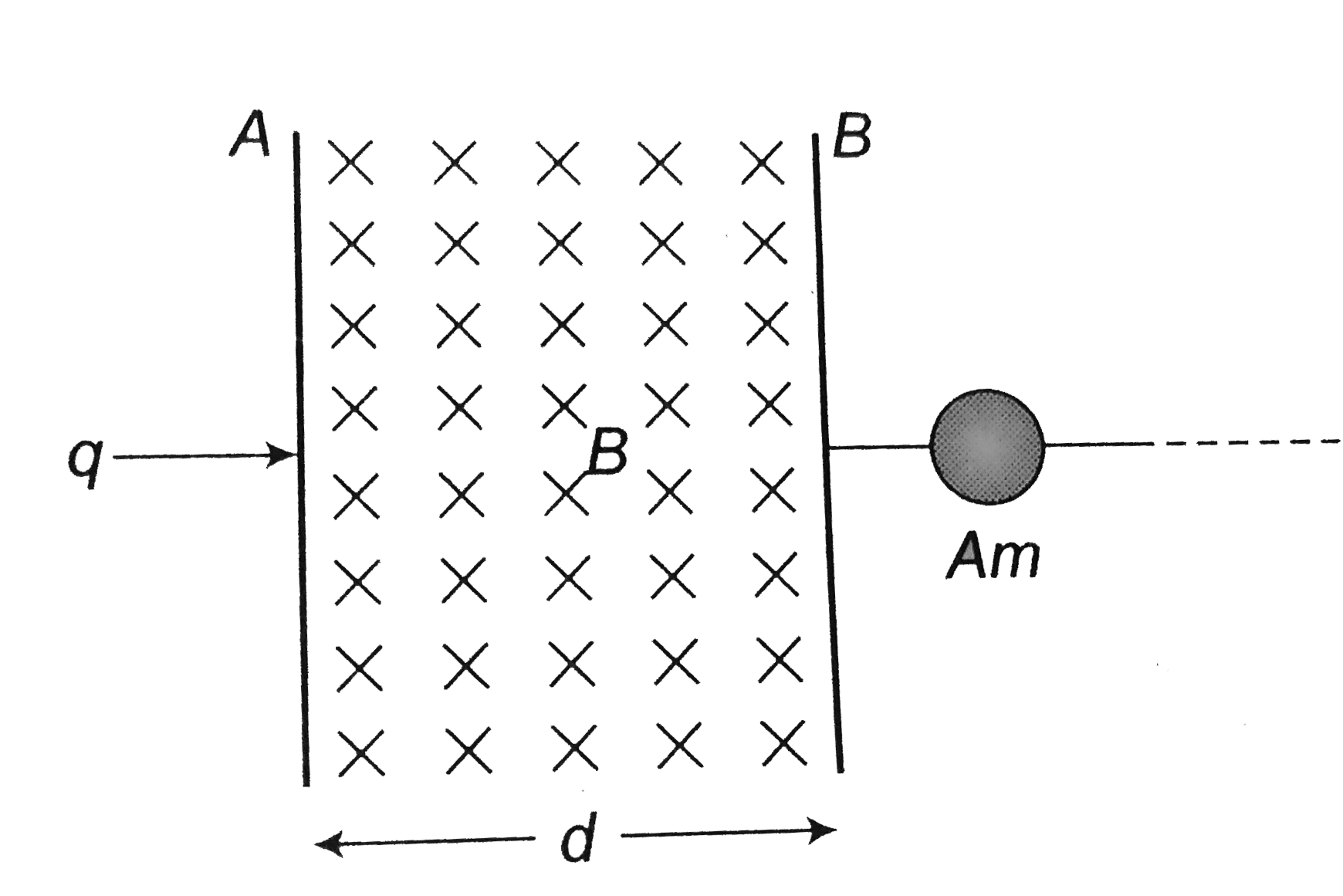
View SolutionTwo charged plates `A` and `B` are at the same electrical potential, and parallel and separated by a distance `d.` A unifrom magnetic induction field `B` acts perpendicular to plane of paper (and parallel to plates)n between the plates. Particels,each with charge `q`, mass `m` and kinetic energy `K` are shot throgh a hole in `A` directly towards `B`, each particle entering the hole perpendicular to `A`, An ammeter `AM` connected to an electrical network is connected to `B` and measures the current collected by the plate `B`, as the particles hit it. The limited value of the fied `B` for which the ammeter will stop showing a current is
View SolutionA particle of charge per unit mass `alpha` is released from origin with a velocity `vecv=v_(0)hati` in a magnetic field
`vec(B)=-B_(0)hatk` for `xle(sqrt(3))/2 (v_(0))/(B_(0)alpha)`
and `vec(B)=0` for `xgt(sqrt(3))/2 (v_(0))/(B_(0)alpha)`
The `x`-coordinate of the particle at time `t((pi)/(3B_(0)alpha))` would be
View SolutionA conducting loop carrying a current `I` is placed in a uniform magnetic field ponting into the plane of the paper as shown. The loop will have a tendency to

View SolutionTwo thin long parallel wires seperated by a distance 'b' are carrying a current ' I' amp each . The magnitude of the force3 per unit length exerted by one wire on the other is
View SolutionA rod of mass `m` and radius `R` rest on two parallel rails that are distance `l` apart and have a length `L`. The rod carries a current `I`( in the direction shown ) and rolls along the rails without slipping. A uniform magnetic field `B` is directed perpendicular to the rod and the rails. If it starts from rest, wat is the speed of the rod as it leaves the rails ?

View SolutionTwo long conducting rods suspended by means of two insulating threads as shown in Fig. are connected at one end to a charged capacitor through a switch S, which initially open. At the other end , they are connected by a loose wire. The capacitor has charge Q and mass per unit length of the rod is `lambda`. The effective resistance of the circuit after closing the switch is R. Find the velocity of each rod when the capacitor is discharged after closing the switch. (Assume that the displacement of rods during the discharging time is negligible.)

View SolutionA straight peice of conducting wire with mass M and length L is placed on a frictionless incline tilited at an angle `theta` from the horizontal (as shown in fig) There is a uniform. Vertical magnetic field at all points (produced by an arrangement of magnets not shown in fig. To keep the wire from sliding down the incline, a voltage source is

attached to the ends of the wire. When just the right amount of current flows through the wire, the wire remains at rest. Determine the magnitude and direction of the current in the wire that will cause the wire to remain at rest.
View SolutionFigure shows four wires placed in the same uniform magnetic field `B` and carrying the same current in which case force acting on the wire is minimum
View SolutionAn alpha particle moving with a velocity `vec(v)_(1)=2hat(i)m//s` is a uniform magnetic field experiences a force `vec(F)_(1)=-4e(hat(j)-hat(k))N`. When the particle moves with a velocity `vec(v)_(2)=hat(j)m//s`, then the force experienced by it is `vec(F)_(2)=2e(hat(i)-hat(k))N`. The magnetic induction `vec(B)` at that point is `:`
View SolutionA non-conducting rod having circular cross section of radius R is suspended from a rigid support as shown in fig. A light and small coil of 300turns is wrapped tightly at the left end where uniform magnetic filed B exists in vertically downward direction. Air of density `rho` hits the half of the right part of the rod with velocity V as shown in the fig. What should be current in clockwise direction (as seen from O) in the coil so that rod remains horizontal? Give answer in mA. Given `2/(Lv)sqrt((piRB)/(rho))=1/(sqrt5)A^(-1//2)`.
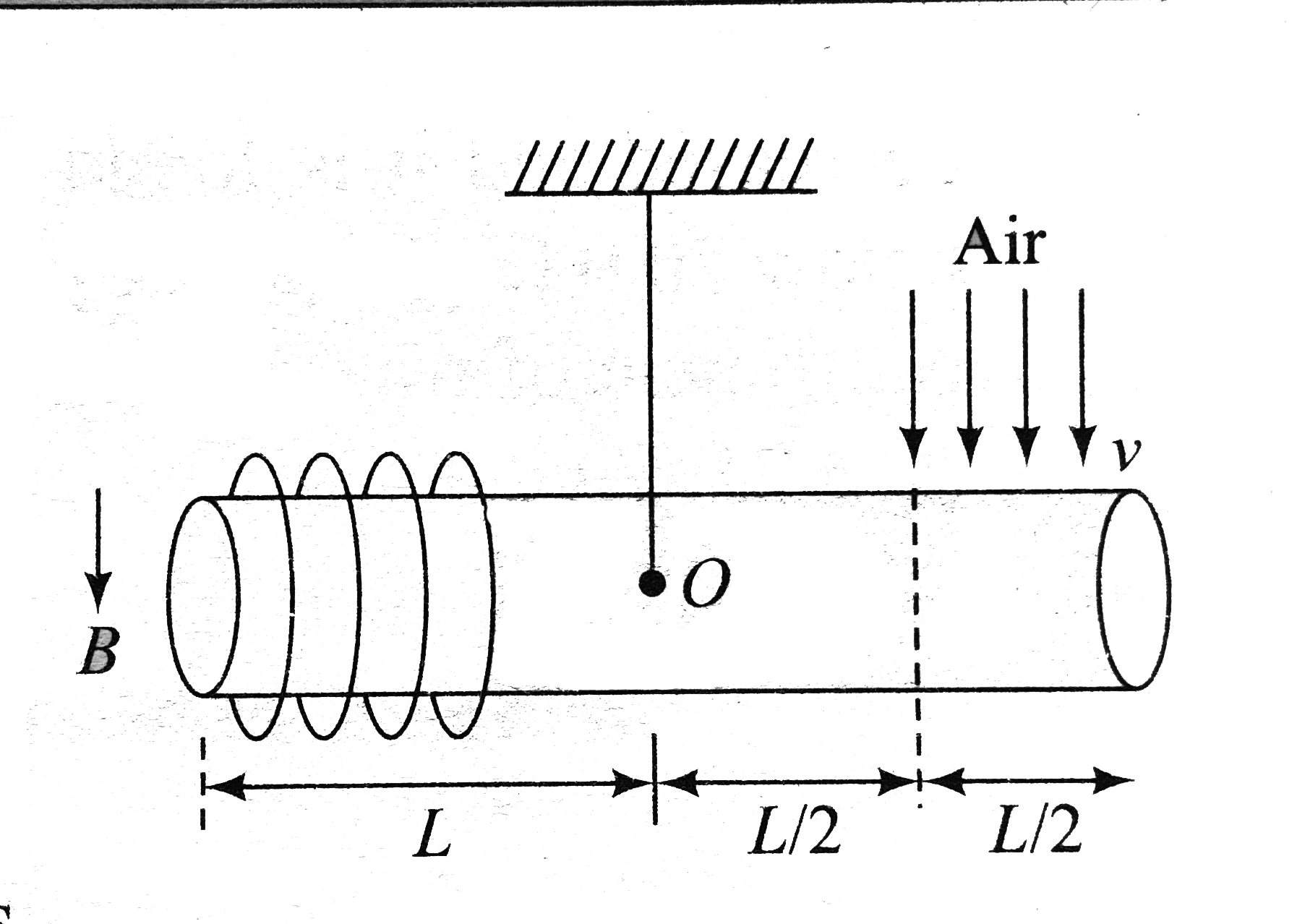
View SolutionA current carrying wire frame is in the shape of digit eight `(8)`. It is carrying current `i_(0)`. If the radius of each loop is `R_(0)`, then the net magnetic dipole moment of the figure is `:`

View SolutionAn insulating rod of length I carries a charge q distrubuted uniformly on it. The rod is pivoted at its mid-point and is rotated at a frequency f about a fixed axis perpendicular to the the rod and passing through the pivot . The magnetic moment of the rod system is
View SolutionQ charge is uniformaly distributed over the same surface of a right circular cone of semi -vertical angle theta and height h The cone is uniformly rotated about its axis at angular velocity omega Calculated associated magnetic dipole moment
 .
.
View SolutionA sphere of radius R, uniformly charged with the surface charge density `sigma` rotates around the axis passing through its centre at an angular velocity. (a) Find the magnetic induction at the centre of the rotating sphere. (b) Also, find its magnetic moment.
View SolutionA conductor carries a constant current I along the closed path abcdefgha involving 8 of the 12 edges of length `l`. Find the magnetic dipole moment of the closed path.
View SolutionTwo insulated rings, one of a slighlty smaller diameter than the other are suspended along their common diameter as shown. Initially the planes of the rings are mutually perpendicular. When a steady current is set up each of them
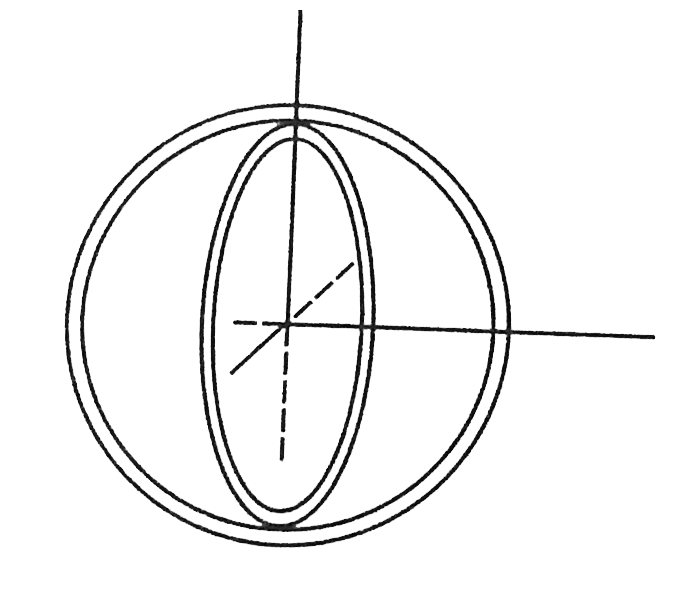
View SolutionA uniformly charged ring of radius `R` is rotated about its axis with constant linear speed `v` of each of its particle. The ratio of electric field to magnetic field at a point `P` on the axis of the ring distant `x=R` from centre of ring is `( c` is speed of light )

View SolutionIn the given loop length of each side is `a`. Current flowing through the loop is `I=1` amp. Find its manetic dipole moment.

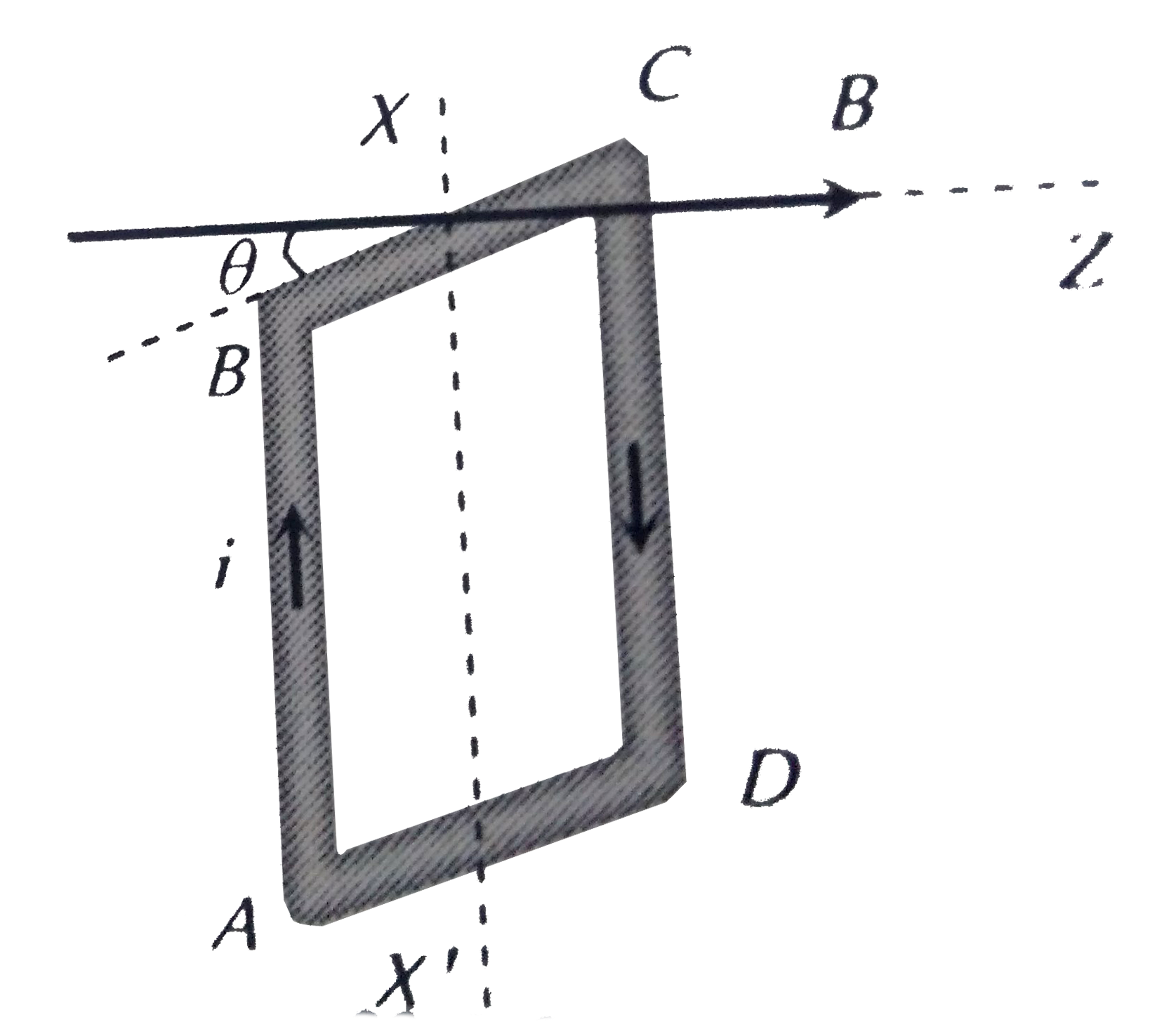
View SolutionThe square loop `ABCD`, carrying a current `i`, is placed in uniform magnetic field `B`, as shown. The loop can rotate about the axis `XX'`. The plane of the loop makes and angle`theta(theta lt 90^(@))` with the direction of `B`. Through what angle will the loop rotate by itself before the torque on it becomes zero
View SolutionA flat circular coil, carrying a current, has a magnetic moment `mu`
View SolutionA current ` I` flows along the length of an infinitely long, straight , thin - walled pipe. Then
View SolutionA long straight conductor carrying a current `i` is bent to form an almost complete circular loop of radius `r` on it. The magnetic field at the centre of the loop

View SolutionThe figure shows an infinitely long current wire out of the plane of the paper ( shown as a dot `'o.'`). A current carrying loop ABCD is placed as shown in figure. The loop

View SolutionA charged particle moves in a uniform magnetic field. The velocity of the particle at some instant makes an acute angle with the magnetic field. The path of the particle will be
View SolutionA charged particle goes undeflected in a region containing electric and magnetic field. It is possible that
(i) `vec(E) || vec(B). vec(v) || vec(E)`
(ii) `vec(E)` is not parallel to `vec(B)`
(iii) `vec(v) || vec(B)` but `vec(E)` is not parallel to `vec(B)`
(iv) `vec(E)||vec(B)` but `vec(v)` is not parallel to `vec(E)`
View SolutionA region has uniform electric and magnetic fields along the positive `x`-direction. An electron is fired from the origin at an angle `theta( lt 90^(@))` with the x-axis. It will
(i) move along a helical path of increasing pitch
(ii) move along a helical path of decreasing pitch initially
(iii) return to the `yz` plane at some time
(iv) come to rest momentarily at some position
View SolutionA semicircular wire of radius `r`, carrying a current `I`, is placed in a magnetic field of magnitude `B`. The force acting on it
View SolutionA charged particle of unit mass and unit charge moves with velocity `vecv=(8hati+6hatj)ms^-1` in magnetic field of `vecB=2hatkT`. Choose the correct alternative (s).
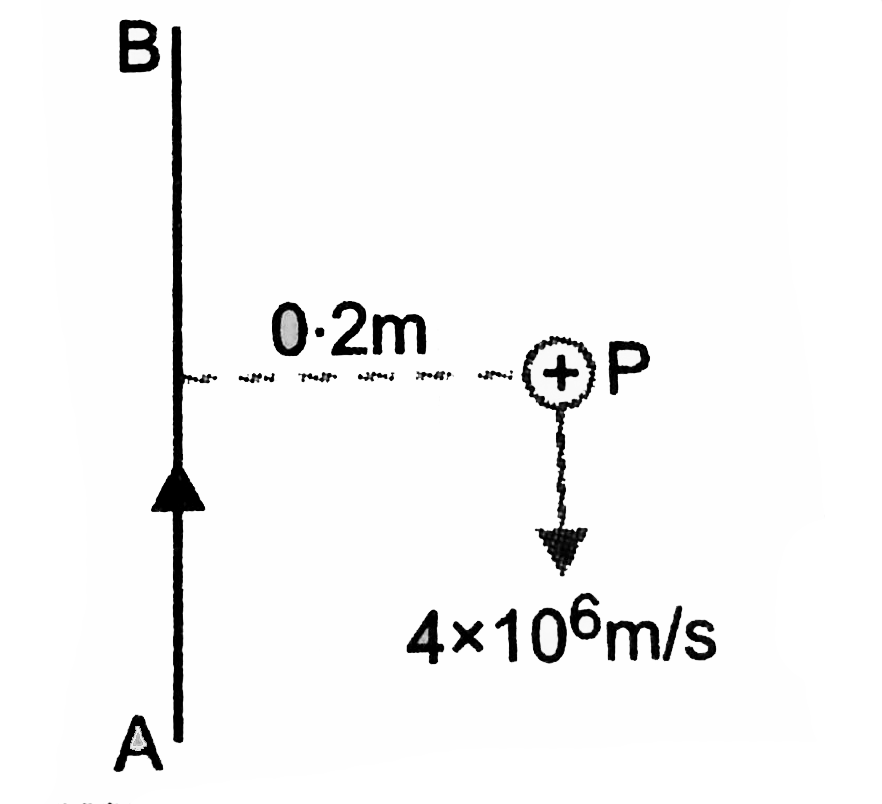
View SolutionA long straight wire AB carries a current of `4A`. A proton P travels at `4xx10^6ms^-1` parallel to the wire, `0*2m` from it and in a direction opposite to the current as shown in figure. Calculate the force which the magnetic field of current exerts on the proton. Also specify the direction of the force.
View SolutionTwo circular coil of radii 5cm and 10cm carry equal currents of 2A. The coils have 50 and 100 turns, respectively, and are placed in such a way that their planes as well as their centers coincide. Magnitude of magnetic field at the common centre of coils is
View SolutionTwo long thin, parallel conductors carrying equal current in the same direction are fixed parallel to the x-axis one passing through magnetic field due to the two conductors at any point is `B` Which of the following are correct ?(A) B=0 for all points on the x-axis (B) At all points on the y-axis, excluding the origin, B has only a zcomponent. (C) At all points on the z-axis, excluding the origin, B has only an x-component.

View SolutionA long straight wire carries the current along +ve x-direction. Consider four points in space `A(0,1,0), B(0,1,1), C(1,0,1), and D(1,1,1)`. Which of the pairs will have the same magnitude of magnetic field?
View SolutionCurrent flows through a straight cylindrical conductor of radius r. The current is distributed uniformly over its cross-section. The magnetic field at a distanace x from the axis of the conductor has magnitude B:
View SolutionThere are two infinite parallel current carrying wires in vertical plane. Lower wire is fixed and upper wire is having a linear mass density `lambda`. Two wires are carrying currents `I_(1)` and `I_(2)`. Now upper wire is placed in a magnetic field produced by lower wire. Magnetic field due to lower wire at the location of upper wire is `(mu_(0)I)/(2pid)`, where `I_(1)` current lower wire, `d` separation between wires.
Force on any small portion of upper wire having length `dl` is `dF=(mu_(0)I_(1)I_(2)dl)/(2pid),` where `I_(2)` current in the upper wire. If directions of current in the wires is appropriate then upper wire can be in equilibrium if its weight is balanced by magnetic force. Now answer the following questions.
Equilibrium separation between the two wires is
View SolutionThere are two infinite parallel current carrying wires in vertical plane. Lower wire is fixed and upper wire is having a linear mass density `lambda`. Two wires are carrying currents `I_(1)` and `I_(2)`. Now upper wire is placed in a magnetic field produced by lower wire. Magnetic field due to lower wire at the location of upper wire is `(mu_(0)I)/(2pid)`, where `I_(1)` current lower wire, `d` separation between wires.
Force on any small portion of upper wire having length `dl` is `dF=(mu_(0)I_(1)I_(2)dl)/(2pid),` where `I_(2)` current in the upper wire. If directions of current in the wires is appropriate then upper wire can be in equilibrium if its weight is balanced by magnetic force. Now answer the following questions.
The upper wire can be in equilibrium if
View SolutionThere are two infinite parallel current carrying wires in vertical plane. Lower wire is fixed and upper wire is having a linear mass density `lambda`. Two wires are carrying currents `I_(1)` and `I_(2)`. Now upper wire is placed in a magnetic field produced by lower wire. Magnetic field due to lower wire at the location of upper wire is `(mu_(0)I)/(2pid)`, where `I_(1)` current lower wire, `d` separation between wires.
Force on any small portion of upper wire having length `dl` is `dF=(mu_(0)I_(1)I_(2)dl)/(2pid),` where `I_(2)` current in the upper wire. If directions of current in the wires is appropriate then upper wire can be in equilibrium if its weight is balanced by magnetic force. Now answer the following questions.
If upper wire is slightly displaced from its mean position and released it will perform simple harmonic motion. As wire then total mechanical energy of wire
View SolutionA closed current-carrying loop having a current I is having area A. Magnetic moment of this loop is defined as `vec(mu) = vec(IA)` where direction of area vector is towards the observer if current is flowing in anticlockwise direction with respect to the observer. If this loop is placed in a uniform magnetic field `vec(B)`, then torque acting on the loop is given by `vec(tau) = vec(mu) xx vec(B)`. Now answer the following questions:
A uniformly charged insulating ring is rotated in a uniform magnetic field about its own axis, then
View SolutionA closed current-carrying loop having a current I is having area A. Magnetic moment of this loop is defined as `vec(mu) = vec(IA)` where direction of area vector is towards the observer if current is flowing in anticlockwise direction with respect to the observer. If this loop is placed in a uniform magnetic field `vec(B)`, then torque acting on the loop is given by `vec(tau) = vec(mu) xx vec(B)`. Now answer the following questions:
Consider the situation shown in Fig., ring is having a uniformly distributed positive charge. Magnetic field is perpendicular to the axis of ring. Now ring is rotated in anticlockwise direction as seen from left hand side direction of magnetic torque acting on the ring is
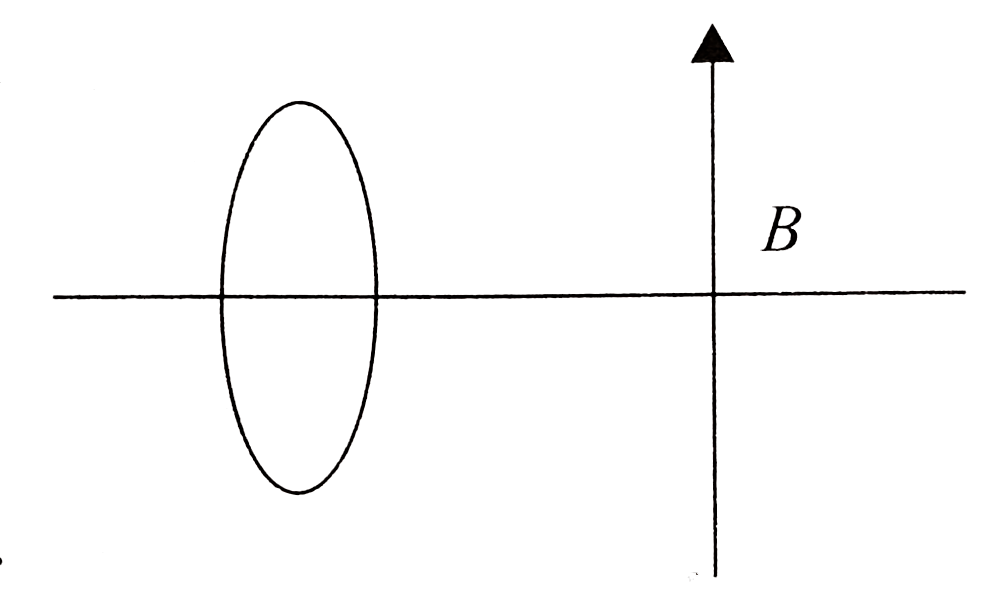
View SolutionA closed current-carrying loop having a current I is having area A. Magnetic moment of this loop is defined as `vec(mu) = vec(IA)` where direction of area vector is towards the observer if current is flowing in anticlockwise direction with respect to the observer. If this loop is placed in a uniform magnetic field `vec(B)`, then torque acting on the loop is given by `vec(tau) = vec(mu) xx vec(B)`. Now answer the following questions:
Let ring in the above question is having a radius R and a charge Q is uniformly distributed over it. Ring is rotated with a constant angular velocity `(omega)` as mentioned above.
Torque acting on the ring due to magnetic force is
View SolutionA wire frame in the form of a part of circle ( sector ) of radius 1 and resistance `R` is free to rotate about on axis passing through `O` and perpendicular to plane of paper as shown in the figure. The angle of the sector is `(pi)/(4)` and it is rotating with constant angular velocity `omega` as shown. Above line `PQ` uniform magnetic field of magnitude `B` exists in the direction perpendicular to plane of paper. In region `I` field is outward while in region `II`, field is inward.

Based on above information, answer the following questions `:`
The thermal energy dissipated in wire frame when it moves from region `I` to region `II`, is
View SolutionA wire frame in the form of a part of circle ( sector ) of radius 1 and resistance `R` is free to rotate about on axis passing through `O` and perpendicular to plane of paper as shown in the figure. The angle of the sector is `(pi)/(4)` and it is rotating with constant angular velocity `omega` as shown. Above line `PQ` uniform magnetic field of magnitude `B` exists in the direction perpendicular to plane of paper. In region `I` field is outward while in region `II`, field is inward.

Based on above information, answer the following questions `:`
Total thermal energy dissipated in one cycle is
View SolutionA wire frame in the form of a part of circle ( sector ) of radius 1 and resistance `R` is free to rotate about on axis passing through `O` and perpendicular to plane of paper as shown in the figure. The angle of the sector is `(pi)/(4)` and it is rotating with constant angular velocity `omega` as shown. Above line `PQ` uniform magnetic field of magnitude `B` exists in the direction perpendicular to plane of paper. In region `I` field is outward while in region `II`, field is inward.

Based on above information, answer the following questions `:`
Average power produced in wire framce is
View SolutionA rod has a total charge Q uniformly distributed along its length L. If the rod rotates with angular velocity `omega` about its end, compute its magnetic moment.

View SolutionAn infinitely long wire of uniform cross section carries a current whose current density varies as `j=br^(alpha)`. Where `b=(10^(7))/(pi)`unit,` alpha=.1`unit and `r` the distance from axis. The magnetic induction at a distance `0.25` from axis is given by `(nxx5)/(3)x10^(-2)` tesla. Find `n`
View SolutionA straight conductor of length `60cm` and mass `10gm` is suspended horizontally by a pair of flexible leads in a magnetic field of `0.4T` as shown in figure. A current at `0.41A` should be passed through the conductor to just remove the tension in the supporting cable. The total tension in the leads if the direction of current is reversed is found `1.96xx10^(-y)N`. Find `y` ?

View SolutionA thin wire is bent in the form of a semi circular ring of radius `R=0.9m` carries a current `I=1amp` . The magnetic induction at a point `P` as shown in the fig. is given by `nX10^(-7)` Tesla. Find the value of `n.[ln(sqrt(2)+1)=0.9]`

View SolutionA particle having a charge `q=1C` and mass `m=0.5kg` is projected on a rough horizontal plane `(x,y)` from a point `(15m,0,0)` with a initial velocity `vec(v)=20j`. In space a uniform electric field `vec(E)=25(-hat(k))` and magnetic filed `vec(B)=10(-hat(k))`. The acceleration due to gravity `g=10sec^(-2)` and co`-` efficient of friction `mu=0.5` . The particle moves on a spiral path and reaches to the origin . The time taken by particle to reach origin is found `yxx10sec`. Find `y`.
View SolutionA long straight wire carries a current `I_(0)=100amp` , a particle having a positive charge `q=100C` and mass `m=10 g m s` is kept at a distance `x_(0)=10m` from the axis of the wire is projected away from it with a speed `v_(0)=10m//sec`. Find the maximum separation between particle and wire is found to be `yxx10m` Find `y`.
View SolutionA particle of mass m and charge + q is projected from origin with velocity `vec(V)=V_(0)hati` in a magnetic field `vec(B)=-(B_(0)x)hatk.` Here `V_(0)` and `B_(0)` are positive constants of proper dimensions. Find the radius of curvature of the path of the particle when it reaches maximum positive x co-ordinate.
View SolutionIf the work required to move the conductor shown in figure, one full turn in the positive direction at a rotational frequency `N` revolutions per minute, if `vec(B)=B_(0)hat(a)_(r)(B_(0)` is positive constant and `hat(a)_(r)` is a unit vector in radial direciton `) ,` is `y pi r B_(0)il`. Then `y` is .

View SolutionA long straight metal rod has a very long hole of radius a drilled parallel to rod as shown in the figure. If the rod carries a current `i`. Find the magnetic field `(a)` on the axis of the rod. `(b)` on the axis of the hole.

View SolutionThere exists a uniform and constant magnetic field of strength `B` in the space betweent he plates of a charged parallel plate capacitor. The charge density on the plate is `sigma` and length of the plate is `l`. An electron is projected in the space between the plates along the length of the plate. It is foudn that velcoity of the electron does not change. Find the time taken by the electron to come out of the capacitor. The figure describes the situtation. Ignore the gravity.

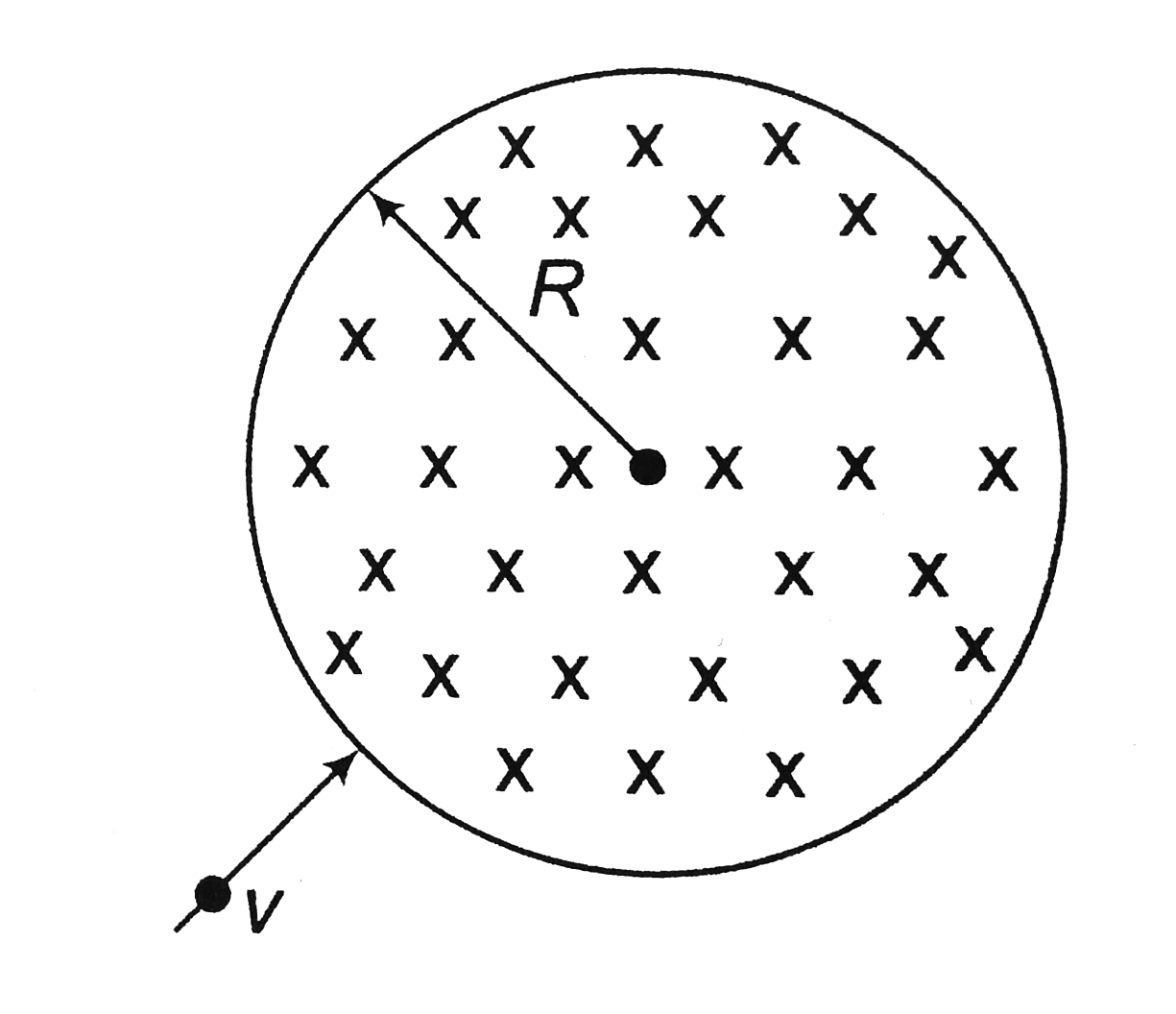
View SolutionA particle of mass `m` having a charge q enters into a circular region of radius `R` with velocity `v` directed towards the centre. The strength of magnetic field is `B`. Find the deviation in the path of the particle.
View SolutionA loop, carring a current i, lying in the plane of the paper, is in the field of a long straight wire with current `i_0` (inward) as shown in Fig. Find the torque acting on the loop.

View SolutionA rectangular loop PQRS made from a uniform wire has length a, width b and mass m. It is free to rotate about the arm PQ, which remains hinged along a horizontal line taken as the y-axis (see figure). Take the vertically upward direction as the z-axis. A uniform magnetic field `vec(B) = (3 hat(i) + 4 hat(k)) B_(0)` exists in the region. The loop is held in the x-y plane and a current I is passed through it. The loop is now released and is found to stay in the horizontal position in equilibrium

(a) What is the direction of the current I in PQ?
(b) Find the magnetic force on the arm RS.
(c) Find the expression for I in terms of `B_(0)`, a, b and m
View SolutionA insulated square frame `ABCD` of side a is able to rotate about one of its side taken as positive `z`-axis. A magnetic field `B` is present in the region given by `vecB=B_(0)hatj`. A small block of mass `m` and charge `q` movable along side `CB` is initially near `C`, when frame lies in `x-z` plane. Now, frame is rotated by constant angular velocity `omega` about `z`-axis. Whole system lies in gravity free space. If after time `t` block reaches point `B`, find `B_(0)` in terms of `t`.

View SolutionA bar of mass `m` slides on a smooth horizontal conducting rail. A constant current `I` is maintained in the rod using a constant current generator as shown. There is a long straight conductor carrying current `I_(0)` parallel to the rod. Find the speed of the bar after it has travelled a distance `D`

View SolutionAn infinte wire place along z-axis has current `I_(1)` in positive z-direction A conducting rod placed in xy plane parallel to y-axis has current `I_(2)` in positive y-direction The ends of the rod subtend `+30^(@)` and `-60^(@)` at the origin with positive x direction The rod is at a distance a from the origin. Find net force on the rod .
View SolutionA charged particle carrying charge `q=10 muC` moves with velocity `v_1=10^6 ,s^-1` at angle `45^@` with x-axis in the xy plane and experience a force `F_1=5sqrt2 mN` along the negative z-axis. When the same particle moves with velocity `v_2=10^6 ms^-1` along the z-axis, it experiences a force `F_2` in y-direction.
Find the magnitude of the force `F_2`.
View SolutionDeuterons in a cyclotron describes a circle of radius `32.0cm`. Just before emerging from the `D's`. The frequency of the applied alternating voltage is `10MHz`. Find, `(a)` the magnetic flux density `( i.e.,` the magnetic field `), (b)` the energy and speed of the deuterons upon emergence.
View SolutionA ring of radius R having unifromly distributed charge Q is mounted on a rod suspended by two identical strings. The tension in strings in equilibrium is `T_0.` Now a vertical magnetic field is switched on and ring is rotated at constant angular velocity `omega`. Find the maximum `omega` with which the ring can be rotated if the strings can withstand a maximum tension of `3T_0 //2.`

View SolutionThe region between ` x=o and x = L` is filled with uniform, steady magnetic field `B_(0) hat(k)`. A particle of mass `m` , positive charge `q` and velocity `v_(0) hat(i)` travels along ` x-axis` and enters the region of the magnetic field. Neglect gravity throughout the question .
(a) Find the value of `L` if the particle emerges from the region of magnetic field with its final velocity at angle `30^(@)` to its initial velocity.
(b) Find the velocity of the particle and the time spent by it in the magnetic field, if the magnetic field now extends upto `2.1L`.
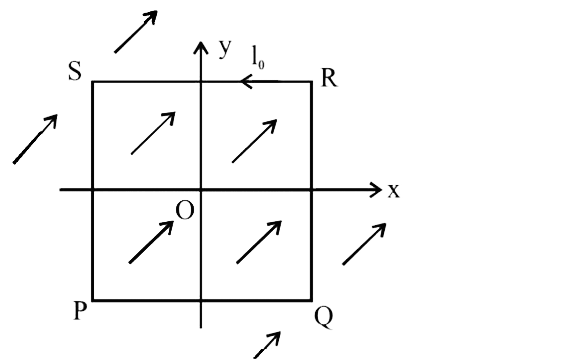
View SolutionA uniform constant magnetic field `B` is directed at an angle of `45^(@)` to the `x axis` in the ` xy`- plane . ` PQRS` is a rigid, square wire frame carrying a steady current `I_(0)`, with its centre at the origin `O`. At time ` t = 0`, the frame is at rest in the position as shown in figure , with its sides parallel to the ` x and y` axis. Each side of the frame is of mass `M` and length `L`.
(a) What is the torque `tau` about `O` acting on the frame due to the magnetic field?
(b) Find the angle by which the frame rotates under the action of this torque in a short interval of time `Deltat`, and the axis about this rotation occurs .`( Deltat is so short that any variation in the torque during this interval may be neglected .) Given : the moment of interia of the frame about an axis through its centre perpendicular to its about an axis through its centre perpendicular to its plane is `(4)/(3) ML^(2)`.
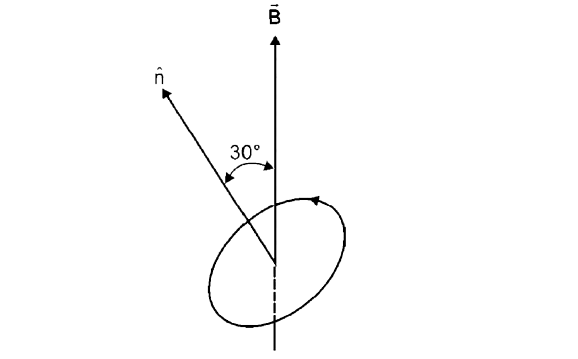
View SolutionAn electron in the ground state of hydrogen atom is revolving in anticlock-wise direction in a circular orbit of radius `R`.
(i) Obtain an experssion for the orbital magnetic dipole moment of the electron.
(ii) The atom is placed in a uniform magnetic induction `vec(B)` such that the plane - normal of the electron - orbit makes an angle of ` 30^(@)` with the magnetic induction . Find the torque experienced by the orbiting electron.
View Solution
LEVEL-V (SINGLE ANSWER QUESTION) questions and complete solutions for chapter MOVING CHARGES AND MAGNETISM of NARAYANA PHYSICS (HINGLISH) of Class 12
All Exercises from NARAYANA Class 12 PHYSICS MOVING CHARGES AND MAGNETISM
- C.U.Q (AMPERE.S CIRCUITAL LAW MAGNETIC FIELD DUE TO STRAIGHT CONDUCTOR )
- C.U.Q (CONVERSION OF MCG INTO AMMETER)
- C.U.Q (CONVERSION OF MCG INTO VOLTMETER)
- C.U.Q (CURRENT LOOP AND MAGNETIC DIPOLE)
- C.U.Q (FORCE BETWEEN TWO PARALLEL CURRENT CARRYING CONDUCTORS)
- C.U.Q (FORCE ON A MOVING CHARGE IN MAGNETIC FIELD)
- C.U.Q (FORCE ON A CURRENT CARRYING CONDUCTOR IN A MAGNETIC FIELD)
- C.U.Q (MOVING COIL GALVANOMETER)
- C.U.Q (TANGENT GALVANOMETER)
- C.U.Q (TORQUE ON CURRENT LOOP)
- C.U.Q-KEY
- EXERCISE - 1(C.W) (AMPERE.S CIRCUITAL LAW BIOT-SAVART LAW AND ITS APPLICATIONS)
- EXERCISE - 1(C.W) (CONVERSION OF MCG INTO AMMETER AND VOLTMETER)
- EXERCISE - 1(C.W) (CURRENT LOOP AND MAGNETIC DIPOLE)
- EXERCISE - 1(C.W) (CYCLOTRON)
- EXERCISE - 1(C.W) (FORCE ACTING A MOVING CHARGE IN MAGNETIC FIELD)
- EXERCISE - 1(C.W) (FORCE BETWEEN TWO PARALLEL CURRENT CARRYING CONDUCTORS)
- EXERCISE - 1(C.W) (FORCE ON A CURRENT CARRYING CONDUCTOR IN A MAGNETIC FIELD)
- EXERCISE - 1(C.W) (MOVING COIL GALVANOMETER)
- EXERCISE - 1(C.W) (SOLENOID AND TOROID)
- EXERCISE - 1(C.W) (TANGENT GALVANOMETER)
- EXERCISE - 1(C.W) (TORQUE ON CURRENT LOOP)
- EXERCISE - 1(H.W) (AMPERE.S CIRCUITAL LAW BIOT-SAVART LAW AND ITS APPLICATIONS
- EXERCISE - 1(H.W) (CONVERSION OF MCG INTO AMMETER AND VOLTMETER)
- EXERCISE - 1(H.W) (CYCLOTRON)
- EXERCISE - 1(H.W) (FORCE ACTING ON A MOVING CHARGE IN MAGNETIC FIELD)
- EXERCISE - 1(H.W) (FORCE BETWEEN TWO PARALLEL CURRENT CARRYING CONDUCTORS)
- EXERCISE - 1(H.W) (FORCE ON CURRENT CARRYING CONDUCTOR IN A MAGNETIC FIELD)
- EXERCISE - 1(H.W) (MOVING COIL GALVANOMETER)
- EXERCISE - 1(H.W) (SOLENOID AND TOROID)
- EXERCISE - 1(H.W) (TORQUE ON CURRENT LOOP)
- EXERCISE - 2(C.W) (AMPERE.S CIRCUITAL LAW BIO-SAVART LAW AND ITS APPLICATIONS)
- EXERCISE - 2(C.W) (CONVERSION OF MCG INTO AMMETER AND VOLTMETER)
- EXERCISE - 2(C.W) (CURRENT LOOP AND MAGNETIC DIPOLE)
- EXERCISE - 2(C.W) (FORCE ACTING ON A MOVING CHARGE IN MAGNETIC FIELD)
- EXERCISE - 2(C.W) (FORCE BETWEEN TWO PARALLEL CURRENT CARRYING CONDUCTORS)
- EXERCISE - 2(C.W) (MOVING COIL GALVANOMETER)
- EXERCISE - 2(C.W) (SOLENOID AND TOROID)
- EXERCISE - 2(C.W) (TANGENT GALVANOMETER)
- EXERCISE - 2(C.W) (TORQUE ON CURRENT LOOP)
- EXERCISE - 2(H.W) (AMPERE.S CIRCUITAL LAW BIO-SAVART LAW AND ITS APPLICATIONS)
- EXERCISE - 2(H.W) (CURRENT LOOP AND MAGNETIC DIPOLE)
- EXERCISE - 2(H.W) (FORCE ACTING A MOVING CHARGE IN MAGNETIC FIELD)
- EXERCISE - 2(H.W) (SOLENOID AND TOROID)
- EXERCISE - 2(H.W) (TANGENT GALVANOMETER)
- EXERCISE - 3
- EXERCISE - 4
- ILLUSTRATION
- Level -II (H.W)
- Level =I (H.W)
- LEVEL-I(C.W)
- Level-II(C.W)
- LEVEL-III
- LEVEL-V (SINGLE ANSWER QUESTION)
- LEVEL-VI (SINGLE ANSWER QUESTION)
- NCERT Based Questions
- W.E.