Complete Solutions to Linear Programming of chapter LINEAR PROGRAMMING of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | LINEAR PROGRAMMING |
| NCERT EXEMPLAR | Linear Programming |
| Number Of Questions | 45 |
| Academic Year | 2023-24 |
Determine the maximum value of Z=11x+7y subject to the constraints `2x+y le 6 , x le 2, x ge 0, y ge 0`
View SolutionMaximise Z=3x+4y, Subjected to the constraints `x+y le1, x ge 0, y ge 0`
View SolutionMaximise the function `Z=11x+7y`, subject to the constraints `x le 3, yle 2, x ge 0, y ge 0`
View SolutionMinimise Z=13x-15y subject to the constraints ` x+y le 7, 2x-3y+6 ge 0, x ge 0, x ge 0, and y ge 0`
View SolutionDetermine the maximum value of Z=3x+4y, if the feasible reigon (shaded) for a LPP is shown in following figure
View SolutionFeasible region (shaded) for a LPP is shown in following figure. Maximise Z=5x+7y.

View SolutionThe feasible region for an LPP is shown in following figure. Find the minimum value of `Z=11x+7y.`

View SolutionRefer to question 7 above. Find the maximum value of Z.
View SolutionThe feasible region for a LPP is shown in the following figure. Evaluate Z=4x+y at each of the corner points of the region. Find the minimum value of Z, if it exists

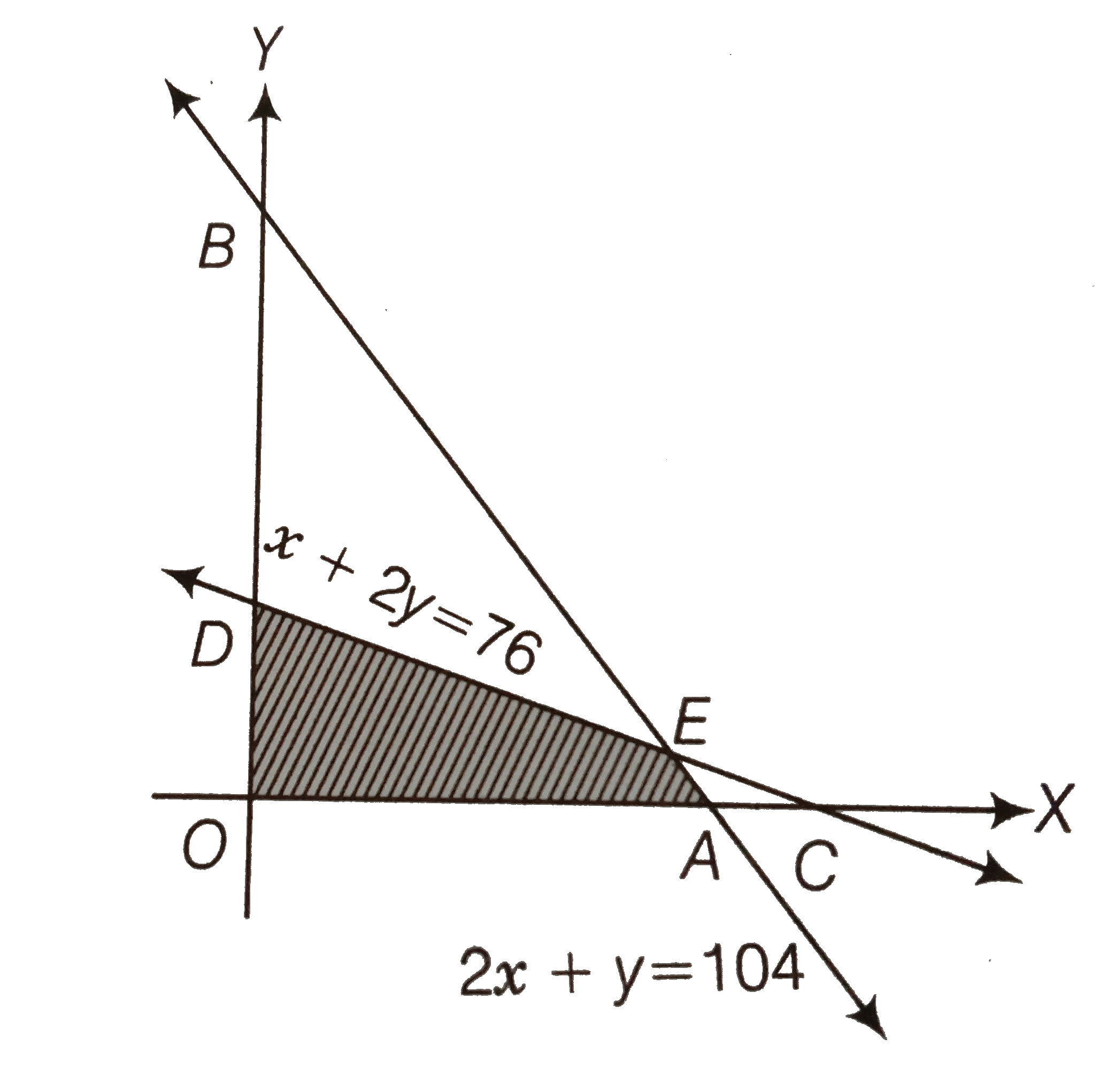
View SolutionIn the following the feasible region (shaded) for a LPP is shown Determine the maximum and minimum value of `Z=x+2y`
View SolutionIn the manufacturer of electronic circuits has a stock of 200 resistors, 120 transistors and 150 capacitors and is required to produce two types of circuits A and B. Type A requires 20 resistors, 10 transistors and 10 capacitors. Type B requires 10 resistros, 20 transistors and 30 capacitors, If the profit on type A circuit is 50 and that on type B circuit is 60 formulate this problem as LPP, so that hte manufacturer can maximise his profit.
View SolutionA firm has to transport 1200 packages using large vans which can carry 200 packages each and small vans which can take 80 packages each. The cost for engaging each large van is 400 and each small van is 200. Not more than 3000 is to be spent on the job and the number of large vans cannot exceed the number of small vans. Formulate this problem, a LPP given that the objective is to minimise cost.
View SolutionA company manufactures two types of screws A and B. all the screws have to pass through a threading machine and a slotting machine. A box of type A screw requires 2min on the threading machine and 3 min on the slotting machine. A box of type B screw requires 8 min on the threading machine and 2 min on the slotting machine. In a week each machine is availbale for 60h. On selling these screws, the company gets a profit of 100 box on type A screw and 170 per box on type B screws. Formulate this problem as a LPP given that the objective is to maximise profit.
View SolutionA company manufacutres two types of sweaters type A and type B. It costs 360 to make type A sweater and 120 to make a type B sweater. The company can make atmost 300 sweater and spent atmost 72000 a day. The number of sweaters of type B cannot exceed the number of sweaters of type A by more than 100. The company makes a profit of 200 for each sweater of type A and 120 for every sweater of type B. Formulate this problem as a LPP to maximise the profit to the company.
View SolutionA man rides his motorcycle to the speed 50 km/h. He has to spend 2per km on petrol. If the rides it at a faster speed of 80km/h, the petrol cost increases to 3 per km. He wishes to find the maximum distnace that he can travel. Express this problem as a linear programming problem.
View SolutionRefers to question 11. How many of circuit of type A and of type B, should be produced by the manufacture, so as to maximise hi profit? Determine the profit.
View SolutionRefers to question 12. i.e Z represents cost , if `Z=400x+200y, x+2y ≥ 30`, `x-y=0` and `5x+2y ≥ 30`, What will be the minimum cost?
View SolutionRefers to question 13. Solve the liner progamming problem and deterimine profit to the manufacturer.
View SolutionRefers to question 14. How many sweaters of each type of should the company make in an day to get a maximum profit? What is the maximum profit?
View SolutionRefers to question 15. Determine the maximum distance that the man can travel.
View SolutionMaximise Z=x+y subject to `x+4y le 8 , 2x+3y le 12, 3x+y le 9, x ge 0, and y ge 0`
View SolutionA manufacture produces two models of bike model X and model Y. Model X takes a 6 man hours to make per unit, while model Y takes 10 man hours per unit. There is a total of 450 man hour availbale per week. Handling and marketing costs are 2000 and 1000 per unit of model X and Y, respectively. The tota funds available for these purposes are 8000 per week. Profits per unit for models X and Y are 1000 and manufacturer produce, so, as to yeild a maximum profit? Find the maximum profit.
View SolutionIn order to supplement daily diet, a person wishes to take some X an some wishes Y tablets. The constents of iron, calcium and vitamins in X and Y (in mg/tablet) are given as below

The person need atleast 18 mg of iron of calcium 16 mg of vitamines. The price of each talet of X and Y is 2 and 1, respectively. How many tablets of each should the person take in order to satisfy the above requirements at the minimum cost?
View SolutionA company makes 3 model of calculators, A, B and C at factory I and factory II. The company has orders for atleast 6400 calculators of model A, 4000 calculators of model 8 and 4800 calculators of model C. At factory I, 50 calculators of model A, 50 of model 8 and 30 of model C are made everyday, at factory II, 40 calculators of model A, 20 of model B and 40 of model C are made everyday. It costs ? 12000 and 1 15000 each day to operate factory I and II, respectively. Find the number of days each factory should operate to minimise the operating costs and still meet the demand.
View SolutionMinimise and minise `Z=3x-4y` subject to `x-2y le 0, -3x+y le 4, x-y le 6 and x,y le 0`
View SolutionThe corner points of the feasible region determined by the system of linear contraints are (0,0), (0,40),( 20,40),(60,20),(60,0). The objective function is Z=4x+3y. Compare the quantity in Column A and Column B.
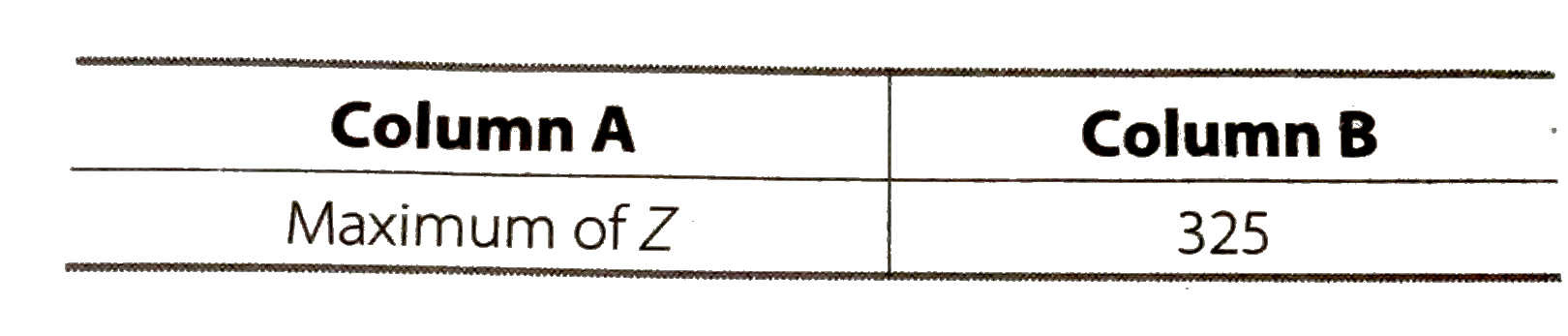
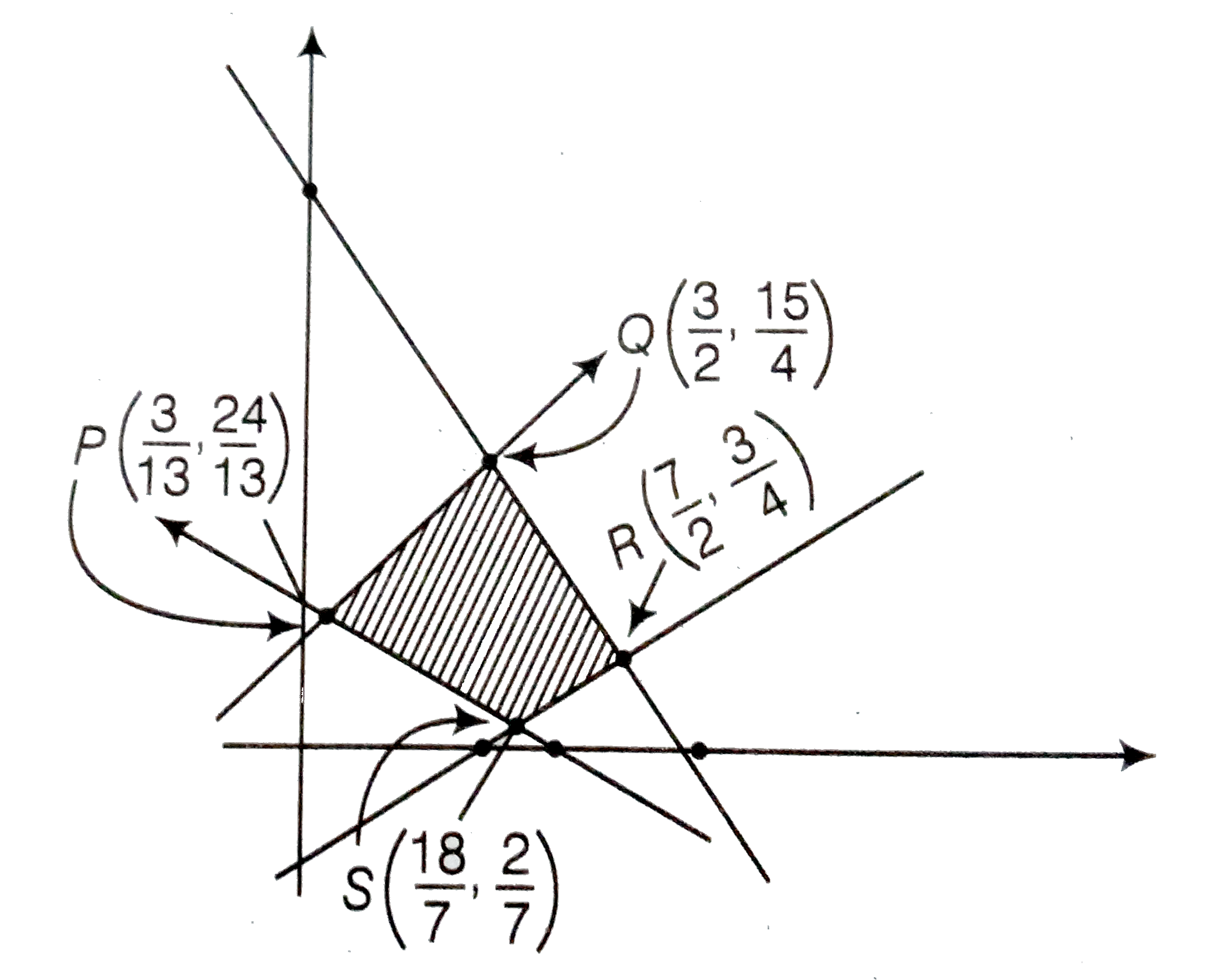
View SolutionThe feasible solution for a LPP is shown in following figure. Let `Z=3x-4y` be the objective function, Minimum of `Z` occurs at
View SolutionRefers to question 27. Maximum of Z occurs at
View SolutionRefers to question 7, maximum value of Z+minimum value of Z is equal to
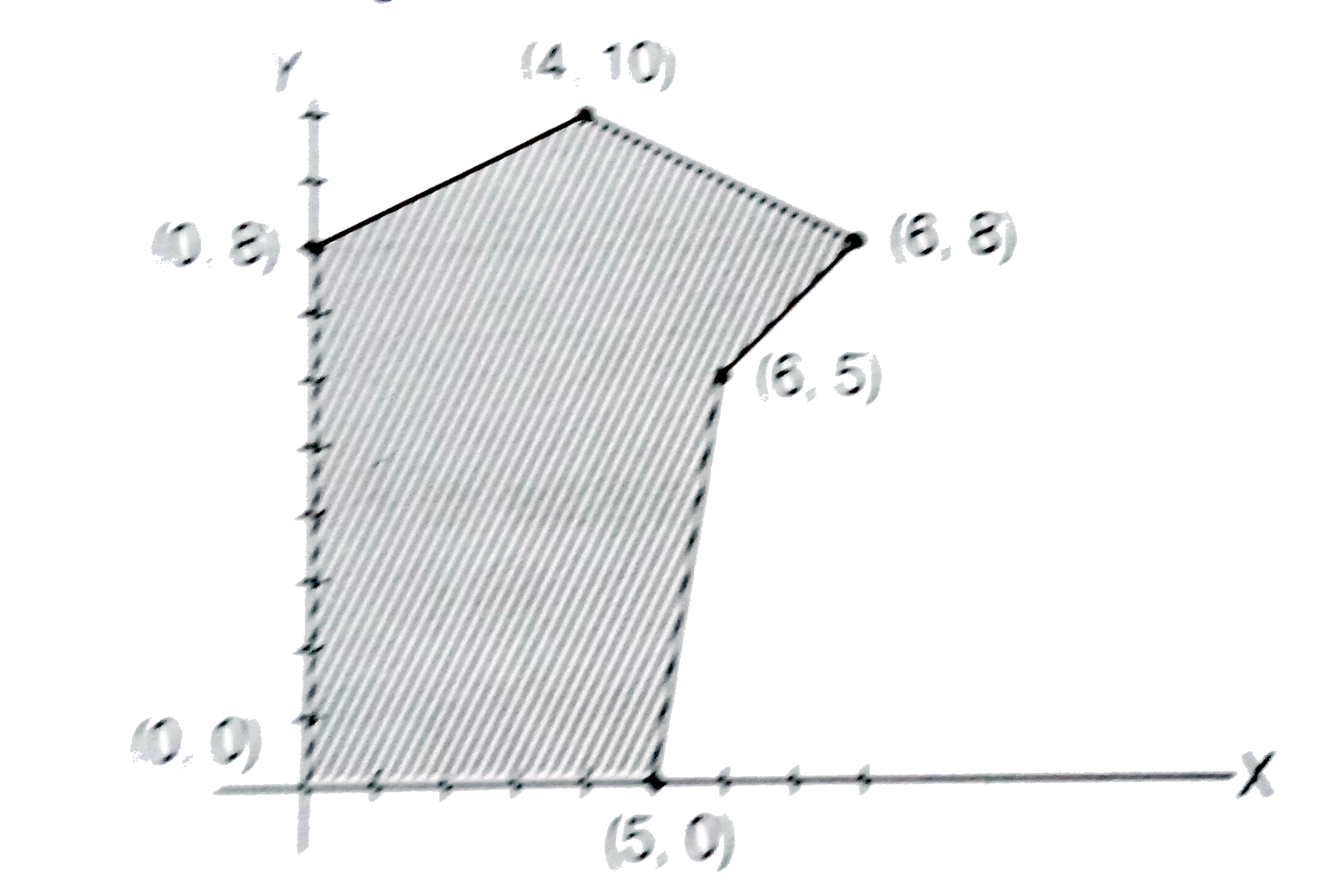
View SolutionThe feasible region for an `LPP` is shown in the following figure. Let `F=3x-4y` be the objective function. Maximum value of `F` is
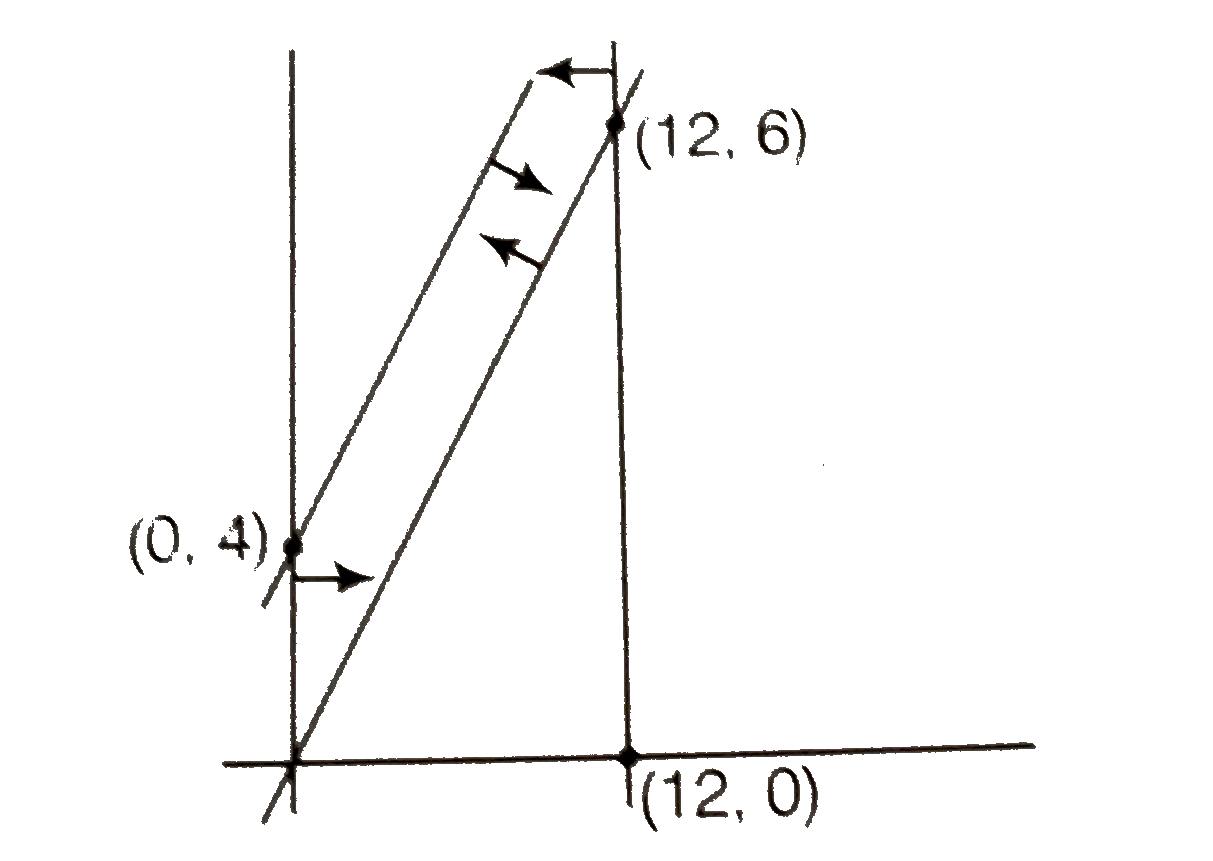
View SolutionRefers to question 30. Minimum value of F is
View SolutionCorner points of the feasible region for an LPP are `(0,2),(3,0),(6,0),(6,8)`, and `(0,5)`. Let `F = 4x+6y` be the objective function. Determine the minimum value of `F` occurs at
View SolutionRefers to question 32, maximum of F-minimum of F is equal to
View SolutionCorner points of the feasible region determined by the system of linear constraints are (0,3), (1,1), and (3,0). Let `Z=px+qy.` Where `p, q lt 0` Condition on p and q, so that the minimum of Z occurs at (3,0) and (1,1) is
View SolutionIn a LPP, the linear inequalities or restrictions on the variables called.
View SolutionIn a LPP, the objective function is always.
View SolutionIn the feasible region for a LPP is ..., then the optimal value of the objective function Z= ax + by may or may not exist.
View SolutionIn a LPP, if the objective function Z=ax+by has the same maximum value of two corner points of the feasible region, then every point of the line segment joining these two points give the same ..value.
View SolutionA feasible region of a system of linear inequalities is said to be ..., if it can be enclosed within a circle.
View SolutionA corner point of a feasible region is a point in the reqion which is the of two boundary lines.
View SolutionThe feasible region for an LPP is always a..polygon
View SolutionIf the feasibile region for a LPP is undoubed, maximum or minimum of the objective function Z = ax + by may or may not exist.
View SolutionMaximum value of the objective function Z = ax +by in a LPP always occurs at only one corner point of the feasible region.
View SolutionIn a LPP, the maximum value of the objective function Z = ax +by is always 0, if origin is one of the corner point of the feasible region.
View SolutionIn a LPP, the maximum value of the objective function Z = ax +by is always finite.
View Solution
Linear Programming questions and complete solutions for chapter LINEAR PROGRAMMING of NCERT MATHS (HINGLISH) of Class 12