Complete Solutions to PROBLEMS of chapter GRAVITATION of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | GRAVITATION |
| RESNICK AND HALLIDAY | PROBLEMS |
| Number Of Questions | 63 |
| Academic Year | 2023-24 |
A particle of mass `m_1 = 0.67 kg` is a distance d = 23 cm from one end of a uniform rod with length L = 2.5 m and mass M = 4.0 kg. What is the magnitude of the gravitational for `vecF` the particle from the rod ?

View SolutionTwo neutron stars are separated by a distance of `1.0 xx 10^11` m. They each have a mass of `1.0xx10^30` kg and a radius of `2.0 xx 10^5` m. They are initially at rest with respect to each other. As measured from that rest frame, how fast are they moving when (a) their separation has decreased to one-half its initial value and (b) they are about to collide ?
View SolutionIn a certain binary-star system, each star has the same mass as our Sun, and they revolve about their center of mass. The distance between them is the same as the distance between Earth and the Sun. What is their period of revolution in years ?
View SolutionMiniature black holes. Left over from the big-bang beginning of the uniberse, tiny black holes might still wander through the universe. If one with a mass of `5.0 xx 10^11 kg` (and a radius of only `5.0 xx 10^(-16)m`) reached Earth, at what distance from your head would its gravitational pull on you match that of Earth's?
View SolutionA rocket is to be shot radially outward from Earth's surface. Neglecting Earth's rotation, find the radial distance from Earth's center that the rocket reaches if it is launched with (a) 0.400 times the escape speed from Earth and (b) 0.400 times the kinetic energy that is required to escape Earth. (c) At launch, what is the least mechanical energy required for it to escape Earth ?
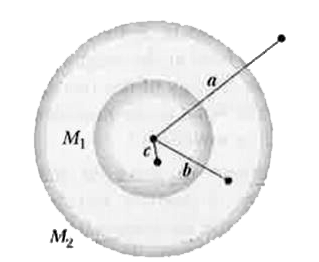
View SolutionTwo concentric sperical shells with uniformly distributed masses `M_1 = 5.00 xx 10^3 kg and M_2 = 9.00 xx 10^3 kg` are situated as shown. Find the magnitude of the net gravitational force on a particle of mass `m = 2.00` kg due to the shells, when the particle is located at radial distance (a) a = 11.0 m, (b) b = 6.00 m and (c) c = 2.00 m.
View SolutionAt what height above Earth's surface is the energy required to lift a satellite to that height equal to the kinetic energy required for the satellite to be in orbit at that height ?(b) For greater heights, which is greater, the energy for lifting or the kinetic energy for orbiting ?
View SolutionWe want to position a space probe along a line that extends directly toward the Sun in order to monitor solar flares. How far from Earth's center is the point on the line where the Sun's gravitational pull on the probe balances Earth's pull ?
View SolutionTwo satellites, A and B, both of mass `m = 150 kg`, move in the same circular orbit of radius `r = 7.87xx10^6`m around Earth but in opposite senses of rotationand therefore on a collision course. (a) Find the total mechanical energy `E_A + E_B` of the two satellites + Earth system before the collision. (b) If the collision is completely inelastic so that the wreckage remains as on piece of tangled meterial (mass = 2m), find the total mechanical energy immediately after the collision. (c) Just after the collision,is the wreckage falling directly toward Earth's center or orbiting around Earth ?
View SolutionA satellite is in a circular Earth orbit of radius r. The area A enclosed by the orbit depends on `r^2` because `A = pi r^2`. Determine how the following properties of the satellite depend on r. (a)period, (b) kinetic energy, (c ) angular momentum, and (d) speed.
View SolutionThree deminsions. Three point particles are fixed in place in a xyz coordinate system. Particle A, at the origin, has mass `m_A`. Particle B, at xyz coordinates (2.00d,1.00d. 200), has mass 2.00`m_A`, and particle C, at coordinates (-1.00d,2.00d,-3.00d), has mass `3.00m_A`. A fourth particle D,with mass `4.00 m_A`,is to be placed near the other particles. In terms of distance d, at what (a)x, (b)y, and (c)z coordinate should D be placed so that the net gravitational force on A from B, C, and D is zero ?
View SolutionA comet that was seen in April 574 by Chinese astronomers on a day known by them as the Woo Woo day was spotted again in May 1994. Assume the time between observations is the period of the Woo Woo day comet and its eccentricity is 0.9932. What are (a) the semimajor axis of the comet's orbit and (b) its greatest distance from the Sun in terms of the mean orbital radius `R_p` of Pluto?
View SolutionA uniform metal sphere of radius `R` and mass `m` is surrounded by a thin uniform spherical shell of same mass and radius `4R`. The centre of the shell `C` falls on the surface of the inner sphere. Find the gravitational fields at points `A` and `B`.

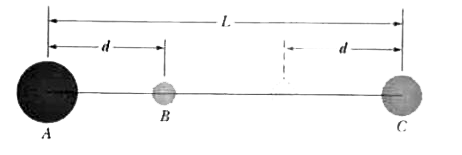
View SolutionThe three spheres in with masses `m_A = 80 g, m_B, = 10 g, and m,_C= 20 g`, have their centers on a common line, with L = 14 cm and d = 2.0 cm. You move sphere B along the line until its center-to-center separation from C is d = 2.0 cm. How much work is done on sphere B (a) by you and (b) by the net gravitational force on B due to spheres A and C?
View SolutionThe Sun and Earth each exert a gravitational force on the Moon. What is the ratio `F_("sun")//F_("Earth")` of these two forces? (The average Sun-Moon distance is equal to the Sun Earth distance.)
View SolutionThe first known collision between space debris and a functioning satellite occurred in 1996: At an altitude of 700 km, a year-old French spy satellite was hit by a piece of an Ariane rocket. A stabilizing boom on the satellite was demolished, and the satellite was sent spinning out of control. Just before the collision and in kilometers per hour, what was the speed of the rocket piece relative to the satellite if both were in circular orbits and the collision was (a) head-on and (b) along perpendicular paths?
View SolutionThe Sun's center is at one focus of Earth's orbit. How far from this focus is the other focus, (a) in meters and (b) in terms of the solar radius, `6.96 xx 10^8` m? The eccentricity is 0.0167, and the semimajor axis is `1.50 xx 10^11` m.
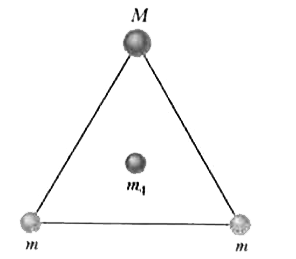
View SolutionAs seen in two spheres of mass m and a third sphere of mass M form an equilateral triangle, and a fourth sphere of mass `m_4` is at the center of the triangle. The net gravitational force on that central sphere from the three other spheres is zero. (a) What is M in terms of m? (b) If we double the value of `m_4` what then is the magnitude of the net gravitational force on the central sphere?
View SolutionA satellite is in circular orbit about Earth at an altitude of 300 km. What are its (a) orbital period, (b) orbital fre quency, and (c) linear speed?
View SolutionAn orbiting satellite stays over a certain spot on the equator of (rotating) Earth. What is the altitude of the orbit (called a geosynchronous orbit?
View SolutionWhat multiple of the energy needed to escape from Earth gives the energy needed to escape from (a) a moon of mass `1.472 xx 10^(23)` kg and radius `3.480 xx 10^6` m and (b) Jupiter?
View SolutionTwo particles are separated by 19 m when their gravitational attraction has a magnitude of `4.0 xx 10^(-12)` N. If the mass of particle 1 is 5.2 kg, what is the mass of particle 2?
View SolutionWhat is the minimum energy required to launch a satellite of mass m from the surface of a planet of mass M and radius R in a circular orbit at an altitude of 2R?
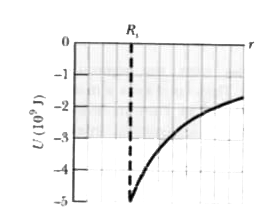
View SolutionGives the potential energy function U(r) of a projectile, plotted outward from the surface of a planet of radius `R_s`. If the projectile is launched radially outward from the surface with a mechanical energy of `-2.0 xx 10^9` J, what are (a) its kinetic energy at radius `r = 1.15R_s`, and (b) its turning point (see Section 8.4) in terms of `R_s`?
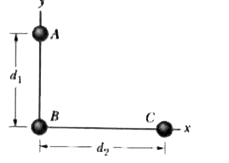
View SolutionThree 8.00 kg spheres are located at distances `d_1` = 0.300 m and `d_2` = 0.400 m. What are the (a) magnitude and (b) direction (relative to the positive direction of the x axis) of the net gravitational force on sphere B due to spheres A and C?
View SolutionA square of edge length 20.0 cm is formed by four spheres of masses `m_1 = 5.00 g, m_2 = 3.00 g, m_3 = 1.00 g, and m_4 = 5.00 g`. In unit-vector notation, what is the net gravitational force from them on a central sphere with mass `m_5 = 2.00 g`?

View SolutionIn deep space, sphere A of mass 20 kg is located at the origin of an x axis and sphere B of mass 10 kg is located on the axis at x = 0.95 m. Sphere B is released from rest while sphere A is held at the origin. (a) What is the gravitational potential energy of the two-sphere system just as B is released? (b) What is the kinetic energy of B when it has moved 0.15 m toward A?
View SolutionConsider an object of mass M that is small enough to be treated as a particle but large enough that a section of mass m can be removed and positioned 3.0 mm from the remaining part. To maximize the magnitude of the gravitational force between the removed section and the remaining part, what should the ratio of m/M be?
View SolutionA mars satellite moving in an orbit of radius `9.4xx10^3` km take 27540 s to complete one revolution. Calculate the mass of mars.
View SolutionIn 1610, Galileo used his telescope to discover four moons around Jupiter, with these mean orbital radii a and periods T.
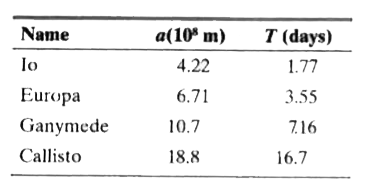
(a) Plot log a (y axis) against log T (x axis) and show that you get a straight line. (b) Measure the slope of the line and compare it with the value that you expect from Kepler's third law. (c) Find the mass of Jupiter from the intercept of this line with the y axis.
View SolutionThree identical stars of mass M form an equilateral triangle that rotates around the triangle's center as the stars move in a common circle about that center. The triangle has edge length L. What is the speed of the stars?
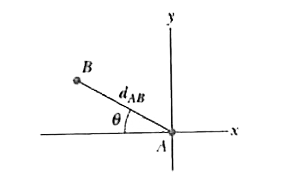
View SolutionThree point particles are fixed in position in an xy plane. Two of them, particle A of mass 6.00 g and particle B of mass 12.0 g, are shown with a separation of `d_(AB) = 0.500m`at angle `theta = 30^@`. Particle C, with mass 10.0 g, is not shown. The net gravitational force acting on particle A due to particles B and C is `2.77 xx 10^(-14)` N at an angle of `-163.8^@` from the positive direction of the x axis. What are (a) the x coordinate and (b) the y coordinate of particle C?
View SolutionA satellite, moving in an elliptical orbit, is 1440 km above Earth's surface at its farthest point and 180 km above at its closest point. Calculate (a) the semimajor axis and (b) the eccentricity of the orbit.
View SolutionHunting a black hole. Observations of the light from a certain star indicate that it is part of a binary (two-star) system. This visible star has orbital speed y = 270 km/s, orbital period T = 1.70 days, and approximate mass `m_1 = 6M_s` where `M_s` is the Sun's mass, `1.99 xx 10^30 kg`. Assume that the visible star and its companion star, which is dark and unseen, are both in circular orbits . What integer multiple of M gives the approximate mass `m_2` of the dark star?

View Solution(a) What is the escape speed on a spherical asteroid whose radius is 700 km and whose gravitational acceleration at the surface is `4.5 m//s^2`? (b) How far from the surface will a particle go if it leaves the asteroid's surface with a radial speed of 1000 m/s? (c) With what speed will an object hit the asteroid if it is dropped from 1000 km above the surface?
View SolutionAt what altitude above Earth's surface would the gravitational acceleration be `2.0 m//s^2`?
View SolutionAn asteroid, whose mass is `2.0 xx 10^(-4)` times the mass of Earth, revolves in a circular orbit around the Sun at a distance that is 3.0 times Earth's distance from the Sun. (a) Calculate the period of revolution of the asteroid in years. (b) What is the ratio of the kinetic energy of the asteroid to the kinetic energy of Earth?
View SolutionThe radius `R_h` and mass`M_h` of a block hole are related by `R_h = 2GM_h//c^2`, where c is the speed of light. Assume that the gravitational acceleration `a_g` of an object at a distance `r_o = 1.001R_h` from the center of a block hole is given by (it is, for large block holes). (a) In terms of `M_h` increases ? (b) Does `a_g" at "r_o` increase or decease as `M_h`increases ? (b) Does `a_g" at " r_o` increase or decrease as `M_h` increase ? (c) What is `a_g" at "r_o` for a very large black hole whose mass is `1.55 xx 10^12` times the solar mass of `1.99 xx 10^30` kg ? (d) If an astronaut of height 1.66 m is at `r_o` with her feet down, what is the difference in gravitational acceleration between her head the difference in gravitaional acceleration between her head and feet ? (e) Is the tendency to stretch the astronaut severe ?
View SolutionOne way to attack a satellite in Earth orbit is to launch a swarm of pellets in the same orbit as the satellite but in the opposite direction. Suppose a satellite in a circular orbit 500 km above Earth's surface collides with a pellet having mass 5.0 g. (a) What is the kinetic energy of the pellet in the reference frame of the satellite just before the collision? (b) What is the ratio of this kinetic energy to the kinetic energy of a 5.0 g bullet from a modern army rifle with a muzzle speed of 950 m/s?
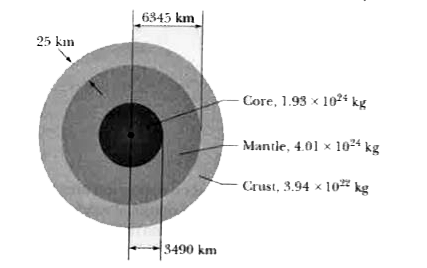
View SolutionNot to scale, a cross section through the interior of Earth. Rather than being uniform throughout, Earth is divided into three zones: an outer crust, a mantle, and an inner core. The dimensions of these zones and the masses contained within them are shown on the figure. Earth has a total mass of `5.98 xx 10^21` kg and a radius of 6370 km. Ignore rotation and assume that Earth is spherical. (a) Calculate a at the surface. (b) Suppose that a bore hole (the Mohole) is driven to the crust-mantle interface at a depth of 25.0 km, what would be the value of `a_g` at the bottom of the hole? (C) Suppose that Earth were a uniform sphere with the same total mass and size. What would be the value of `a_g` at a depth of 25.0 km? (Precise measurements of `a_g` are sensitive probes of the interior structure of Earth, although results can be clouded by local variations in mass distribution.)
View SolutionMoon effect. Some people believe that the Moon controls their activities. If the Moon moves from being directly on the opposite side of Earth from you to being directly overhead, by what percent does (a) the Moon's gravitational pull on you increase and (b) your weight (as measured on a scale) decrease? Assume that the Earth-Moon (center-to-center) distance is `3.82 xx 10^8` m and Earth's radius is `6.37 xx 10^6` m.
View SolutionIn Problem 29, what ratio m/M gives the least gravitational potential energy for the system?
View SolutionA solid sphere has a uniformly distributed mass of `1.0 xx 10^4 g` and a radius of 1.0 m. What is the magnitude of the gravitational force due to the sphere on a particle of mass m = 2.0 kg when the particle is located at a distance of (a) 1.5 m and (b) 0.50 m from the center of the sphere? (c) Write a general expression for the magnitude of the gravitational force on the particle at a distance `r le 1.0` , from the center of the sphere.
View SolutionTwo Earth satellites, A and B, each of mass m, are to be launched into circular orbits about Earth's center. Satellite A is to orbit at an altitude of 6370 km. Satellite B is to orbit at an altitude of 19 850 km. The radius of Earth R, is 6370 km. (a) What is the ratio of the potential energy of satellite B tu trial of satellite A, in orbit? (b) What is the ratio of the kinetic energy of satellite R to that of satellite A, in orbit? (C) Which satellite has the greater total energy if each has a mass of 14.6 kg? (d) By how much?
View SolutionFour particles, each of mass 20.0 g, that form a square with an edge length of d = 0.600 m. If d is increased to 1.20 m, what is the change in the gravitational potential energy of the four-particle system?
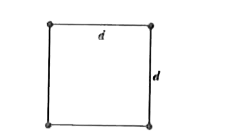
View SolutionTwo dimensions. Three point particles are fixed in place in an xy plane. Particle A has mass `m_A`, particle B has mass `2.00m_A` and particle C has mass `3.00m_A`. A fourth particle D, with mass `12.0m_A` is to be placed near the other three particles. In order for the net force on particle A due to the other three particles to be zero, where should particle D be located? Give (a) the distance from A in terms of d and (b) the angle relative to the positive direction of the x axis?
View SolutionWhat are (a) the speed and (b) the period of a 400 kg satellite in an approximately circular orbit 900 km above the surface of Earth? Suppose the satellite loses mechanical energy at the average rate of `1.4 xx 10^5` J per orbital revolution. Adopting the reasonable approximation that the satellite's orbit becomes a "circle of slowly diminishing radius," determine the satellite's (c) altitude, (d) speed, and (e) period at the end of its 1500th revolution. (f) What is the magnitude of the average retarding force on the satellite? Is angular momentum around Earth's center conserved for (g) the satellite and (h) the satellite-Earth system (assuming that system is isolated)?
View SolutionZero, a hypothetical planet, has a mass of `5.0 xx 10^2` kg, a radius of `3.5 xx 10^6` m, and no atmosphere. A 10 kg space probe is to be launched vertically from its surface. (a) If the probe is launched with an initial energy of `5.0 xx 10^7` J, what will be its kinetic energy when it is `4.0 xx 10^6`m from the center of Zero? (b) If the probe is to achieve a maximum distance of `8.0 xx 10^6` m from the center of Zero, with what initial kinetic energy must it be launched from the surface of Zero?
View SolutionTwo small spaceships, each with mass m = 1500 kg, are in the circular Earth orbit of at an altitude h of 400 km. Igor, the commander of one of the ships, arrives at any fixed point in the orbit 90 s ahead of Picard, the commander of the other ship. What are the (a) period `T_0` and (b) speed `v_0` of the ships? At point P in Fig. 13-35, Picard fires an instantaneous burst in the forward direction, reducing his ship's speed by 100%. After this burst, he follows the elliptical orbit shown dashed in the figure. What are the (c) kinetic energy and (d) potential energy of his ship immediately after the burst? In Picard's new elliptical orbit, what are (e) the total energy E. (f) the semimajor axis a, and (g) the orbital period T? (h) How much earlier than Igor will Picard return to P?
View SolutionThe mean distance of Mars from the Sun is 1.52 times that of Earth from the Sun. From Kepler's law of periods, calculate the number of years required for Mars to make one revolution around the Sun, compare your answer with the value given in Appendix C.
View Solution(a) What will an object weigh on the Earth's surface if it weighs 160 N on the Moon's surface? (b) How many Earth radii must this same object be from the center of Earth if it is to weigh the same as it does on the Moon?
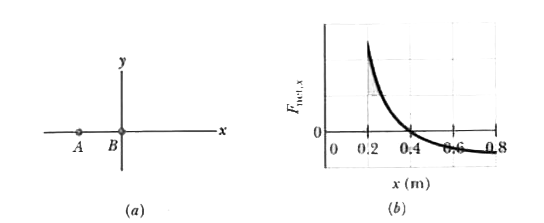
View SolutionParticle A is fixed in place at x = -0.20 m on the x axis and particle B, with a mass of 1.5 kg, is fixed in place at the origin. Particle C (not shown) can be moved along the x axis, between particle B and `x = oo`. shows the x component `F_("net,x")` of the net gravitational force on particle B due to particles A and C, as a function of position x of particle C. The plot actually extends to the right, approaching an asymptote of `-4.17 xx 10^(-10)` N as `x to oo`. What are the masses of (a) particle A and (b) particle C?
View SolutionA uniform solid sphere of radius R produces a gravitational acceleration of `a_g` on its surface. At what distance from the sphere's center are there points (a) inside and (b) outside the sphere where the gravitational acceleration is `a_g`/2?
View SolutionA satellite is put in a circular orbit about Earth with a radius equal to two-thirds the radius of the Moon's orbit. What is its period of revolution in lunar months? (A lunar month is the period of revolution of the Moon)
View SolutionThe mean diameters of Mars and Earth are `6.9 xx 10^3` km and `1.3 xx 10^4` km, respectively. The mass of Mars is 0.11 times Earth's mass. (a) What is the ratio of the mean density (mass per unit volume) of Mars to that of Earth? (b) What is the value of the gravitational acceleration on Mars? (c) What is the escape speed on Mars?
View SolutionA spherical hollow inside a lead sphere of radius R = 2.00 cm, the surface of the hollow passes through the center of the sphere and "touches" the right side of the sphere. The mass of the sphere before hollowing was M = 2.95 kg. With what gravitational force does the hollowed-out lead sphere attract a small sphere of mass m = 0.950 kg that lies at a distance d 9.00 cm from the center of the lead sphere, on the straight line connecting the centers of the spheres and of the hollow?

View SolutionAt what angular speed of rotation is the surface material on the equator of a neutron star on the verge of flying off the star if the star is spherical with a radius of 18.0 km and a mass of `7.72 xx 10^24` kg?
View SolutionMountain pull. A large mountain can slightly affect the direction of "down" as determined by a plumb line. Assume that we can model a mountain as a sphere of radius R = 1.80 km and density (mass per unit volume) `2.6 x 10^3 kg//m^3`. Assume also that we hang a 0.50 m plumb line at a distance of 3R from the sphere's center and such that the sphere pulls horizontally on the lower end. How far would the lower end move toward the sphere?
View SolutionThe Sun, which is `2.2 xx 10^20` m from the center of the Milky Way galaxy, revolves around that center once every `2.5 xx 10^8` years. Assuming each star in the Galaxy has a mass equal to the Sun's mass of `2.0 xx 10^30` kg, the stars are distributed uniformly in a sphere about the galactic center, and the Sun is at the edge of that sphere, estimate the number of stars in the Galaxy.
View SolutionAssume a planet is a uniform sphere of radius R that (somehow) has a narrow radial tunnel through its center (Fig. 13-8). Also assume we can position an apple anywhere along the tunnel or outside the sphere. Let `F_R` be the magnitude of the gravitational force on the apple when it is located at the planet's surface. How far from the surface is there a point where the magnitude is `1//3F_R` if we move the apple (a) away from the planet and (b) into the tunnel?
View Solution(a) What is the gravitational potential energy of the two-particle system in Problem 22? If you triple the separation between the particles, how much work is done (b) by the gravitational force between the particles and (c) by you?
View SolutionA satellite circles a planet of unknown mass in circular orbit of radius `2xx10^(7)m`. The magnitude of the gravitational forcce exerted on the satellite by the planet is 80 N . The kinetic energy of satellite in this orbit in joule is
View SolutionA 30 kg satellite has a circular orbit with a period of 2.0 h and a radius of `9.0 xx 10^6` m around a planet of unknown mass. If the magnitude of the gravitational acceleration on the surface of the planet is `6.0 m//s_2`. what is the radius of the planet?
View Solution
PROBLEMS questions and complete solutions for chapter GRAVITATION of RESNICK AND HALLIDAY PHYSICS (HINGLISH) of Class 12