Complete Solutions to SAMPLE PROBLEM of chapter WAVES-I of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | WAVES-I |
| RESNICK AND HALLIDAY | SAMPLE PROBLEM |
| Number Of Questions | 11 |
| Academic Year | 2023-24 |
A transverse wave traveling along an x axis has the form given by `y=y_(m) sin (kx pm omegat +phi)`.
Figure 16-10a gives the displacements of string elements as a function fo x, all at time t=0. Figure. 16-10b gives the displacements of the elements at x=0 as a function of t. Find the values of the quantities shown in Eq. 16-20. including the corret choice of sign.
View SolutionA wave traveling along a string is described by
y(x,t)=(0.00327 m) sin(72.1x - 2.721). (16-21) in which the numerical constants are in SI units (72.1 rad/m and 2.72 rad/s)
(a) What is the velocity of this wave?
(b) What is the displacement y at x= 22.5 cm and t=18.9s?
(c) What is the transverse velocity u of the string element at x =22.5 cm at time t= 18.9s? (This velocity, which is associated with the transverse oscillation of a string elenient, is parallel to the y axis. Do not confuse it with the constant velocity at which the wave form moves along the x axis.)
(d) What is the transverse acceleration of our string element at 18.9 3?
View SolutionIn Fig. 16-13, two strings have been tied together with a knot and then stretched between two rigid supports. The strings have linear densities `mu_(1) = 1.4 xx 10^(-4)" kg/m "and mu_(2)=2.8. xx 10^(-4)"kg/m".` Their lengths are `L_1= 3.0 m and L_2=2.0m,` and string 1 is under a tension of 400 N. Simultaneously, on each string a pulse is sent from the rigid support end, toward the knot. Which pulse reaches the knot first.
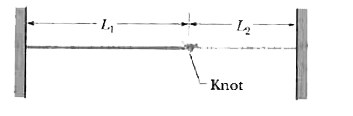
Figure 18-13 Two strings, of lengths `L_1 and L_2`, tied together with a knot and stretched between two rigid supports.
View SolutionA string has linear density `mu=525 g//m` and is under tension `tau=45N`. We send a sinusoidal wave with frequency f=120Hz and amplitude `y_(m)=8.5` mm along the string. At what average rate does the wave transport energy?
View SolutionTwo identical sinusoidal waves, moving in the same direction along a stretched string, interfere with each other. The amplitude y of each wave is 9.8 mm, and the phase difference p between them is `100^@.`
(a) What is the amplitude y. of the resultant wave due to the interference, and what is the type of this interference?
(b) What phase difference, in radians and wavelengths, will give the resultant wave an amplitude of 4.9 mm?
View SolutionTwo sinusoidal waves with the same amplitude of 4.0mm and the same wavelength traveled together along a string that is stretched along an x axis, the resultant wave due to their interference was recorded on video tape. The curves in Fig. 16-20 represent the resultant wave in two freeze frames, first as the solid curve and then, 1.0 ms later, as the dotted curve. The grid lines along the x axis are 1.0 cm apart, and the string clements oscillated vertically (perpendicular to the x axis) by 6.0 mm as the resultant wave passed through them. That wave moved a distance d =4.20 cm to the right in the 1.0 ms time interval. Write equations for the two interfering waves and for their resultant wave.
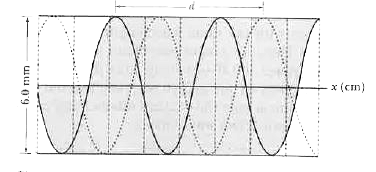
Figure 16-20 The resultant wave of two sinusoidal string wave traveling along an x axis is shown at two instants, between which the resultant wave travels distance d.
View SolutionA sinusidal wave with amplitude `y_(m)=0.5mm` and wavelength `lambda=0.4m.` is travelling on a string with speed v=12 m/s. At t=0 particle at x=0.1 m is located at y=0.25 mm and going down.
(a) Find equation of wave.
(b) Plot the sinusoidal wave at t=0.
View SolutionTwo sinusoidal waves `y_1, (x, t) and y_2(x, t)` have the same wavelength and travel together in the same direction along a string. Their amplitudes are `y_(m1)=` 4.0 mm and `y_(m2)= 3.0 mm,` and their phase constants are 0 and `pi//3` rad, respectively. What are the amplitude `y_(m)',` and phase constant of the resultant wave? Write the resultant wave in the form of Eq. 16-63.
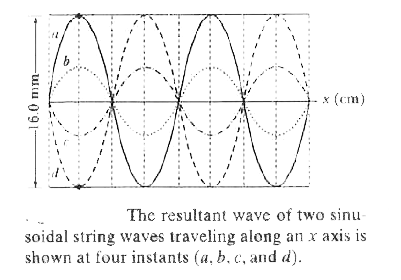
View SolutionTwo sinusoidal waves with the same amplitude and wavelength travel along a string that is stretched along an x axis, the resultant wave due to their superposition was recorded on video tape. The curves in Fig. 16-31 represent the resultant wave in four freeze frames in the sequence of a, b, c, and d, with 1.0 ms elapsing between curves a and d. The grid lines along the x axis are 1.0 cm apart, and the string elements oscillated perpendicular to the r axis by 16.0 mm (between the extreme displacements shown by curves a and d) as the resultant wave passed through them. Write equations for the two superposition waves and for their resultant wave.
View SolutionConsider a strong connected At both ends with rigid wall (Fig. 16-36). Find the second longest resonance wave length for which 3/8 is an antinode.
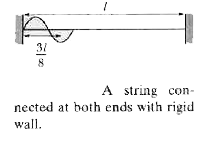
View SolutionFigure 16-37 shows resonane oscillation of a string of mass m=2.500 g and lengt L= 0.800 m and that is under tension `tau= 325.0 N`. What is the wavelength `lambda` of the transverse waves producing the standing wave patient and what is the charmant number. What is the frequency of the transverst waves and of the osciallation of the moving string elements? What is the maximum magnitude of the transverse velocity `u_(m)` of the element oscillating a coordinate x =0.180 m? At what point during the element's oscillation is the transverse velocity maximum?
View Solution
SAMPLE PROBLEM questions and complete solutions for chapter WAVES-I of RESNICK AND HALLIDAY PHYSICS (HINGLISH) of Class 12