Complete Solutions to Problems of chapter WAVES-I of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | WAVES-I |
| RESNICK AND HALLIDAY | Problems |
| Number Of Questions | 60 |
| Academic Year | 2023-24 |
A stretched string has a mass per unit length of 5.00 g/cm and a tension of 10.0 N A sinusoidal wave on this string has an amplitude of 0.16 mm and a frequency of 100 Hz and is traveling in the negative direction of an x axis. If the wave equation is of the form y(x,t)= `y_m sin(kx pm omegat),` what are (a) `y_m` (b) k. (c) `omega`, and (d) the correct choice of sign in front of `omega?`
View SolutionThe heaviest and lightest strings on a certain violin have linear densities of 3.2 and 0.26 g/m. What is the ratio of the diameter of the heaviest string to that of the lightest string, assuming that the strings are of the same material?
View SolutionA string fixed at both ends is 7.50 m long and has a mass of 0.120 kg. It is subjected to a tension of 96.0 N and set oscillating (a) What is the speed of the waves on the string? (b) What is thc longest possible wavelength for a standing wave? (c) Give the frequency of that wave.
View SolutionThe equation of a transverse wave on a string is
`y =(2.0 mm) sin[(15 m^(-1)]x -(900 s^(-1))t].` The linear density is 4.17 g/m. (a) What is the wave speed? (b) What is the tension in the string?
View SolutionTwo waves are generated on a string of length 4.0 m to produce a three-loop standing wave with an amplitude of 1.0 cm.The wave speed is 100 m/s. Let the equation for one of the waves be of the form `y(x,t) =y_m sin(kx +omegat).` In the equation for the other wave, what are (a) `y_m` (b) k, (c) `omega` and (d) the sign in front of w!
View SolutionWhat phase difference between two identical traveling waves, moving in the same direction ulung a stretched string, results in the combined wave having an amplitude 0.852 times that of the common amplitude of the two combining waves! Express your answer in (a) degrees (b) radiants, and (c) wavelengths
View SolutionA 100 g wire is held under a tension of 220 N with one end at x=0 and the other x=10.0m. At time t=0 pulse 2 is sent along the wire from the end at x=0. What position x do the pulses begin to meet?
View SolutionString A is streched between two clamps separated by distance L. String B, with the same linear density and under the same tension as string A, is stretched between two clamps separated by distance 3L eight harmonies of string B. For which of these eight har. monics of B (if any) does the frequency match the frequency of (a) A's first harmonic, (b) A's second harmonic, and (C) A sthird hannonic?
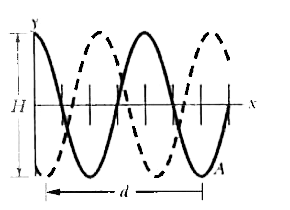
View SolutionTwo sinusoidal waves with the same amplitude of 6.00 mm and the same wavelength travel together along a string that is stretched along an x axis. Their resultant wave is shown twice in Fig. 16 39. as velley travels in the negative direction of the x axis by distance d= 56.0 cm in 8.0 ms. The lick matks along the axis are separated by 10cm, and height H is 8.0mm. Let the equation for one wive be of the form y(x,t) `=y_m sin (kx pm omegat+phi_(1))," where "phi_(1)=0` and you must choose the correct sign in front of `omega`. For the equation for the other wave, what are (a) `y_(m), (b) k, (c) omega, (d) phi_(2)`, and (e) the sign in front of `omega?`
View SolutionThe tension in a wire clamped at both ends is halved with out appreciably changing the wire length between the clamps. What is the ratio of the new to the old wave speed for transverse waves traveling along this wire?
View SolutionTwo identical traveling waves, moving in the same direction are out of phase by `0.70pi` rad. What is the amplitude of the resultant wave in terms of the common amplitude of the two combinag waves
View SolutionA rope, with mass 1.39 kg and fixed at both ends oscillates in a second-harmonic standing wave pattern. The displacement of the rope is given by
`y-(0.10m) (sin pix//2) sin 12pit`.
where x=0 at one end of the rope, x is in meters and t is in seconds. What are (a) the length of the rope, (b) the speed of the waves on the rope, and (c) the tension of the rope? (d) If the rope oscillates in a third-harmonic standing wave pattern, what will be the period of oscillation?
View SolutionA sinusoidal wave travels along a string. The time for a particular point to move from maximum placement to zero is 0.135s. What are the (a) period and (b) frequency? (c) The wavelength is 1. 40m, what is the wave speed?
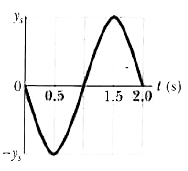
View SolutionFor a particular transverse standing wave on a long string, one of the antinodes is at r=0 and an adjacent node is at x=0.10 m. The displacement y(t) of the string particle at x =0 is shown in Fig. 16-40, where the scale of the y axis is set by `y_(s)=4.0cm.` When t = 0.50 s, what is the displacement of the string particle at (a) x= 0.20 m and (b) x= 0.30 m? What is the transverse velocity of the string particle at x =0.20 m at (c) t=0.50s and (d) t=1.0s? (e) Sketch the standing wave at t=0.50s for the range x=0 to x=0.40m.
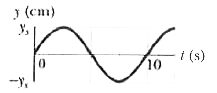
View SolutionA sinusoidal transverse wave of wavelength 18 cm travels along a string in the positive direction of an x axis. The displacement y of the string particle at x= 0) is given in Fig. 16-41 as a function of time t. The scale of the vertical axis is set by `y_1= 4.0 cm,` The wave equation is to be in the form `y(x,t)= y_(nI) sin(kx pm omega t+phi).` (a) At t= 0), is a plot of y versus x in the shape of a positive sine function on a legative sinc function? What are `(b) y_(nI) (c) k, (d) omega (e) phi`, (f) the sign in front of `omega`, and (g) the speed of the wave? (h) What is the transverse velocity of the particle at x=0 when t=5.0 s?
View SolutionTwo sinusoidal waves of the same frequency are to be sent in the same direction along a taut string. One wave has an amplitude of 5.50 mm, the other 12.0 mm. (a) What phase difference `phi_(1)` between the two waves results in the smallest amplitude of the resultant wave? (b) What is that smallest ! amplitude? (c) What phase difference `phi_(2)` results in the largest amplitude of the resultant wave? (d) What is that largest amplitude? (e) What is the resultant amplitude if the phase angle is `(phi_(1)-phi_(2))//2?`
View SolutionA nylon guitar string has a linear density of 7.20 g/m and is under a tension of 180 N. The fixed supports are distance D =90.0 cm apart. The string is oscillating in the standing wave pattern shown in Fig. 16-42. Calculate the (a) speed, (b) wavelength, and (c) frequency of the traveling waves whose superposition gives this standing wave.

View SolutionA sinusoidal wave of angular frequency 1200 rad/s and amplitude 3.00 mm is sent along a cord with linear density 4.00 g/m and tension 1200 N. (a) What is the average rate at which energy is transported by the wave to the opposite end of the cord? (b) If simultaneously, an identical wave travels along an adjacent identical cord, what is the total average rate at which energy is transported to the opposite ends of the two cords by the waves? IT, instead, those two Waves are sent along the same cuid simultaneously, what is the tolal average rate at which they transport energy when their phase difference is (c) 0, (d) `0.4pi rad`, and (e) `pi` rad?
View SolutionA generator at one end of a very long string creates a wave given by `y=(6.0 cm) cos ""pi/2 [(2.00 m^(-1)) x+(6.00 s^(-1))t]`, and a generator at the other end creates the wave
`y=(6.0 cm) cos""pi/2 [(2.00 m^(-1)) x-(6.00 s^(-1)) t]` .
Calculate the (a) frequency, (b) wavelength, and (c) speed of each wave. For `x ge 0,` what is the location of the node having the (d) smallest, (e) second smallest, and (f) third smallest value of x? For `x ge ,` what is the location of the antinode having the (g) smallest, (h) second smallest, and (i) third smallest value of x?
View SolutionA string under tension `tau_(1)` oscillates in the third harmonic at frequency `f_(3)`, and the waves on the string have wavelength `lambda_3`, If the tension is increased to `tau_(f)= 8tau_(i)`, and the string is again made to oscillate in the third harmonic, what then are (a) the frequency of oscillation in terms of `f_3` and (b) the wavelength of the waves in terms of `lambda_(3)?`
View SolutionIn Fig. 16-43, an aluminum wire, of length `L_1= 60.0 cm,` cross-sectional area `1.25 xx 10^(-2)cm^(2)` and density `2.60 "g/cm"^(3),` is joined to a steel wire, of density 7.80 g/cm`""^(3)` and the same cross-sectional area. The compound wire, loaded with a block of mass m =10.0 kg, is arranged so that the distance `L_2` from the joint to the supporting pulley is 86.6 cm. Transverse waves are set up on the wire by an external source of variable frequency: a node is located at the pulley, (a) Find the lowest frequency that generates a standing wave having the joint as one of the nodes. (b) How many nodes are observed at this frequency?

View SolutionA human wave. During sporting events within large, density packed stadiums, spectators will send a wave (or pulse) around the stadium (Fig. 16-44). As the wave reaches a group of spectators, they stand with a cheer and then sit. At any instant, the width w of the wave is the distance froin the leading edge (people are just about to stand) to the trailing edge (people have just sat down). Suppose a human wave fravels a distance of 853 seats around a stadium in 51 s, with spectators requiring about 1.8 s to respond to the wave's passage by stand- ing and then sitting. What are (a) the wave speed v in seats per second) and (b) width w (in number of sears)?

View SolutionThe linear density of a string is `1.9 xx 10^(-4)"kg/m."` A transverse wave on the string is described by the equation
`y=(0.021 m) sin[(2.0 m^(-1))x +(30 s^(-1))t].` What are (a) the wave speed and (b) the tension in the string?
View SolutionTwo sinusoidal waves with identical wavelengths and amplitudes travel in opposite directions along a string with a speed of 15 cm/s. If the time interval between instants when the string is fiat is 0.20 s, what is the wavelength of the waves?
View SolutionA string that is stretched between fixed supports separated by 75.0 cm has resonant frequencies of 450 and 308 Hz, with no intermediate resonant frequencies. What are (a) the lowest resonant frequency and (b) the wave speed?
View SolutionIf a transmission line in a cold climate collects ice, the increased diameter tends to cause vortex formation in a passing wind. The air pressure variations in the vortexes lend to cause the line to oscillate (gallop), especially if the frequency of the variations matches a resonant frequency of the line. In long lines, the resonant frequencies are so close that almost any wind speed can set up a resonant mode vigorous enough to pull down support towers or cause the line to short on with an adjacent line. If transmission line has a length of 310 m, id linear density of 3.35 kg/mı, and a tension of 90.1 MN, what are the frequency of the fundamentail made and (b) the frequency difference between sucessive modes?
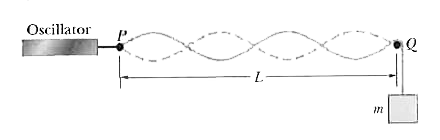
View SolutionIn Fig 16-45, a string, tied to a sinusoidal oscillator at P and running over a support at Q, is strecthed by a block of mass m, Separation, L=1,20m,l linear density `mu=1.20 g//m`, and the oscilator frequency f=120Hz. The amplitude of the motion at P is small enough for that point to be considered a node. A node also exists at Q. (a) What mass m allows the osciallator to set up the fourth harmonic on the string? (b) What standing wave mode, if any can be set up if m=1.00kg?
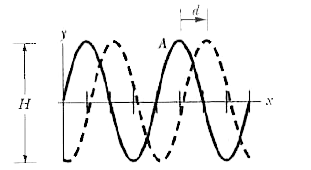
View SolutionIn Fig 16-46, a sinusoidal wave moving along a string is shown twice as crest A travels in the positive direction of any x axis by distance d=6.0 cm in 3.0 ms. The tick marks along the axis are separated by 10cm, height H=6.00MM. The equation for the wave is in the form y(x,t) =`y_(m) sin (kx pm omegat)`. so what are (a) `y_(m), (b) k, (c) omega` and (d) the correct choice of sign in front of `omega?`
View SolutionIn Fig. 16-45, a string, tied to a sinusoidal oscillator at P and running over a support at Q, is stretched by a block of mass m. The separation L between P and Q is 1.20 m, and the frequency f of the oscillator is fixed at 120 Hz. The amplitude of the motion at P is small enough for that point to be considered a node. A node also exists at Q. A standing wave appears when the mass of the hanging block is 286.1 g or 4470g, but not for any intermediate mass. What is the linear density of the string?
View SolutionA sinusoidal wave of frequency 500 Hz has a speed of 320 m/s. (a) How far apart are two points that differ in phase by `pi//3` rad? (b) What is the phase difference between two displacements at a certain point at times 1.00 ms apart?
View SolutionUse the wave equation to find the speed of a wave given by `y(x,t) =(3.00 mm) sin [(3.00 m^(-1)) x-(8.00 s^(-1))t])`.
View SolutionA string has mass 200 g. Wave speed 120 m/s, and tension 700N (a)What is its length? (b) What is the lowest resonant frequency of this string?
View SolutionOne of the harmonic frequencies for a particular string under tension is 310 Hz. The next higher harmonic frequency is 400 Hz. What harmonic frequency is next higher after the hannonc frequency 850 Hz?
View SolutionIn fig. 16-47a, string 1 has a linear density of 3.00 g/m, and string 2 has a linear density of 5.00 g/m. They are under tension due to the hanging block of mass M= 800 g. Calculate the wave speed on (a) string 1 and (b) string 2 (Hint: When a string loops halfway around a pulley, it pulls on the pulley witii a net force that is twice the tension in the string) Next the block is divided into two blocks (with `M_(1)+M_(2)=M)` and the apparatus in tearranged as shown in fig. 16-47b. Find (c) `M_(1) and (d) M_(2)` such that the wave speeds in the two strings are equal.

View SolutionTwo sinusoidal waves of the same frequency travel in the same direction along a string. If `y_(m1) =2.0 cm, y_(m2)=4.0cm , phi_(1)=0, and phi_(2)=pi//2 rad`, what is the amplitude of the resultant wave?
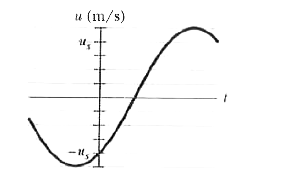
View SolutionFigure 16-48 shows the transverse velocity u versus time t of the point on a string at x=0, as a wave passes through it. The scale on the vertical axis is set by `u_(s)=12m//s`. The wave has the generic form y(x,t)= `y_(m) sin (kx-omegat+phi)`. What them is `phi?`
View SolutionThese two waves travel along the same string:
`y (x,t)= (4.00 mm) sin(2pi x - 650pit)`
`y_2(x,t) =(6.20 mm) sin(2npi- 650pit +0.60x rad).` What are (a) the amplitude and (b) the phase angle (relative to wave 1) of the resultant wave? (c) If a third wave of amplitude 5.00 mm is also to be sent along the string in the same direction as the first two waves, what should be its phase angle in order to maximize the amplitude of the new resultant wave?
View SolutionA standing wave pattern on a string is described by
`y(x,t) =0.040 (sin 4pi x) (cos 4pi t)`.
where x and y are in meters and r is in seconds For `x ge 0` what is the location of the node with the (a) smallest, (b) second smallest, and (c) third smallest value of x? (d) What is the period of the oscillatory motion of any (nonnode) point? What are the (e) speed and (f) amplitude of the two traveling waves that interfere to produce this wave? For `t gt 0,` what are the (g) first, (h) second, and (i) third time that all points on the string have zero transverse velocity?
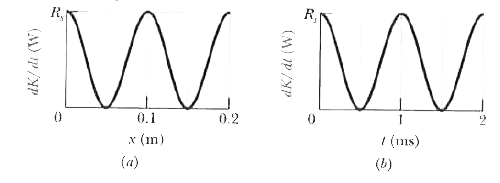
View SolutionA sinusoidal wave is sent along a string with a linear density of 5.0 g/m. As it travels, the kinetic energies of the mass elements along the string vary Figure 10-49a gives the rate dk/dt at which kinetic energy passes through the string elements at a particular instant, plotted as a function of distance x along the string. Figure 1649b is similar except that it gives the rate at which kinetic energy passes through a particular mass element at a particular location) plotted as a function of time. For botle figures the scale in the vertical (rate) axis is set by `R_s=10W`. What is the amplitude of the wave?
View SolutionThe equation of a transverse wave traveling along a very long string is y 3.0 sin `(0.020pi x -4.0pit),` where x and y are expressed in contimeters and t is in seconds. Determine (a) the amplitude. (b) the wavelength, (c) the frequency (d) the speed, (e) the direction of propagation of the wave, and (f) the maximum transverse speed of a particle in the string (g) What is the transverse displacement at x=3.5 cm when 0.26s ?
View SolutionWhat is the speed of a transverse wave in a rope of length 1.75 m and mass 60.0 g under a tension of 500 N?
View SolutionThe function y(x,t) =(15.0 cm) `cos(pi x-15pit),` with x in meters and t in seconds, describes a wave on a taut string. What is the transverse speed for a point on the string at an instant when that point has the displacement y= +6.00 cm?
View SolutionWhat are (a) the lowest frequency. (b) the second lowest frequency, and (c) the third lowest frequency for standing waves on a wire that is 10.0 m long, has a mass of 100 g. and is stretched under a tension of 275 N?
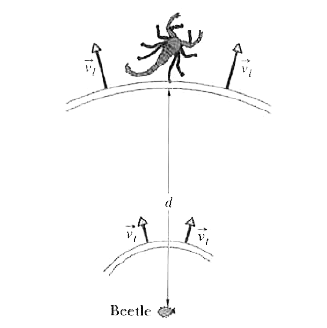
View SolutionA sand scorpion can detect the motion of a nearby beetle (its prey) by the waves the motion sends along the sand surface (Fig, 16-50). The waves are of two types transverse waves traveling at `v_(1)= 50` m/s and longitudinal waves traveling at `V_(1)=150 m//s`. If a sudden motion sends out such waves a scorpion can tell the distance of the bestle from the difference ar in the arrival times of the waves at its leg nearest the beetle. What is that time difference if the distance beetle is 37.5 cm?
View SolutionTwo sinusoidal waves of the same period, with amplitudes of 5.0 and 7.0 mm, travel in the same direction along a stretched string, they produce a resultant wave with an amplitude of 10.0 mm. The phase constant of the 5.0mm wave is 0. What is the phase constant of the 7.0mm wave?
View SolutionFour waves are to be sent along the same string, in the same direction :
`y_(1) (x,t)=(5.00 mm) sin (4pi x-400pit)`
`y_(2) (x,t) =(5.00 mm) sin (4pi x-400 pit+0.8pi)`
`y_(3) (x,t) =(5.00 mm) sin (4pi x-400pit+pi)`
`y_(4) (x,t)=(5.00 mm) sin (4pi x-400 pit+1.8pi)`
What is the amplitude of the resultant wave?
View SolutionIf a wave y(x,t)=(5.0 mm) sin(kr +(600 rad/s) `t+phi)` travels along a string, how much time does any given point on the string take to move between displacements y=+2.0 mm and y=-2.0 mm?
View SolutionA string along which waves can travel is 2.70 m long and has a mass of 130 g. The tension in the string is 36.0 N What must be the frequency of traveling waves of amplitude 7.70 mm for the average power to be 170 W?
View SolutionA uniform rope of mass m and length L hangs from a ceiling. (a) Show that the speed of a transverse wave on the rope is a function of y, the distance from the lower end, and is given by `v=sqrt(gy)`. (b) Show that the time a transverse wave takes to travel the length of the rope is given by `t=2 sqrt(L//g)`.
View SolutionThe speed of a transverse wave on a string is 115 m/s when the string tension is 200 N. To what value must the tension be changed to raise the wave speed to 223 m/s?
View SolutionA sinusoidal transverse wave is traveling along a string in the negative direction of an x axis. Figure 16-S1 shows a plot of the displacement as a function of position at time t = 0, the scale of the y axis is set by y = 4.0 cm. The string tension is 3.6 N, and its linear density is 28 g/m. Find the (a) amplitude, (b) wavelength, (e) wave speed, and (d) period of the wave (e) Find the maximum transverse speed of a particle in the string. If the wave is of the form `y(x,t) =y_(m) sin (kx pm omega t+phi)`, what are (f) k, (g) `omega (h) phi`, and (i) the correct choice of sign in front of `omega?`

View SolutionUse the wave equation to find the speed of a wave given in terms of the general function h(x,t):
`y(x,t) =(4.00 mm) sin[(22.0 m^(-1)) x+(8.00 s^(-1)t]` .
View SolutionA transverse sinusoidal wave is moving along a string in the opposite direction of an x axis with a speed of 70m/s. At t=0 the string particle at x=0 has a transverse displacement of 4.0 cm and is not moving. The maximum transverse speed of the string particle at x=0 is 16m/s. (a) What is the frequency of the wave? (b) What is the wavelength of the wave? If y(x,t) `=y_(m) sin (kx pm omega t+phi)` is the form of the wave equation, what are (c) `y_(m), (d) k, (e) omega (f) phi`, and (g) the correct of sign in front of `omega?`
View SolutionA sinusoidal wave travels along a string under tension. Figure 16-52 gives the slopes along the string at time t=0. The scale of the x axis is st by `x_(s)=0.40`m What is the amplitude of the wave?
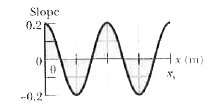
View SolutionA string oscillates according to the equation
`y' = (0.50 cm) sin [((pi)/(3)cm^(-1))x] cos [(40 pi s^(-1))t]`.
What are the (a) amplitude and (b) speed of the two waves (identical except for direction of travel) whose superposition gives the oscillation? (c) what ist eht distance between nodes? (d) What is the transverse speed of particle of the string at the position `x = 1.5 cm` when `t = (9)/(8)s`?
View SolutionTwo sinusoidal waves with the same amplitude and wavelength travel through each other along a string that is stretched along an x axis. Their resultant wave is shown twice in Fig. 16-53, as the antinode A travels from an extreme upward displacement to an extreme downward displacement in 6.0 ms. The tick marks along the axis are separated by 15 cm, height H is 1.20 cm. Let the equation for one of the two waves be of the form `y(x, t) =y_(m) sin(kx + omega).` In the equation for the other wave, what are `(a) y_(m) (b) k, (c) omega,` and (d) the sign in front of `omega`?

View SolutionA 40 cm wire having a mass of 3.2 g is stretched between two fixed supports 40.05 cm apart. In its fundamental mode, the wire vibrates at 220 Hz. If the area of cross section of the wire is `1.0 mm^2`, find its Young modulus.
View SolutionA string, fixed at both ends, vibrates in a resonant mode with a separation of 2.0 cm between the consecutive nodes. For the next higher resonant frequency, this separation is reduced to 1.6 cm. Find the length of the string.
View SolutionFigure 16-54 shows the displacement y versus time t of the point on a string at x=0, as a wave passes through that point. The scale of the y axis is set by `y_(s)=6.0 mm`. The wave has form `y(x,t)=y_(ln) sin (kx-omega t+phi)." What is the "phi?`

View SolutionFigure shows an aluminium wire of length `60 cm` joined to a steel wire of length `80 cm` and stretched between two fixed supports. The tension produced is `40 N`. The cross-sectional area of the steel wire is `1.0 mm^(2)` and that of the aluminimum wire is `3.0 mm^(2)` The minimum frequency of a tuning fork which can produce standing waves in the system with the joint as a node is `10P` (in `Hz`) the find `P`. Given density of aluminimum is `2.6 g//cm^(3)` and that of steel is `7.8 g//cm^(3)`.

View Solution
Problems questions and complete solutions for chapter WAVES-I of RESNICK AND HALLIDAY PHYSICS (HINGLISH) of Class 12