Complete Solutions to PROBLEMS of chapter INTERFERENCE AND DIFFRACTION of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | INTERFERENCE AND DIFFRACTION |
| RESNICK AND HALLIDAY | PROBLEMS |
| Number Of Questions | 61 |
| Academic Year | 2023-24 |

In Figure, a broad bcam Incident light of light of wavelength 630 nn is sent directly downward through the top plate of a pair of glass plates touching at the left end. The air between the plates acts as a thin film, and an interference pattern can be seen from above the plates. Initially, a dark fringe lies at the left end, a bright fringe lies at the right end, and nine dark fringes lie between those two end fringes. The plates are then very gradually squeezed together at a constant rate to decrease the angle between them. As a result, the fringe at the right side changes between being bright to being dark every 15.0 s. (a) At what rate is the spacing between the plates at the right end being changed? (b) By how inuch has the spacing there changed when both left and right ends have a dark fringe and there are five dark fringes between them?
View Solution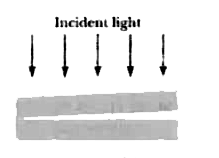
In Figure, two microscope slides touch at one end and are separated at the other end. When light of wavelength 420 nm shines vertically down on the slides, an overhead observer sees an interference pattern on the slides with the dark fringes separated by 1.9 mm. What is the angle between the slides?
View Solution
Two waves of light in air, of wavelength `lambda= 600.0 nm`, are initially in phase. They then both travel through a layer of plastic as shown in Figure, with `L_(1)= 4.00 mu m, L_(2)= 3.50 mu m, n_(1) = 1.42`, and `n_(2) = 1.60.` (a) What multiple of `lambda` gives their phase difference after they both have emerged from the layers? (b) If the waves later arrive at some common point with the same amplitude, is their interference fully constructive, fully destructive, interme- diate but closer to fully constructive, or intermediate but closer to fully destructive?
View SolutionThe wavelength of yellow sodium light in air is 589 nm. (a) What is its frequency? (b) What is its wavelength in glass whose index of refraction is 1.52? (c) From the results of (a) and (b), find its speed in this glass.
View SolutionTwo waves of the same frequency have amplitudes 1.60 and 2.20. They interfere at a point where their phase difference is `60.0^(@)`. What is the resultant amplitude?
View SolutionA double-slit arrangement produces interference fringes for sodium light (`lambda= 589 nm`) that have an angular separation of `3.50 xx 10^(-3)` rad. For what wavelength would the angular separation be 6.0% greater?
View SolutionWhite light is sent downward onto a horizontal thin film that is sandwiched between two materials. The indexes of refraction are 1.80 for the top material, 1.65 for the thin film, and 1.50 for the bottom material. The film thickness is `5.00 xx 10^(-7)` m. Of the visible wavelengths (400 nm to 700 nm) that result in fully constructive interference at an observer above the film, which is the (a) longer and (b) shorter wavelength? The materials and film are then heated so that the film thickness increases. (c) Does the light resulting in fully constructive interference shift toward longer or shorter wavelengths?
View SolutionIn a double slit experiment, the distance between the slits is 5.0 mm and the slits are 1.0m from the screen. Two interference patterns can be seen on the screen one due to light with wavelength 480nm, and the other due to light with wavelength 600nm. What is the separation on the screen between the third order bright fringes of the two intergerence patterns?
View SolutionIn Figure, a light ray is incident at angle `theta_(1)= 55^(@)` on a series of five transparent layers with parallel boundaries. For layers 1 and 3. `L_(1) = 20 mu m, L_(3) = 25 mu m, n_(1) = 1.6`, and `n_(3) = 1.15`. (a) At what angle does the light emerge back into air at the riglit? (b) How much time does the light take to travel through layer 3?

View SolutionAssume that two waves of light in air, of wavelength 585 nm, are initially in phase. One travels through a glass layer of index of refraction `n_(1) = 160` and thickness L. The other travels through an equally thick plastic layer of index of refraction `n_(2)= 1.50`. (a) What is the smallest value L should have if the waves are to end up with a phase difference of 5.65 rad? (b) If the waves arrive at some common point with the same amplitude, is their interference fully constructive, fully destructive, intermediate but closer to fully constructive, or intermediate but closer to fully destructive?
View SolutionThe rhinestones in costume jewelry are glass with index of refraction 1.50. To make uliem more reflective, they are often coated with a layer of silicon monoxide of index of refraction 2.00. What is the minimum coating thickness nccded to ensure that light of wavelength 500 nm and of perpendicular incidence will be reflected from the two surfaces of the coating with fully constructive interference?
View SolutionA disabled tanker leaks kerosene (n = 1.20) into the Persian Gulf, creating a large slick on top of the water (n = 1.30). (a) If you are looking straight down from an airplane, while the Sun is overhead, at a region of the slick where its thickness is 380 nm, for which wavelength(s) of visible light is the reflection brightest because of constructive interference? (b) If you are scuba diving directly under this same region of the slick, for which wavelength(s) of visible light is the transmitted intensity strongest?
View SolutionA thin film (n = 1.25) coats a thick glass plate (n = 1.50). White light is incident normal to the film. In the reflections, fully destructive interference nccurs at 600 mm and fully constructive interference at 700 nm. Calculate the thickness of the film.
View Solution
In Figure, a light wave along ray `r_(1)` reflects once from a mirror and a light wave along ray `r_(2)` reflects twice from that same mirror and once from a tiny mirror at distance L from the bigger mirror. (Neglect the slight tilt of the rays.) The waves have wavelength 350 nm and are initially in phase. (a)What is the smallest value of L that puts the final light waves exactly out of phase? (b) With the tiny mirror initially at that value of L, how far must it be moved away from the bigger mirror to again put the final waves out of phase?
View Solution
In Figure, a light wave along ray `r_(1)` reflects once from a mirror and a light wave along ray `r_(2)` reflects twice from that same mirror and once from a tiny mirror at distance L from the bigger mirror. (Neglect the slight tilt of the rays.) The waves have wavelength `lambda` and are initially exactly out of phase. What are the (a) smallest. (b) second smallest, and (c) fourth smallest values of `L // lambda` that result in the final waves being exactly in phase?
View SolutionIn the double-slit experiment, the viewing screen is at distance D = 4.00 m, point P lies at distance y = 20.5 cm from the center of the pattern, the slit separation d is `4.50 mu m`, and the wavelength `lambda` is 650 nm. (a) Determine where point P is in the interference pattern by giving the maximum or minimum on which it lies, or the maximum and minimum between which it lies. (b) What is the ratio of the intensity `I_(P)` at point P to the intensity `I_("cen")` at the center of the pattern?
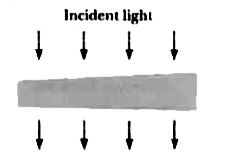
View SolutionIn Figure, a broad beam of light of wavelength 420 nm is incident at `90^(@)` on a thin, wedge-shaped film with index of refraction 1.70. Transmission gives 10 bright and 9 daik fringes along the film's length. What is the left- to-right change in film thickness?
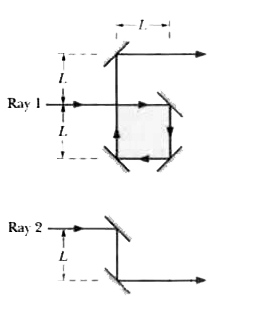
View SolutionIn Figure, two light rays go through different paths by reflecting from the various flat surfaces shown. The light waves have a wavelength of 411.0 nm and are initially in phase. What are the (a) smallest and (b) second smallest value of distance L that will put the waves exactly out of phase as they emerge from the region?
View SolutionWe wish to coat flat glass (n=1.50) with a transparent material (n = 1.45) so that reflection of light at wavelength 500 nm is eliminated by interference. What minimum thickness can the coating have to do this?
View SolutionA plane wave of monochromatic light is incident normally on a uniform thin film of oil that covers a glass plate. The wavelength of the source can be varied continuously. Fully destructive interference of the reflected light is observed for wavelengths of 500 nm and 700 nm and for no wavelengths in between. If the index of refraction of the oil is 1.26 and that of the glass is 1.50, find the thickness of the oil film.
View SolutionAssume that the two light waves, of wavelength 515 nm in air, are initially out of phase by `pi` rad. The indexes of refraction of the media are `n_(1)=1.45` and `n_(2)= 1.75`. What are the (a) smallest and (b) second smallest value of L that will put the waves exactly in phase once they pass through the two media?
View SolutionIn a double-slit experiment, the fourth-order maximum for a wavelength of 450 nm occurs at an angle of `theta= 90^(@)`. (a) What range of wavelengths in the visiblc range (400 nm to 700 nm) are not present in the third-order maxima? To eliminate all visible light in the fourth-order maximum, (b) should the slit separation be increased or decreased and (c) what least change is needed?
View SolutionLight of wavelength 424 nm is incident perpendicularly on a soap film (n = 1.33) suspended in air. What are the (a) least and (b) second least thicknesses of the film for which the reflections from the film undergo fully construc- tive interference?
View SolutionIn the double-slit experiment, the electric fields of the waves arriving at point P are given by
`E_(1)=(2.00 mu V // m)sin[(1.26 xx 10^(15))t]`
`E_(2)=(2.00 mu V // m)sin[(1.26=10^(15))t+38.6 "rad"]`
where timer is in seconds. (a) What is the amplitude of the resultant electric field at point P? (b) What is the ratio of the intensity `I_(P)` at point P to the intensity `I_("cen")` at the center of the interference pattern? (C) Describe where point P is in the interference pattern by giving the maximum or minimum on which it lies, or the maximum and minimum between which it lies. In a phasor diagram of the electric fields, (d) at what rate would the phasors rotate around the origin and (e) what is the angle between the phasors?
View SolutionThree electromagnetic waves travel through a certain point P along an x axis. They are polarized parallel to a y axis, with the following variations in their amplitudes. Find their resultant at P.
`E_(1)=(8.00 mu V // m)sin[(2.0 xx 10^(14) "rad" // s)t]`
`E_(2)=(5.00 mu V // m)sin[(2.0 xx 10^(14) "rad" // s)t+55.0^(@)]`
`E_(3)=(5.00 mu V // m)sin[(2.0 xx 10^(14) "rad" // s)t-55.0^(@)]`
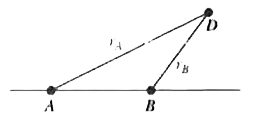
View SolutionIn Figure, sources A and B emit long-range radio waves of wavelength 400 m, with the phase of the emission from A ahead of that from source B by `90.0^(@)`. The distance `r_(A)` from A to detector D is greater than the corresponding distance `r_(B)` by 150 m. What is the phase difference of the waves at D?
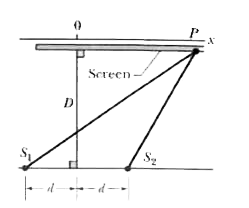
View SolutionIn Figure, two isotropic point sources `S_(1)` and `S_(2)` emit light in phase at wavelength `lambda` and at the same amplitude. The sources are separated by distance `2d = 6.00 lambda`. They lie on an axis that is parallel to an x axis, which runs along a viewing screen at distance `D = 20.0 lambda`. The origin lies on the perpendicular bisector between the sources. The figure shows two rays reaching point P on the screen, at position `x_(P)`. (a) At what value of `x_(P)` do the rays have the minimum possible phase difference? (b) What multiple of `lambda` gives that minimum phase difference? (c) At what value of `x_(P)` do the rays have the maximum possible phase difference? What multiple of `lambda` gives (d) that maximum phase difference and (c) the phase difference when `x_(P)=6.00 lambda`? (f) When `x_(P)=6.00 lambda`, is the resulting intensity at point P maximum, minimum, intermediate but closer to maximum, or intermediate but closer to minimum?
View SolutionSuppose that the two waves have wavelength `lambda= 610 nm` in air. What multiple of `lambda` gives their phase difference when they emerge if (a) `n_(1) = 1.50, n_(2) = 1.60`, and L = 700 um, (b) `n_(1)= 1.62, n_(2) = 1.72`, and L = 700 um, and (c) `n_(1) = 1.83, n_(2) = 1.59`, and L = 2.16 um? (d) Suppose that in each of these three situations the waves arrive at a common point (with the same amplitude) after emerging, Rank the situations according to the brightness the waves produce at the common point.
View SolutionMonochromatic green light, of wavelength 550 nm, illuminates two parallel narrow slits `5.60 mu m` apart. Calculate the angular deviation of the third-order (m=3) bright fringe (a) in radians and (b) in degrees.
View SolutionA thin flake of mica (n = 1.58) is used to cover one slit of a double-slit interference arrangement. The central point on the viewing screen is now occupied by what had been the fifth bright side fringe (m = 5). If `lambda= 550 nm`, what is the thickness of the mica?
View SolutionIn a double-slit arrangement the slits are separated by a distance equal to 100 times the wavelength of the light passing through the slits. (a) What is the angular separation in radians between the central maximum and an adjacent maximum? (b) What is the distance between these maxima on a screen 90.0 cm from the slits?
View SolutionA double-slit arrangement produces interference fringes for sodium light (`lambda=589 nm`) that are `0.25^(@)` apart. What is the angular separation if the arrangement is immersed in water (n=1.33)?
View Solution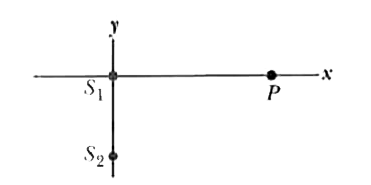
In Figure, two isotropic point sources of light (`S_(1)` and `S_(2)`) are separated by distance `2.70 mu m` along a y axis and emit in phase at wavelength 900 nm and at the same amplitude. A light detector is located at point P at coordinate `x_(P)` on the x axis. What are (a) the greatest value of `x_(P)` and (b) the second greatest value at which the detected light is minimum due to destructive interference?
View Solution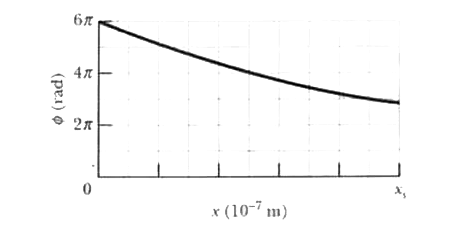
Figure shows two isotropic point sources of light (`S_(1)` and `S_(2)`) that emit in phase at wavelength 400 nm and at the same amplitude. A detection point P is shown on an x axis that extends through source `S_(1)`. The phase difference `phi` between the light arriving at point P from the two sources is to be measured as P is moved along the x axis from x = 0 out to `x= + infty`. The results out to `x_(s) = 10 xx 10^(-7)` m. On the way out to `+ infty`, what is the greatest value of x at which the light arriving at P from `S_(1)` is exactly out of phase with the light arriving at P from `S_(2)` ?

View Solution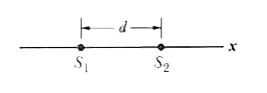
In Figure, two radio- frequency point sources `S_(1)` and `S_(2)` separated by distance d = 1.8 m, are radiating in phase with `lambda = 0.50 m`. A detector moves in a large circular path around the two sources in a plane contain- ing them. How many (a) maxima and (b) minima does it detect?
View SolutionThe ratio of intensitics duc to upper and lower slits on the screen of a Young's double-slit experiment is 16:9. Find the ratio of maximum to average intensity on screen.
View SolutionIn a Young's double-slit experiment apparatus, two identical slits are separated by 1 mm and distance between slits and screen is 1 m. The wavelength of light used is 6000 Å. What is the minimum distance between two points on the screen having 75% intensity of the maximum intensity?
View SolutionTwo coherent point sources `S_(1)` and `S_(2)` are located at a distance 4l from each other. Perpendicular to the straight line joining `S_(1)` and `S_(2)` there is a large screen at a distance of 1000 `lambda` from `S_(1)` as shown in Figure. Find the radius of the third maxima starting from the point 0.
View SolutionThe distance between a slit and a biprism of acute angle `2^(@)` is 10 cm. Find (a) the fringe width and (b) the width of the entire fringe pattern when observation is made on screen at a distance of 90 cm from the biprism. The refractive index of the biprism is 1.5 and l = 5890 Å.
View SolutionEstimate the linear separation of two objects on Mars that can just be resolved under ideal conditions by an observer on Earth (a) using the naked eye and (b) using the 200 in. (= 5.1 m) Mount Palomar telescope. Use the following data: distance to `"Mars" = 8.0 xx 10^(7)` km, diameter of pupil = 5.0 mm, wavelength of light = 550 nm.
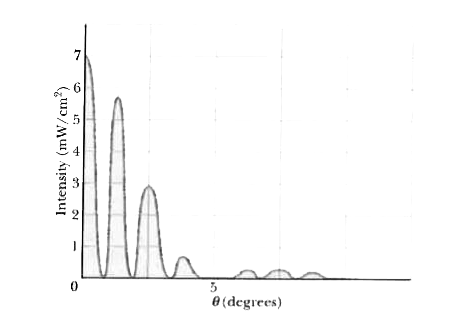
View SolutionLight of wavelength 620 nm passes through a double slit, yielding a diffraction pattern whose graph of intensity l versus angular position `theta` is shown in Figure. Calculate (a) the slit width and (b) the slit separation. (c) Verify the displayed intensities of thc m = 1 and m = 2 interference fringes.
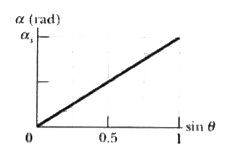
View SolutionFigure gives `alpha` versus the sine of the angle `theta` in a single-slit diffraction experiment using light of wavelength 610 nm. The vertical axis scale is set by `alpha_(s) = 12` rad. What are (a) the slit width, (b) the total number of diffraction minima in the pattern (count them on both sides of the center of the diffraction pattern), (e) the least angle for a minimum, and (d) the greatest angle for a minimum?
View SolutionSound waves with frequency 2500 Hz and speed `343 m // s` diffract through the rectangular opening axis of a speaker cabinet and into a large auditorium of length d = 100 m. The opening, which has a horizontal width of 30.0 cm, faces a wall 100 m away. Along that wall, how far from the central axis will a listener be at the first diffraction minimum and thus have difficulty hearing the sound? (Neglect reflections.)

View Solution(a) How many bright fringes appear between the first diffraction-envelope minima to either side of the central maximum in a double-slit pattern if `lambda 550 nm`, d = 0.180 mm, and `a = 30.0 mu m`? (b) What is the ratio of the intensity of the third bright fringe to the intensity of the central fringe?
View SolutionA single slit is illuminated by light of wavelengths `lambda_(a)` and `lambda_(b)` chosen so that the first diffraction minimum of the `lambda_(a)` component coincides with the second minimum of the `lambda_(b)` component. (a) If `lambda_(b)= 420 nm`, what is `lambda_(a)`? For what order number `m_(b)` (if any) does a minimum of the `lambda_(b)` component coincide with the minimum of the `lambda_(a)` component in the order number (b) `m_(a) = 2` and (c) `m_(a) = 3`?
View SolutionA slit 1.00 mm wide is illuminated by light of wavelength 650 nm. We see a diffraction pattern on a screen 3.00 m away. What is the distance between the first and third diffraction minima on the same side of the central diffraction maximum?
View SolutionThe two headlights of an approaching automobile are 1.4 m apart. At what (a) angular separation and (b) maximum distance will the eye resolve them? Assume that the pupil diameter is 4.5 mm, and use a wavelength of 550 nm for the light. Also assume that diffraction effects alone limit the resolution so that Rayleigh's criterion can be applied.
View SolutionA 0.20 mm wide slit is illuminated by light of wave- length 420 nm. Consider a point P on a viewing screen on which the diffraction pattern of the slit is viewed, the point is at `30^(@)` from the central axis of the slit. What is thc phase difference between the Huygens wavelets arriving at point P from the top and midpoint of the slit?
View SolutionIn conventional television, signals are broadcast from towers to home receivers. Even when a receiver is not in direct view of a tower because of a hill or building, it can still intercept a signal if the signal diffracts enough around the obstacle, into the obstacle's "shadow region." Previously, television signals had a wavelength of about 50 cm, but digital television signals that are transmitted from towers have a wavelength of about 10 mm. (a) Did this change in wavelength increase or decrease the diffraction of the signals into the shadow regions of obstacles? Assume that a signal passes through an opening of 6.0 m width between two adjacent buildings. What is the angular spread of the central diffraction maximum out to the first minima) for wavelengths of (b) 50 cm and (c) 10 mm?
View SolutionEntoptic halos. If someone looks at a bright outdoor lamp in otherwise dark surroundings, the lamp appears to be surrounded by bright and dark rings (hence halos) that are actually a circular diffraction pattern, with the central maximum overlapping the direct light from the lamp. The diffraction is produced by structures within the cornea or lens of the eye (hence entoptic). If the lamp is monochromatic at wavelength 550 nm and the first dark ring subtends angular diameter `2.0^(@)` in the observer's view, what is the linear) diameter of the structure producing the diffraction?
View SolutionIn the single-slit diffraction experiment, let the wavelength of the light be 500 nm, the slit width be 6.00 `mu`m, and the viewing screen be at distance D=4.00 m. Let a y axis extend upward along the viewing screen, with its origin at the center of the diffraction pattern. Also let `I_(P)` represent the intensity of the diffracted light at point P at y = 15.0 cm (a) What is the ratio of `I_(P)` to the intensity `I_(m)` at the center of the pattern? (b) Determine where point P is in the diffraction pattern by giving the maximum and minimum between which it lies, or the two minima between which it lies.
View SolutionA plane wave of wavelength 420 nm is incident on a slit with a width of a=0.60 mm. A thin converging lens of focal length +70 cm is placed between the slit and a viewing screen and focuses the light on the screen. (a) How far is the screen from the lens? (b) What is the distance on the screen from the center of the diffraction pattern to the first minimum?
View SolutionAssume that Rayleigh's criterion gives the limit of resolution of an astronaut's eye looking down on Earth's surface from a typical space shuttle altitude of 420 km. (a) Under that idealized assumption, estimate the smallest linear width on Earth's surface that the astronaut can resolve. Take the astronaut's pupil diameter to be 5 mm and the wavelength of visible light to be 550 nm. (b) Can the astronaut resolve the Great Wall of China, which is more than 3000 km long, 5 to 10 m thick at its base, 4 m thick at its top, and 8 min height? (c) Would the astronaut be able to resolve any unmistakable sign of intelligent life on Earth's surface?

View Solution(a) Show that the values of a at which intensity maxima for single-slit diffraction occur can be found exactly by differentiating Eq. 35-56 with respect to `alpha` and equating the result to zero, obtaining the condition `tan alpha= alpha`. To find values of a satisfying this relation, plot the curve `y = tan alpha` and the straight line `y = alpha` and then find their intersections, or use a calculator to find an appropriate value of `alpha` by trial and error. Next, from `alpha = (m + 1 // 2)pi`, determine the values of m associated with the maxima in the single-slit pattern. (These m values are not integers because secondary maxima do not lie exactly halfway between minima.) What are the (b) smallest `alpha` and (c) associated m, the (d) second smallest `alpha` and (e) associated m, and the (f) third smallest `alpha` and (g) associated m?
View SolutionThe telescopes on some commercial surveillance satellites can resolve objects on the ground as small as 85 cm across (see Google Earth), and the telescopes on military surveillance satellites reportedly can resolve objects as small as 10 cm across. Assume first that object resolution is determined entirely by Rayleigh's criterion and is not degraded by turbulence in the atmosphere. Also assume that the satellites are at a typical altitude of 420 km and that the wavelength of visible light is 550 nm. What would be the required diameter of the telescope aperture for (a) 85 cm resolution and (b) 10 cm resolution? (c) Now, considering that turbulence is certain to degrade resolution and that the aperture diameter of the Hubble Space Telescope is 2.4 m, what can you say about the answer to (b) and about how the military surveillance resolutions are accomplished?
View SolutionLight of wavelength 420 nm is incident on a narrow slit. The angle between the first diffraction minimum on one side of the central maximum and the first minimum on the other side is `2.00^(@)`. What is the width of the slit?
View Solution(a) A circular diaphragm 50 cm in diameter oscillates at a frequency of 25 kHz as an underwater source of sound used for submarine detection, Far from the source, the sound intensity is distributed as the diffraction pattern of a circular hole whose diameter equals that of the diaphragm. Take the speed of sound in water to be `1450 m // s` and find the angle between the normal to the diaphragm and a line from the diaphragm to the first minimum. (b) Is there such a minimum for a source having an (audible) frequency of 1.0 kHz?
View SolutionMonochromatic light of wavelength 441 nm is incident on a narrow slit. On a screen 2.00 m away, the distance between the second diffraction minimum and the central maximum is 1.80 cm.(a) Calculate the angle of diffraction `theta` of the second minimum. (b) Find the width of the slit.
View SolutionMonochromatic light with wavelength 420 nm is incident on a slit with width 0.050 mm. The distance from the slit to a screen is 3.5 m. Consider a point on the screen 2.2 cm from the central maximum. Calculate (a) `theta` for that point, (b) `alpha`, and (c) the ratio of the intensity at that point to the intensity at the central maximum.
View SolutionTwo slits of width a and separation d are illuminated by a coherent beam of light of wavelength `lambda`. What is the linear separation of the bright interference fringes observed on a screen that is at a distance D away?
View Solution(a) In a double-slit experiment, what ratio of d to a causes diffraction to eliminate the fourth bright side fringe? (b) what other bright fringes are also eliminated?
View Solution
PROBLEMS questions and complete solutions for chapter INTERFERENCE AND DIFFRACTION of RESNICK AND HALLIDAY PHYSICS (HINGLISH) of Class 12