Complete Solutions to SAMPLE PROBLEM of chapter INTERFERENCE AND DIFFRACTION of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | INTERFERENCE AND DIFFRACTION |
| RESNICK AND HALLIDAY | SAMPLE PROBLEM |
| Number Of Questions | 24 |
| Academic Year | 2023-24 |
In Fig. , the two light waves that are represented by the rays have wavelength 550.0 nm before entering media 1 and 2. They also have equal amplitudes and are in phase. Medium 1 is now just air, and medium 2 is a transparent plastic layer of index of refraction 1.600 and thickness 2.600 `mu`m.
What is the phase difference of the emerging waves in wavelengths, radians, and degrees? What is their effective phase difference (in wavelengths)?
View SolutionIn Fig. , the two light waves that are represented by the rays have wavelength 550.0 nm before entering media 1 and 2. They also have equal amplitudes and are in phase. Medium 1 is now just air, and medium 2 is a transparent plastic layer of index of refraction 1.600 and thickness 2.600 `mu`m.
If the waves reached the same point on a distant screen, what type of interference would they produce?
View SolutionWhat is the distance on screen C in Fig. 35-11a between adjacent maxima near the center of the interference pat- tern? The wavelength `lambda` of the light is 546 nm, the slit separation d is 0.12 mm, and the slit-screen separation D is 55 cm. Assume that `theta` in Fig. 35-11 is small enough to permit use of the approximations `sin theta ~~ tan theta ~~ theta`, in which `theta` is expressed in radian measure.
View SolutionYoung's double slit experiment is performed inside water `(mu = 4/3)` with light of frequency `6 xx 10^(14)` Hz. If the slits are separated by 0.2 mm and the screen kept 1 m from the slits, find the fringe width. Using the same set-up, what will the fringe width be if the experiment is performed in air?
View SolutionA coherent parallel beam of microwaves of wavelength `lambda = 0.5 mm` falls on aYoung's double- slit apparatus. The separation between the slits is 1.0 mm. The intensity of microwaves is measured on a screen placed parallel to the plane of the slits at a distance of 1.0 m from it as shown in Fig. 2.42.
If the incident beam makes an angle or `30^(@)` with the x-axis (as in the dotted arrow shown in the figure), find the y-coordinates of the first minima on either side of the central maximum.
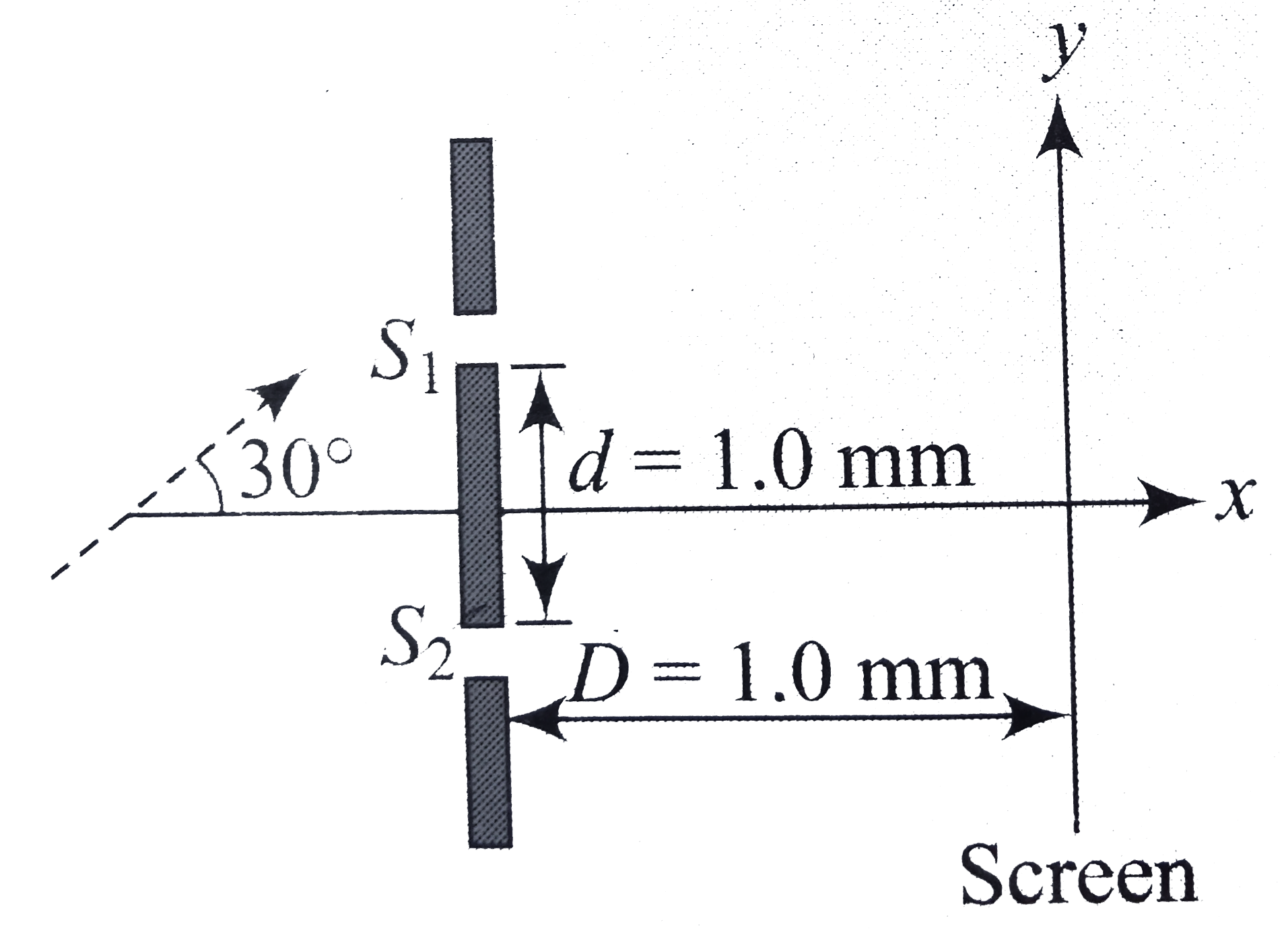
View SolutionA coherent parallel beam of microwaves of wavelength `lambda = 0.5 mm` falls on aYoung's double- slit apparatus. The separation between the slits is 1.0 mm. The intensity of microwaves is measured on a screen placed parallel to the plane of the slits at a distance of 1.0 m from it as shown in Fig. 2.42.
If the incident beam makes an angle or `30^(@)` with the x-axis (as in the dotted arrow shown in the figure), find the y-coordinates of the first minima on either side of the central maximum.
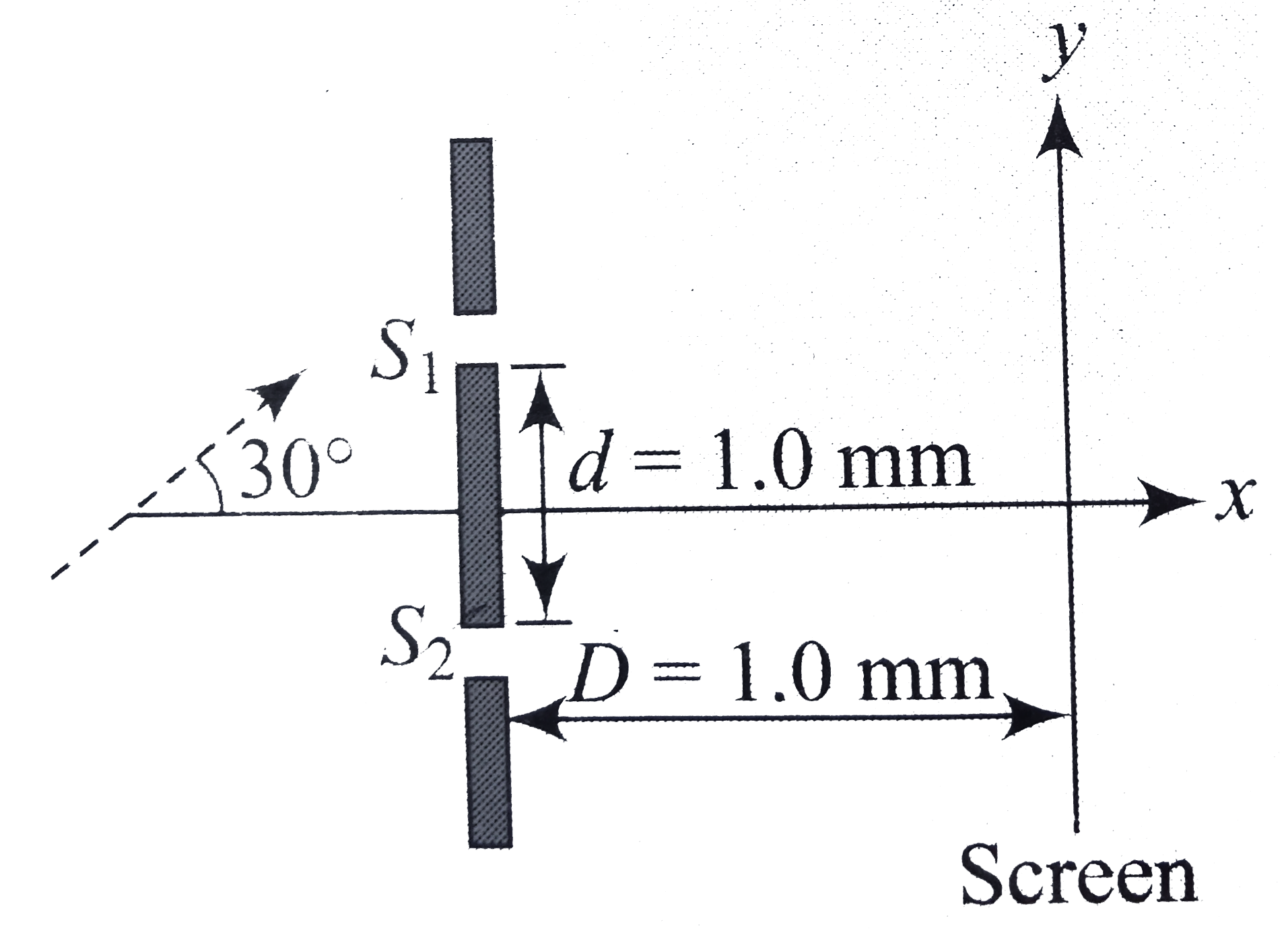
View SolutionA double slit apparatus is immersed in a liquid of refractive index 1.33. it has slit separation of 1 mm and distance between the plane of the slits and the screen is 1.33 m. the slits are illuminated by a parallel beam of light whose wavelength in air is 6300 Å. what is the fringe width?
View SolutionA double-slit apparatus is immersed in a liquid of refractive index 1.33. in It has slit separation of 1 mm and distance between the plane of slits and screen is 1.33 m. The slits are illuminated by a parallel beam or light whose wavelength in air is `6300 Å.`
a. Calculate the fringe width.
b. One of the slits of the apparauts is covered by a thin glass sheet of refractive index 1.53. Find the smallest thickness of the sheet to bring the adjacent minimum on the axix.
View SolutionThree light waves combine at a certain point where thcir electric field components are
`E_(1) = E_(0) sin omega t`,
`E_(2)= E_(0) sin(omega t +60^(@))`,
`E_(3)= E_(0) sin(omega t -30^(@))`.
Find their resultant component E(t) at that point.
View SolutionThe interference pattern is obtained with two coherent light sources of intensity ratio n. In the interference patten, the ratio `(I_(max)-I_(min))/(I_(max)+I_(min))` will be
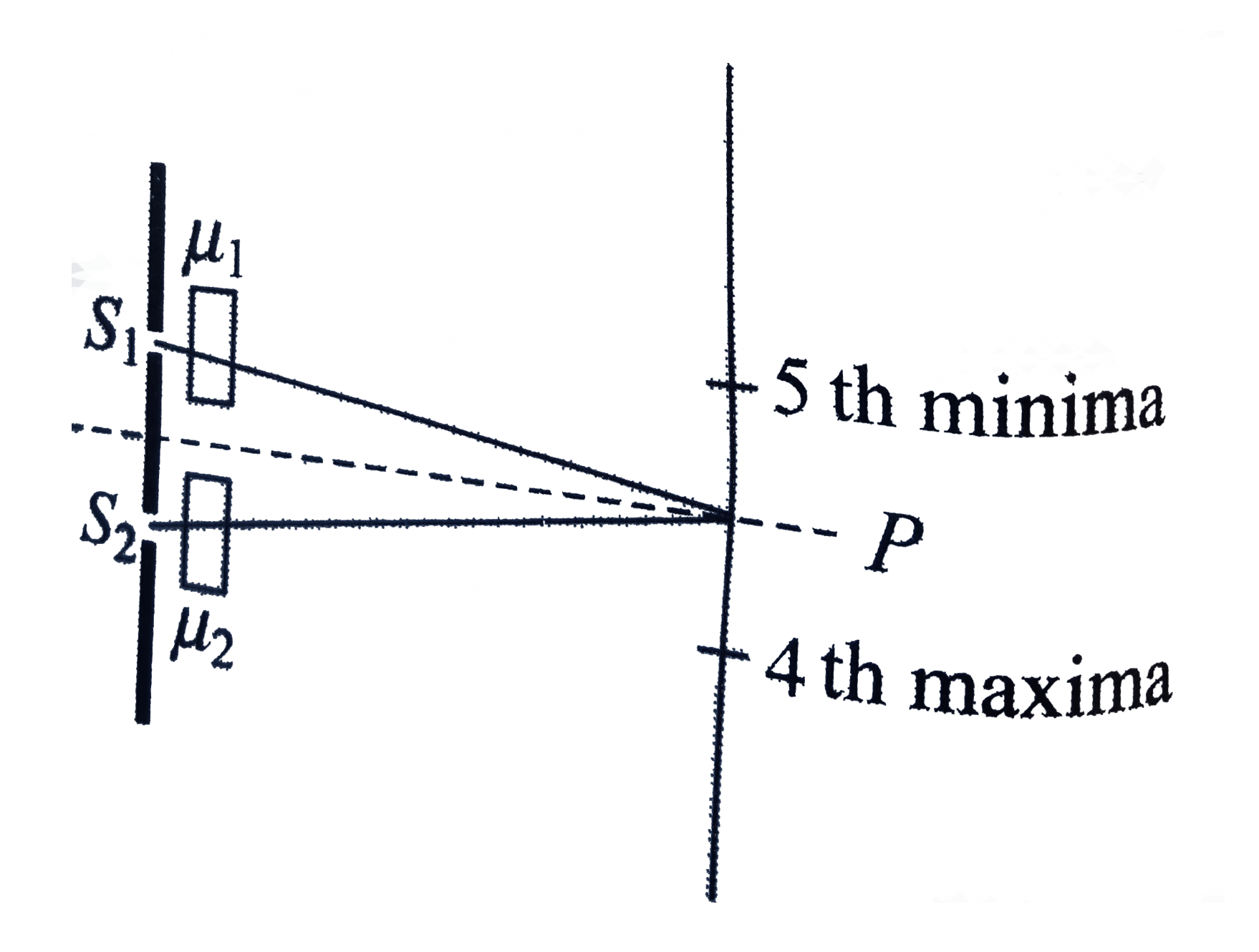
View SolutionIn Young's experiment the upper slit is covered by a thin glass plate of refractive index `1.4` while the lower slit is covered by another glass plate, having the same thickness as the first one but having refractive index `1.7` interference pattern is observed using light of wavelength `5400 Å`
It is found that point P on the screen where the central maximum `(n = 0)` fell before the glass plates were inserted now has `3//4` the original intensity. It is further observed that what used to be the fourth maximum earlier, lies below point P while the fifth minimum lies above P.
Calculate the thickness of glass plate. (Absorption of light by glass plate may be neglected.
 .
.
View SolutionTwo point sources oscillating in the same phase are on a straight line perpendicular to a screen. The nearest source is at a distance of D » `lambda` from the screen. What shape will the interference fringes have on the screen? What is the distance on the screen from the perpendicular to the nearest bright fringe if the distance between the sources is `l=n lambda` (n is an integer)? Note that `lambda` « l.
View SolutionLight from source S is incident on the Fresnel biprism shown in Figure. The light beams refracted by the different faces of the prism partly overlap and produce an interference pattern on a screen on its section AB.
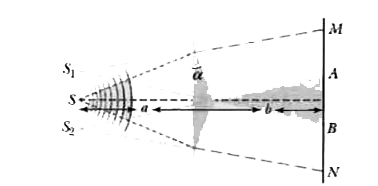
Find the distance between adjacent interference fringes if the distance from the source to the prism is a = 1 m and that from the prism to the screen is b = 4 m. The angle of refraction of the prism is `a = 2 xx 10^(-3)` rad.
The glass of prism has a refractive index of n = 1.5. The wavelength of the light is `lambda=6000 Å`.
View SolutionLight from source S is incident on the Fresnel biprism shown in Figure. The light beams refracted by the different faces of the prism partly overlap and produce an interference pattern on a screen on its section AB.

How many interference fringes can be observed on a screen?
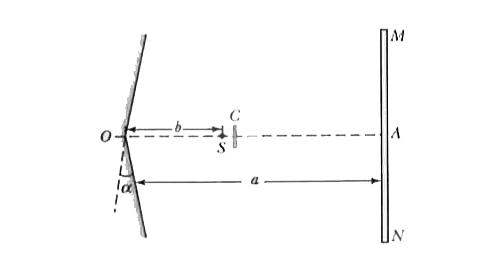
View SolutionTwo flat mirrors form an angle close to `180^(@)`. A source of light S is placed at an equal distance b from the mirrors. Find the distance between adjacent interference fringes on screen MN at a distance `OA = alpha`, from the point of intersection of the mirrors. The wavelength of the light is equal to `lambda`. Shield C does not allow the light to pass directly from the source to the screen.
View SolutionS is a monochromatic point source emitting light of wavelength l = 500 nm. A thin lens of circular shape and of focal length 0.10 m is cut into two identical halves `L_(1)` and `L_(2)` by a plane passing through a diameter. The two halves are placed symmetrically about the central axis SO with a gap of 0.5 mm. The distance along the axis from S to `L_(1)` and `L_(2)` is 0.15 m, while that from `L_(1)` and `L_(2)` to O is 1.30 m. The screen at O is normal to SO. If the third intensity maximum occurs at point A on the screen, find the distance OA.
View SolutionWhite light, with a uniform intensity across the visible wavelength range 430 - 690 nm, is perpendicularly incident on a wate film, of index of refraction `mu = 1.33` and thickness `d = 320`nm, that is suspended in air. At what wavelength `lambda` is the light reflected by the film brightest to an observer?
View SolutionA glass lens is coated on one side with a thin film of magnesium fluoride `(MgF_(2))`to reduce reflection from the lens surface (Fig. 2.26). The Index of refraction of `MgF_(2)` is 1.38, that of the glass is 1.50. What is the least coating thickness that eliminates (via interference) the reflections at the middle of the visible specturm `(lambda = 550nm)`? Assume that the light is approxmately perpendicular to the lens surface.
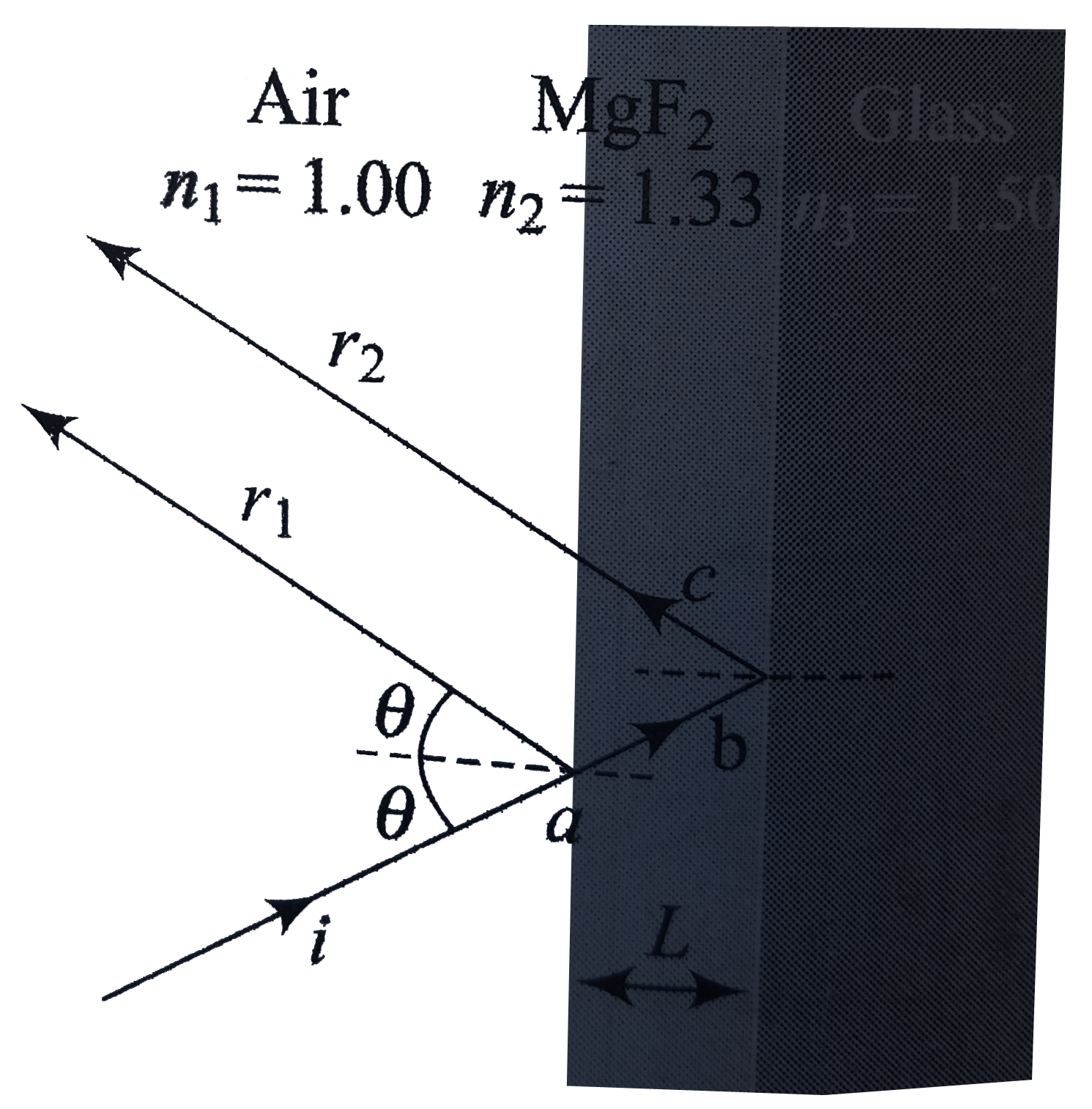
View SolutionA transparent plastic block with a thin wedge of air at the right. (The wedge thickness is exaggerated in the figure.) A broad beam of red light, with wavelength `lambda = 632.8 nm`, is directed downward through the top of the block (at an incidence angle of `0^(@)`). Some of the light that passes into the plastic is reflected back up from the top and bottom surfaces of the wedge, which acts as a thin film (of air) with a thickness that varies uniformly and gradually from `L_(L)` at the left-hand end to `L_(R)` at the righthand end. (The plastic layers above and below the wedge of air are too thick to act as thin films.) An observer looking down on the block sees an interference pattern consisting of six dark fringes and five bright red fringes along the wedge. What is the change in thickness `Delta L (= L_(R)-L_(L))` along the wedge?

View SolutionA slit of width a is illuminated by white light.
(a) For what value of a will the first minimum for red light of wavelength `lambda = 650 nm` appear at `theta= 15^(@)`?
View SolutionA slit of width a is illuminated by white light.
What is the wavelength `lambda` of the light whose first side diffraction maximum is at `15^(@)`, thus coinciding with the first minimum for the red light?
View SolutionFind the intensities of the first three secondary maxima in the single-slit diffraction pattern, measured relative to the intensity of the central maximum
View SolutionA circular converging lens, with diameter d = 32 mm and focal length f = 24 cm, forms images of distant point objects in the focal plane of the lens. The wavelength is `lambda = 550 nm`.
(a) Considering diffraction by the lens, what angular separation must two distant point objects have to satisfy Rayleigh's criterion?
View SolutionA circular converging lens, with diameter d = 32 mm and focal length f = 24 cm, forms images of distant point objects in the focal plane of the lens. The wavelength is `lambda = 550 nm`.
What is the separation Ar of the centers of the images in the focal plane? (That is, what is the separation of the central peaks in the two intensity-versus-position curves?)
View Solution
SAMPLE PROBLEM questions and complete solutions for chapter INTERFERENCE AND DIFFRACTION of RESNICK AND HALLIDAY PHYSICS (HINGLISH) of Class 12