Complete Solutions to Problems For Self Practice of chapter RAY OPTICS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | RAY OPTICS |
| SL ARORA | Problems For Self Practice |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
A 60W lamp is rated at 0.8 watt/candela. Calculate (i) luminous intensity of the lamp, (ii) luminous flux of the lamp, and (iii) illuminance at a distance of 2m from the lamp.
View SolutionIluminance of `2.4 xx 10^(5)lm//m^(2)` of the surface is produced by sunlight falling normally on the surface of the earth. The distance of the earth the sun is `1.5 xx 10^(8)km`. Calculate the luminous intensity and luminous flux of the sun.
View SolutionThe luminous effeciency of a lamp is `51mW^(-1)` and its luminous intensity is 35 cd. Determine the power of the lamp.
View SolutionAt what distance form a light source of 64 cd, will the intensity of illumination because 4 flux ?
View SolutionCalculate the illuminance at a surface distance 0.5m from a ligth source of luminous intensity 200 cd, assuming normal incidence. If the area of the surface be `0.25m^(2)`, what is the luminous flux on this area ?
View SolutionA good photographic print is obtained by an exposure of 2s at a distance of 1m from a 60 candela lamp. What time of exposure must be given to get equally satisfactory results at a distance of 2m from a 200 cadela lamp ?
View SolutionTwo lamps of illuminating powers 25 cd and 100 cd are placed at the end of a photometer bench 2.0 m long. At what point on the bench will the screen of the photometer be equally illuminated on both sides.
View SolutionTwo light sources of intensities 8 cd and 12 cd are placed on the same side of a photometer screen at a distance of 40 cm from it. Where should a 80 cd source be placed to balance the illuminance ?
View SolutionA lamp is hanging at a height of `4 m` above a table. The lamp is lowered by `1 m` . The percentage increase in illuminace will be
View SolutionIn Bunsen's grease spot photometer, light from a lamp with dirty chimney is exactly balanced by that of a candle distant 10 cm from the spot. When the chimney is cleaned, the candle has to be shifted by 2 cm to obtain the balance. Calculate the percentage of light absorbed by dirty chimney.
View SolutionAn electric bulb illuminates a plane surface. The intensity of illumination on the surface at a point 2m away from the bulb is `5 xx 10^(-4)` phot. The line joining the bulb to the point makes an angle of `60^(@)` with the normal to the surface. calculate the intensity of the bulb in candela ? (1 phot `= 1m//cm^(2))`.
View SolutionA lamp is hanging along the axis of a circular table of radius r. at what height should the lamp be placed above the table so that the intensity of illumination at the edge of the table is `(1)/(8)` of that at its centre ?
View SolutionAn electric bulb is hanging above the centre of a circular table of radiys 3m at a height of 3m from the its centre. Find the ratio of illuminance at the centre and at a point on the edge of the table.
View SolutionIn Fig. the circular cross-section of tunnel is shown. A 100 W almp is lighted at the heighest point S. The diameter of the tunnel is 2m. Compare the illuminance at the lowest point P and the point Q of the tunnel.

View SolutionA frosted bulb which may be taken as an isotropic source, gives as illumination of `8lm//m^(2)` at a distance of 5m. Calculate (i) its luminous intensity and (ii) the total luminous flux from the blub.
View SolutionA man is running away from a plane mirror at the speed of `5 ms^(-1)`. With what speed is he receding from his own image ?
View SolutionA plane mirror rotating at an angular velocity of 3 radian/s reflects a light beam. The angular velocity of the reflected beam is -
View SolutionA ray of light is incident at an angle of `60^(@)` on a horizontal plane mirror. Through what angle should the mirror be tilted to make the reflected ray horizontal ?
View Solutionrays of light strike a horizontal plane mirror at an angle of `45^(@)`. At what angle should be a second plane mirror be placed in order that the reflected ray finally be reflected horizontally from the second mirror.
View SolutionTwo plane mirrors are inclined at angle `theta` as shown in figure. If a ray parallel to OB strikes the other mirror at P and finally emerges parallel to OA after two reflections then `theta` is equal to
View SolutionAn object 0.04 m high is placed at a distance of 0.8 m from a concave mirror of radius of curvature 0.4 m. find the position, nature and the size of the image formed.
View SolutionFind the size, nature and position of image formed by a concave mirror, when an object of size 1 cm is placed at a distance of 15 cm. Given focal length of mirror is 10 cm.
View SolutionAn object is placed in front of a concave mirror of radius of curvature `40 cm` at a distance of `10 cm`. Find the position, nature and magnification of the image.
View SolutionAn object is placed at a distance of 15 cm from a convex mirror and images is formed at a distance of 5 cm from the mirror. Calculate the radius of curvature of the mirror.
View SolutionA convex mirror and a concave mirror of radius 10cm each are placed 15cm apart facing each other. An object is placed midway between them. If the reflection first takes place in the concave mirror and then in convex mirror, the position of the final image is
View SolutionA candle flame 2 cm high is palced at distance of 2 metere from a wall. How far from the wall must a concave mirror to placed in order to form an images of the flame 6 cm high on the wall ?
View SolutionA dentist concave mirror has a radius of curvature of `30 cm`. How far must it be placed from a small cavity in order to get a virtual image magnified `5` times ?
View SolutionFind the position of an object which when placed in front of a concave mirror of focal length 20 cm, produces a virtual image which is twice the size of the object.
View SolutionA concave mirror forms a real image four times as tall as the object placed 10 cm infront of mirror. Find the position of the image and the radius of curvature of the mirror.
View SolutionWhen an object is placed at a distance of `60 cm` from a convex spherical mirror, the magnification produced is `1//2`. Where should the object be placed to get a magnification of `1//3` ?
View SolutionA convex mirror produces a magnification of `1//2` when the object is placed at a position A and a magnification of `1//3` when the object is at a position B. If the separation between the positions A and B be 30 cm, what is the focal length of the mirror ?
View SolutionAn object of `1cm^(2)` face area is placed at a distance of 1.5m from a screen. How far from the object should a concave mirror be placed so that it forms `4 cm^(2)` image of object on the screen? Also, calculate the focal length of the mirror.
View SolutionA rectangular tank 8m deep is full of water. By how much does the bottom appear to be raised if the refractive index of water is `4//3`?
View SolutionA travelling microscope is focussed on a mark made on a paper. When a slab of `1.45cm` thickness is placed on the marl, the microscope has to be raised through 0.49 cm to focus the mark again. Calculate the refractive index of glass.
View SolutionA printed page is kept pressed by a glass cube `(mu = 1.6)` of edge 6.0cm. By what amount will the printed letters appear to be shifted when viewed from the top ?
View SolutionThe velocity of light in glass is `2 xx 10^(8)ms^(-1)` while that in vaccum is `3 xx 10^(8)ms^(-1)`. By how much would an ink dot appeat to be raised when covered by a glass plate of 4.5 cm thickness.
View SolutionCalculate the index of refraction of a liquid from the following into glass:
(a) Reading for the bottom of an empty beaker: 11.324 cm
(b) Reading for the bottom of the beaker, when partially filled with the liquid: 11.802 cm
(c) Reading for the upper level of the liquid in the beaker: 12.895cm
View SolutionWhile determining the refractive index of a liquid experimentally, the microscope was focussed at the bottom of a beaker, when its reading was 3.965 cm. on pouring liquid upto a height 2.537 cm inside the beaker, the reading of the refocussed microscope was 3.348 cm. Find the refractive index of the liquid.
View SolutionA vessel contains water up to a height of 20 cm and above it an oil up to another 20 cm. The refractive indices of the water and the oil are 1.33 and F30 respectively. Find the apparent depth of the vessel when viewed from above.
View SolutionIn Fig. a plane mirror lies at a height h above the bottom of a beaker containingwater (refractive index `mu`) upto a height f. Find the position of the image of the
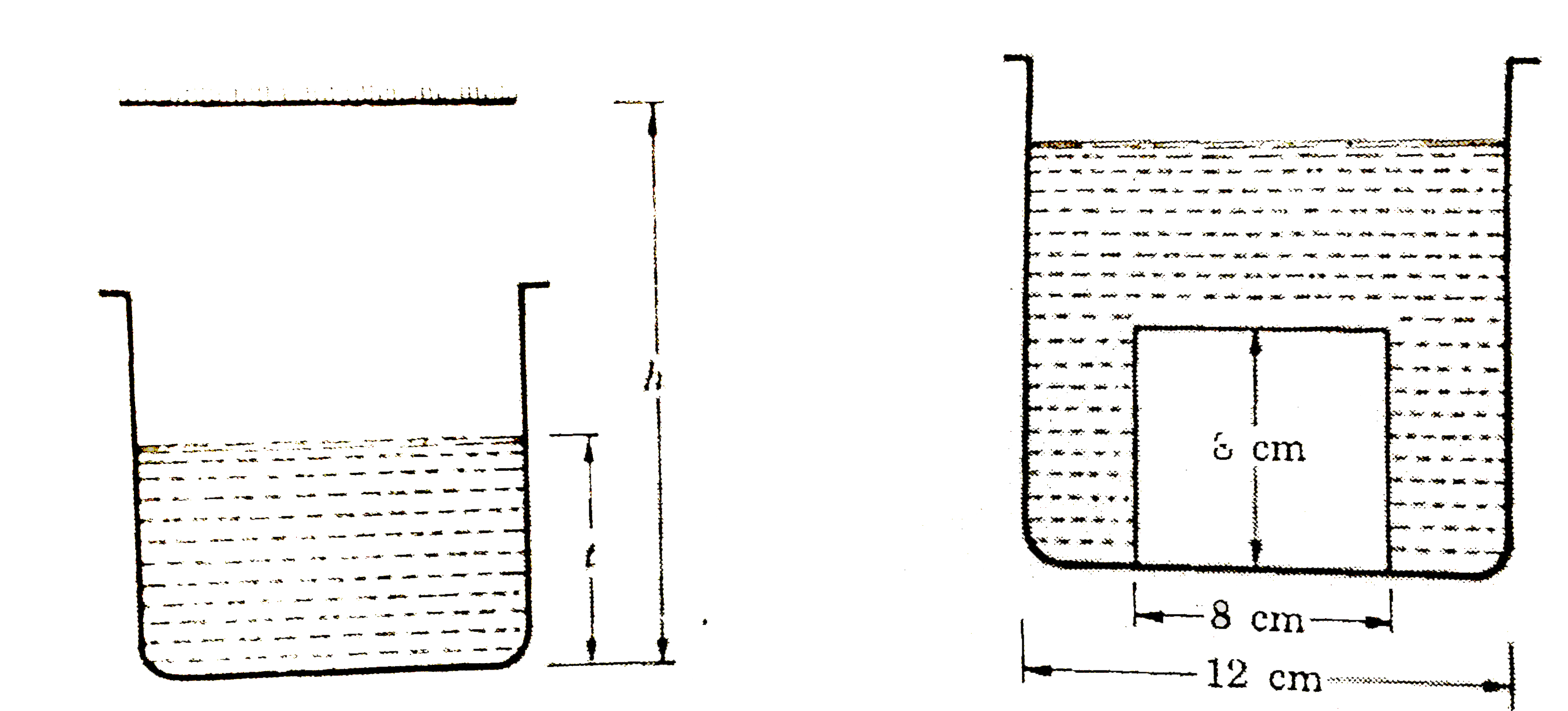
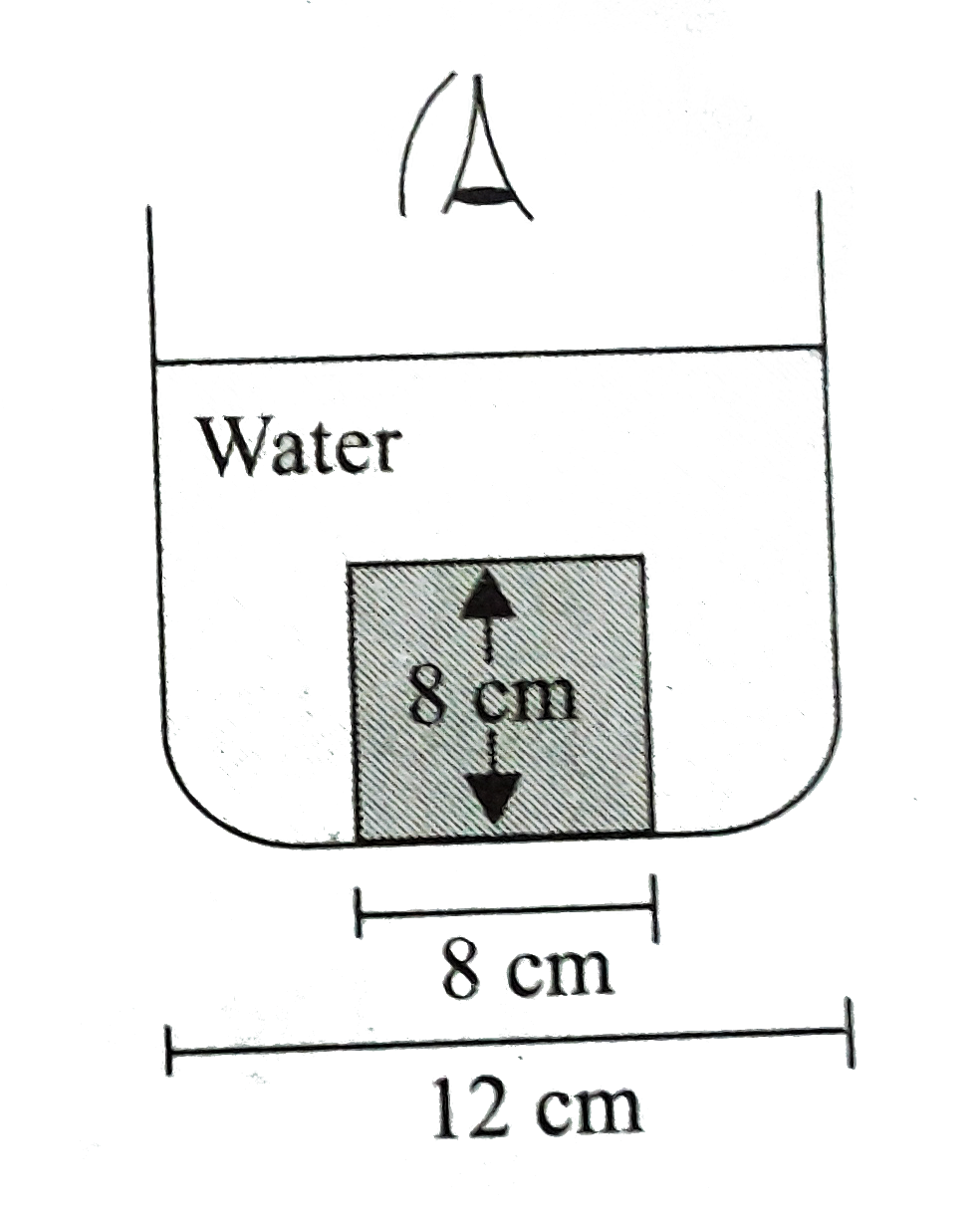
View SolutionA cylindrical vessel of diameter 12 cm contains `800picm^(3)` of water. A cylindrical glass piece of diameter `8.0cm` and height ``8.0 cm is placed in the vessel. If the bottom of the vessel under the glass piece is seen by the paraxial rays, locate its image. The index of refraction of glass is 1.50 and that of water is 1.33.
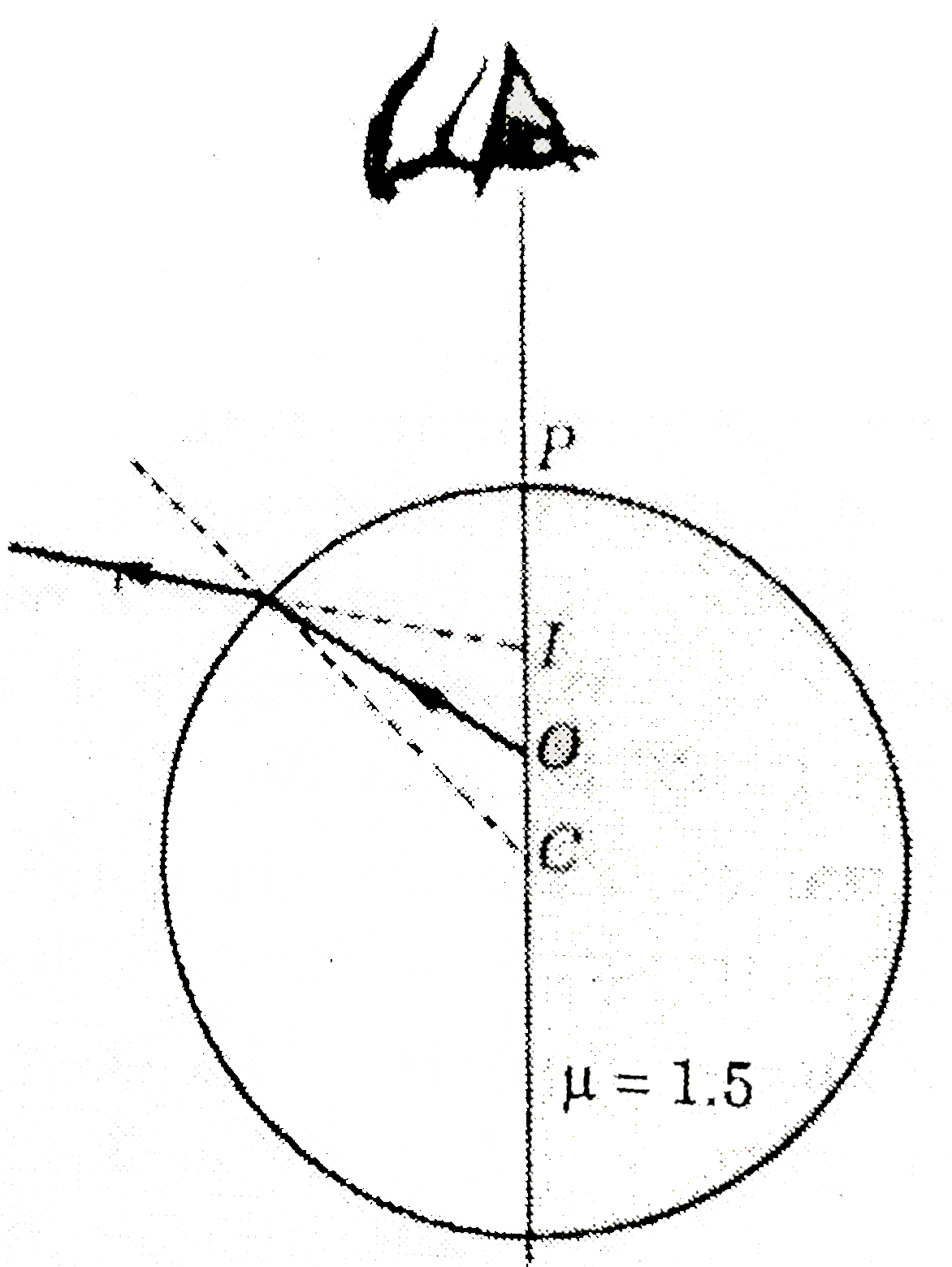
View SolutionIf critical angle for a material to air is `30^(@)`, the refractive index of the material will be
View SolutionAn optical fibre (mu = 1.72) is surrounded by a glass coating (mu= 1.50). Find the critical angle for total internal reflection at the fibre-glass interface.
View SolutionWhat is the small index of refractive of the material of a right angled prism with equal sides for which a ray of light entering one of the sides normally will be totally reflected ?
View SolutionFind the maximum angle of refraction when a light ray is refracted from glass `(mu= 1.50)` to air.
View SolutionA luminous object O is located at the bottom of a big pool of liquid of refractive index `mu` and depth h. The object O emits rays upwards in all directions, so that a circle of light is formed at the surface of the liquid by the rays which are refracted into the air. what happens to the rays beyond the circle ? Determine the radius and the area of the circle .
View SolutionOne end of a cylindrical rod is grounded to a hemispherical surface of radius`R=20mm`.It is immersed in water`(mu=4//3)`.If the refractive index of the rod is`1.5`and an object is placed in water on the axis at a distance of`10cm`form the pole ,then the position of the image is ................(determine)
View SolutionA spherical convex surface separates object and image space of refractive index `1.0 and 4/3.` If radius of curvature of the surface is `10cm,` find its power.
View SolutionA mark placed on the surface of a sphere is viewed through glass from a position directly opposite. If the diameter of the sphere is `10 cm` and refractive index of glass is `1.5`, find the position of the image.
View SolutionA glass sphere of radius 15 cm has a small bubble 6 cm from its centre. The bubble is viewed along a diameter of the sphere from the side on which it lies. How for from the surface will it appear to be if the refractive index of glass is 1.5 ?
View SolutionAn object is placed `50 cm` from the surface of a glass sphere of radius `10 cm` along the diameter. Where will the final image be formed after refraction at both the surfaces ? `mu` of glass `=1.5`.
View SolutionA small object is 2 cm below the concave meniscus of water in a test tube . The radius of the meniscus is 5mm and `mu` for water is `4//3`. Find the nature and position of the image.
View SolutionA spherical surface of radius 30 cm separates two transparent media A and B with refractive indices 1'33 and 1.48 respectively. The medium A is on the convex side of the surface. Where should a point object be placed in medium A so that the paraxial rays become parallel after refraction at the surface ?
View SolutionFig shows a small air bubble inside a glass sphere `(mu = 1.5)` of radius 10 cm. the bubble is 4.0 cm below the surface and is viewed normally from the outside. Find the apparent depth of the bubble.
View SolutionA double convex lens has radii 20 cm. The index of refraction of glass is 1.5. Compute the focal length of this lens in air and when immersed in carbon disulphide of refractive index 1.63.
View SolutionThe focal length of a double convex lens is equal to radius of curvature of either surface. The refractive index of its material is
View SolutionFig. 6(b).54. shows a thin lens with centres of curvature `C_(1) and C_(2)`. If `mu = 1.5`, what is its focal length ?
View SolutionA plano-convex lens `(mu = 1.5)` has a curved surface of radiys 15 cm. what is its focal length ?
View SolutionThe focal length of a concave-convex lens of radii of curvature 5 cm and 10 cm is 20 cm. what will be its focal length in water ? Given `.^(a)mu_(w) = 4//3`.
View SolutionA convex lens of refractive index 1.5 is immersed in a liquid of refractive index (i) 1.6 (ii) 1.3 and (iii) 1.5. what changes happens to the focal length of the lens in the three cases ?
View SolutionThe two surfaces of a double concave lens are of curvature 10 cm and 40 cm. Find the focal length of the lens in water. The refractive index of water is `4//3` and that of the lens of the material is 3/2.
View SolutionThe focal length of a plano-convex lens is 20 cm in air. Refractive index of glass is 1.5. Calculate (i) the radius of curvature of lens surface and (ii) its focal length when immersed in liquid of refractive index 1.6
View SolutionThe focal length of a convex lens of glass `(mu = 1.5)` in air is 30 cm. Find its focal length when the lens is placed in water `(mu = 4//3)`.
View SolutionA lens of refractive index `mu` becomes a lens of focal length f' when immersed in a liquid of refractive index `mu`'. If the focal length of the lens in air is f, prove that
`f' = f.(mu'(mu-1))/((mu-mu'))`.
View SolutionThe radii of curvature of each surface of a convex lens is `20 cm` and the refractive index of the material of the lens is `3//2` (i) Calculate its focal length (ii) If this is cut along the plane `AB`. What will be formed ? (iii) What happens if the lens is cut along `CD` ?
View SolutionThe radii of curvatureof double convex lens of glass `(mu = 1.5)` are in the ratio of `1 : 2`. This lens renders the rays parallel coming from an illuminated filament at a distance of `6 cm`. Calculate the radii of curvature of its surfaces.
View SolutionWhere should an object be placed from a converging lens of focal length 10 c, so as to obtain a virtual image of magnification 2 ?
View SolutionAt what distance should an object be placed from a convex lens of focal langth `15 cm` to obtain an image three times the size of the object ?
View SolutionA convex lens is placed on an optical bench and is moved till it gives a real image of an object at a minimum distance of 80 cm from the latter. Find the focal length of the lens. If the object is placed at a distance of 15 cm from the lens, find the position of the image.
View SolutionA convex lens of focal length 30 cm is placed between a screen and a square plate of area `4cm^(2)`. The image of the plate formed on the screen is `16cm^(2)`. Calculate the distance between the plate and the screen.
View SolutionAn object is 60 cm in front of a thin lens, the image being 300 cm on the other side of the lens. Calculate the displacement of the image, when the object is moves 20 cm nearer to the lens.
View SolutionA source of light and a screen are placed 90 cm apart. Where should a convex lens of 20 cm focal length be placed in order to form a real image of the source on the screen ?
View SolutionAn object is placed at a distance of `1.5 m` from a screen and a convex lens is interposed between them. The magnification produced is `4`. What is the focal length of the lens ?
View SolutionThe distance between a convex lens and a plane mirror is 15 cm. The parallel rays incident on the convex lens, after reflection from the mirror, form image at the optical centre of the lens. Draw the ray-diagram and find out the focal length of the lens.
View SolutionA concave lens focal length 10 cm is placed on the axis of concave mirror of 10 cm radius at a distance of 5 cm from the mirror. An object is placed so that the light coming from it first passes through the lens, the gets reflected from the mirror, again passes through the lens to form an inverted image coincident with the object itself. Determine the position of the object.
View SolutionA concave lens is placed in the path of convergent rays. The rays are focussed on the axis 15 cm behind the lens. Where would these rays have been focussed in the absence of the lens ? Focal length of the lens is 30 cm.
View SolutionA needle 10 cm long is placed along the axis of a convex lens of focal length 10 cm such that the middle point of the neddle is at a distance of 10 cm from the lens. Find the length of the image of the neddle.
View SolutionWhen a slide is placed 15 cm behind the lens in a projector, an image is formed at 3 infront of the lens. (i) Show the image formation by a ray diagram. (ii) Find the focal length of the lens. (iii) What will be the distance between the lens and the slide in order to get and image at a distance 4 metre from the lens ? (iv) Determine the magnification for the case (iii).
View SolutionIn the diagram shows below rays are coming from infinity and after passing through both the lenses meet on a screen placed at a distance of 30 cm from the concave lens. Calculate the focal length of the concave lens.

View SolutionIn the following ray diagram are given the position of an object O, image I and two lenses `L_(1)` and `L_(2)`. The focal length of `L_(1)` is also given. Find the focal length of `L_(2)`.

View SolutionIn the following diagram are shown the position of an object O, image I and two lenses. The focal length of one lens is also given. Determine the focal length of the other lens.
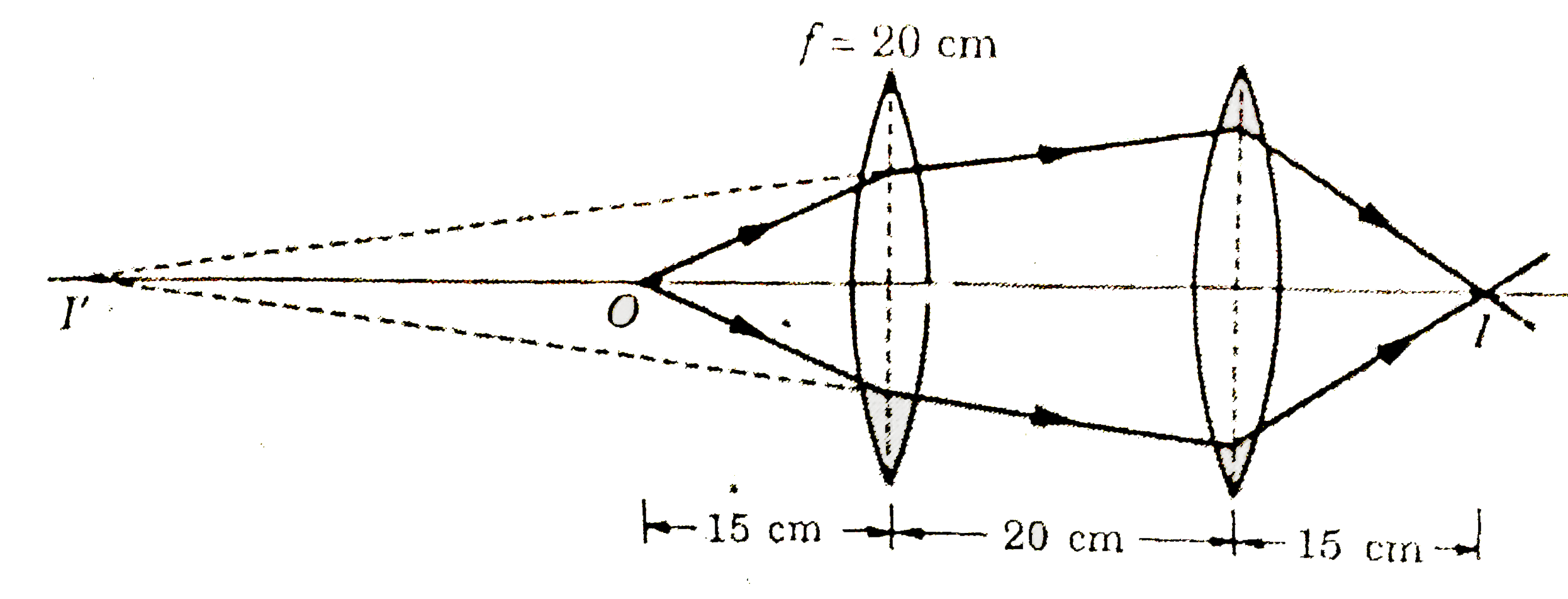
View SolutionA compound lens has been formed by joinined a convex and a concave lens, each of focal length 30 cm. what is the focal length of the combination? What will be the power ?
View SolutionTwo thin lenses of power `+ 3 D and - 1 D` are held contact with each other. Focal length of the combination is :
View SolutionA what distance must an object be placed from convex lens of power 4D to obtain a real image three times the size of the object ?
View SolutionFind the focal length and power of a convex lens, which when placed in contact with a concave lens of focal length `25 cm` forms a real image `5` times the size of the object placed `20 cm` from the combination.
View SolutionThe power of a thin convex lens of glass is `5 dioptre`. When it is immersed in a liquid of refractive index `mu`, it behave like a diverging lens of focal length `1m`. Calculate `mu` of liquid, if `mu` of glass `= 3//2`.
View SolutionA concave lens is kept in contact with a convex lens of focal length `20 cm`. The combination works as a converging lens of focal length `100 cm`. Calculate power of concave lens.
View SolutionA compound lens is made of two lenses having powers `+15.5 D` and `-5.5D`. An object of 3cm height is placed at a distance of 30 cm from this compound lens. Find the size of the image.
View SolutionRay coming from an object situated at infinity, fall on a convex lens and an image is formed at a distance of 16 cm from the lens. When a concave lens is kept in contact with the convex lens, the image is formed at a distance of 20 cm from the lens combination. Calculate the focal length of the concave lens.
View SolutionA ray of light is incident at an angle of `60^(@)` on one face of a prism of angle `30^(@)`. The ray emerging out of the prism makes an angle of `30^(@)` with the incident ray. The emergent ray is
View SolutionThe refracting angle of a glass prism is `60^(@)`. The value of minium deviation for light passing through the prism is `40^(@)`. Calculate the value of refractive index of the material of the prism. Given `sin 50^(@) = 0.766`.
View SolutionThe refractive index of the material of a prism of `60^(@)` angle for yellow light is `sqrt(2)`. Calculate angle of minimum deviation, angle of incidence and angle of refraction.
View SolutionA ray of light incident at `49^(@)` on the face of an equilateral prism passes symmetrically. Calculate the refractive index of the material of the prism.
View SolutionA glass prism has a refracting angle of `60^@`. The angle of minimum deviation is `40^@`. If velocity of light in vacuum is `3 xx 10^8 m//s`. Calculate the velocity of light in glass. What is the angle of incidence ?
View SolutionA ray incident normally on one face of a right-angled isosceles glass prism in air is deviated through `90^(@)`. What can you say about the refractive index of glass ?
View SolutionAs shown in Fig. `PQ` is a ray incident on prism `ABC`. Show the corresponding refracted and emergent rays. The critical angle for the material of the prism is `45^@`. What is refractive index of the material of prism ?
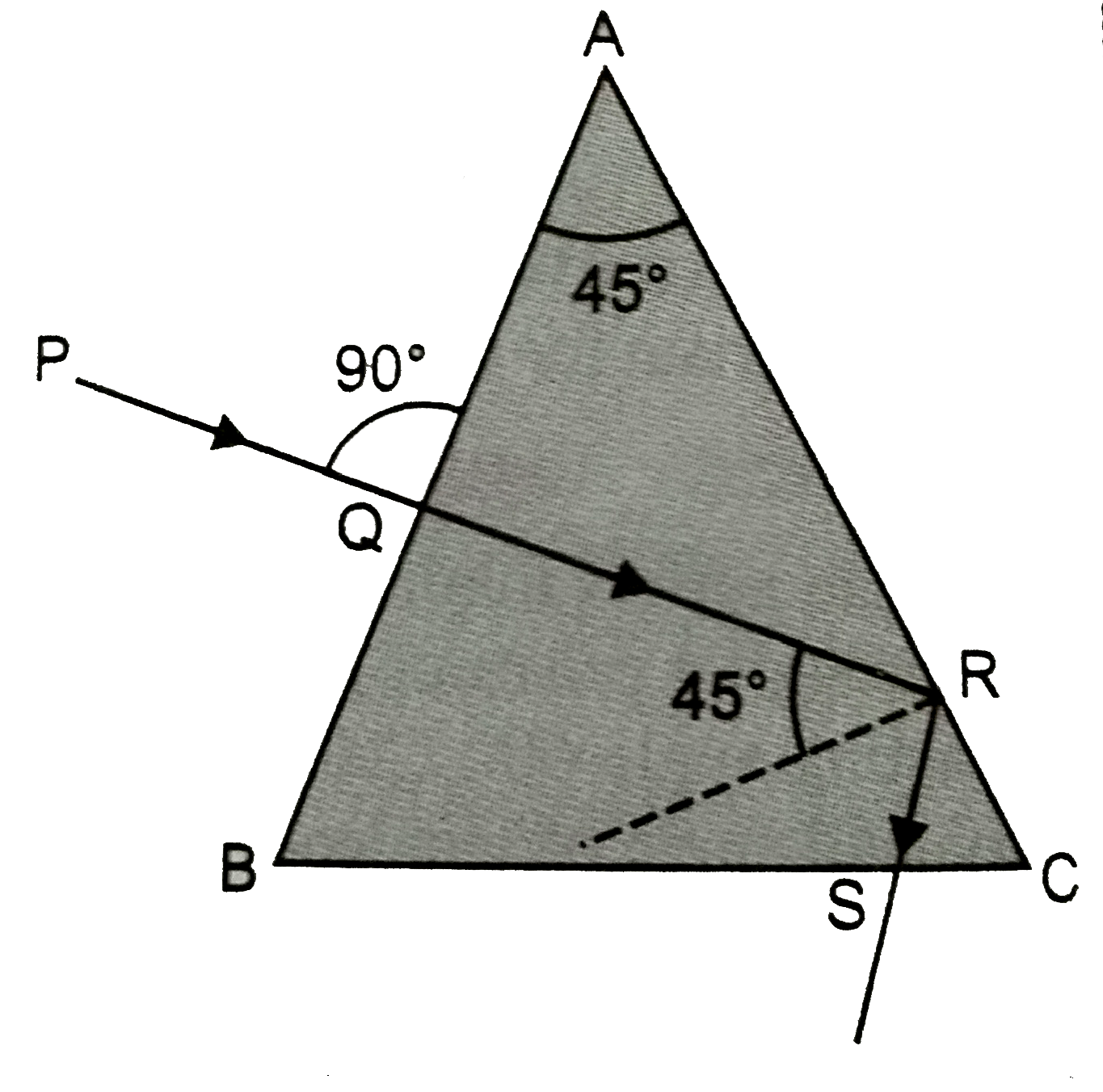 .
.
View SolutionShow that a light ray will pass through an equilateral glass prism `(mu = 1.5)`. If the angle of incidence is greater than `30^(@)`.
View SolutionA ray of light falls on a normally on a refracting face of a prism. Find the angle of prism if the ray just fails to emerge from the prism `(mu=3//2).`
View SolutionA ray of light is incident on the glass prism at an angle of `40^(@)`. Find the angle of emergence, if the angle of prism is `60^(@)` and refractive index is 1.5.
View SolutionA ray of light falls on a glass prism at a angle of incidence of `30^(@)`. Find the direction of the emergent ray if the angle of the prism is `60^(@)` and refractive index is 1.50
View Solution
Problems For Self Practice questions and complete solutions for chapter RAY OPTICS of DHANPAT RAI & CO PHYSICS (HINGLISH) of Class 12