Complete Solutions to EXERCISES of chapter MENSURATION of Class 8 book with complete answers and questions
| Class 8 | MATHS |
| Chapter | MENSURATION |
| NCERT EXEMPLAR | EXERCISES |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
A cube of side 5 cm is painted on all its faces. If it is sliced into 1 cubic centimetre cubes, how many 1 cubic centimetre cubes will have exactly one of their faces painted?
View SolutionA cube of side 4 cm is cut into 1 cm cubes. What is the ratio of the surface areas of the original cubes and cut-out cubes?
View SolutionA circle of maximum possible size is cut from a square sheet of board. Subsequently, a square of maximum possible size is cut from the resultant circle. What will be the area of the final square?
View SolutionWhat is the area of the largest triangle that can be fitted into a rectangle of length l units and width w units?
View SolutionIf the height of a cylinder becomes `1/4` of the original height and the radius is doubled, then which of the following will be true?
View SolutionIf the height of a cylinder becomes `1/4` of the original height and the radius is doubled, then which of the following will be true?
View SolutionIf the height of a cylinder becomes `1/4` of the original height and the radius is doubled, then which of the following will be true?
View SolutionThe surface area of the three coterminus faces of a cuboid are 6, 15 and 10 `cm^(2)` respectively. The volume of the cuboid is
View SolutionIf a regular hexagon is inscribed in a circle of radius r, then find the perimeter of the hexagon.
View SolutionThe dimensions of a godown are 40 m, 25 m and 10 m. If it is filled with cuboidal boxes each of dimensions `2 m xx 1.25 m xx 1 m`, then the number of boxes will be
View SolutionThe volume of a cube is 64 `cm^3`. Its surface area is
View SolutionIf the radius of a cylinder is tripled but its curved surface area is unchanged, then its height will be
View SolutionHow many small cubes with edge of 20 cm each can be just accommodated in a cubical box of 2 m edge?
View SolutionThe volume of a cylinder whose radius r is equal to its height is
View SolutionThe volume of a cube whose edge is 3x is
View SolutionThe figure ABCD is a quadrilateral in which AB = CD and BC = AD. Its area is
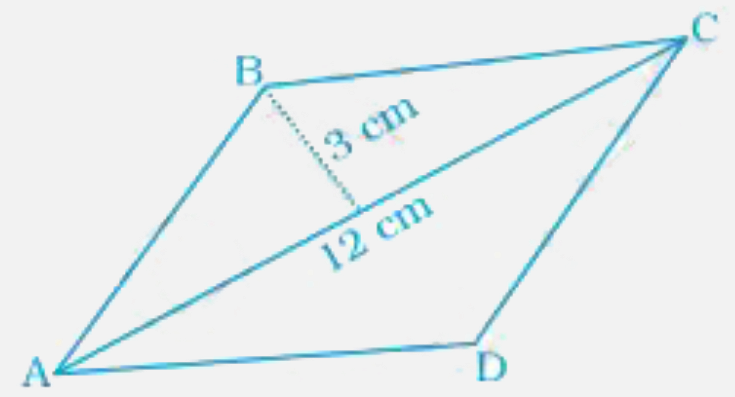
View SolutionWhat is the area of the rhombus ABCD below if AC = 6 cm, and BE = 4cm?
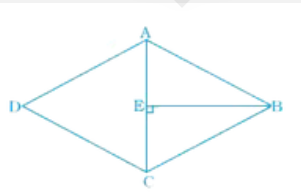
View SolutionThe area of a parallelogram is 60 `cm^2` and one of its altitude is 5 cm. The length of its corresponding side is
View SolutionIf the perimeter of a trapezium be `52cm`, its non parallel sides are equal to `10cm` each and its altitude is `8cm,` find the area of the trapezium.
View SolutionArea of a quadrilateral ABCD is 20 `cm^2` and perpendiculars on BD from opposite vertices are 1 cm and 1.5 cm. The length of BD is
View SolutionA metal sheet 27 cm long, 8 cm broad and 1 cm thick is melted into a cube. The side of the cube is
View SolutionThree cubes of metal whose edges are 6 cm, 8 cm and 10 cm respectively are melted to form a single cube. The edge of the new cube is
View SolutionA covered wooden box has the inner measures as 115 cm, 75 cm and 35 cm and thickness of wood as 2.5 cm. The volume of the wood is
View SolutionThe ratio of radii of two cylinders is 1: 2 and heights are in the ratio 2:3. The ratio of their volumes is
View SolutionTwo cubes have volumes in the ratio 1:64. The ratio of the area of a face of first cube to that of the other is
View SolutionThe surface areas of the six faces of a rectangular solid are 16, 16, 32, 32, 72 and 72 square centimetres. The volume of the solid, in cubic centimetres, is
View SolutionRamesh has three containers.
(a) Cylindrical container A having radius r and height h,
(b) Cylindrical container B having radius 2r and height 1/2 h, and
(c) Cuboidal container C having dimensions `r xx r xx h`
The arrangement of the containers in the increasing order of their volumes is
View SolutionIf R is the radius of the base of the hat, then the total outer surface area of the hat is

View SolutionA cube of side 4 cm is painted on all its sides. If it is sliced in 1 cubic cm cubes, then number of such cubes that will have exactly two of their faces painted is __________.
View SolutionA cube of side 5 cm is cut into 1 cm cubes. The percentage increase in volume after such cutting is __________.
View SolutionThe surface area of a cuboid formed by joining two cubes of side a cm face to face is __________.
View SolutionIf the diagonals of a rhombus get doubled, then the area of the rhombus becomes __________ its original area.
View SolutionIf a cube fits exactly in a cylinder with height h, then the volume of the cube is __________ and surface area of the cube is __________.
View SolutionThe volume of a cylinder becomes __________ the original volume if its radius becomes half of the original radius.
View SolutionThe curved surface area of a cylinder is reduced by ____________ per cent if the height is half of the original height.
View SolutionThe volume of a cylinder which exactly fits in a cube of side a is __________.
View SolutionThe surface area of a cylinder which exactly fits in a cube of side b is __________.
View SolutionIf the diagonal d of a quadrilateral is doubled and the heights `h_1` and `h_2` falling on d are halved, then the area of quadrilateral is __________.
View SolutionThe perimeter of a rectangle becomes __________ times its original perimeter, if its length and breadth are doubled.
View SolutionA trapezium with 3 equal sides and one side double the equal side can be divided into __________ equilateral triangles of _______ area.
View SolutionAll six faces of a cuboid are __________ in shape and of ______ area.
View SolutionOpposite faces of a cuboid are _________ in area.
View SolutionCurved surface area of a cylinder of radius h and height r is _______.
View SolutionTotal surface area of a cylinder of radius h and height r is _________
View SolutionVolume of a cylinder with radius h and height r is __________.
View SolutionArea of a rhombus `=1/2` product of ____________.
View SolutionTwo cylinders A and B are formed by folding a rectangular sheet of dimensions 20 cm `xx` 10 cm along its length and also along its breadth respectively. Then volume of A is ________ of volume of B.
View SolutionTwo cylinders A and B are formed by folding a rectangular sheet of dimensions 20 cm × 10 cm along its length and also along its breadth respectively. Curved surface area of A is ________ curved surface area of B.
View Solution__________ of a solid is the measurement of the space occupied by it.
View Solution__________ surface area of room = area of 4 walls.
View SolutionTwo cylinders of equal volume have heights in the ratio 1:9. The ratio of their radii is __________.
View SolutionTwo cylinders of same volume have their radii in the ratio 1:6, then ratio of their heights is __________.
View SolutionState whether the statements are true (T) or false (F).
The areas of any two faces of a cube are equal.
View SolutionState whether the statements are true (T) or false (F).
The areas of any two faces of a cuboid are equal.
View SolutionState whether the statements are true (T) or false (F).
The surface area of a cuboid formed by joining face to face 3 cubes of side x is 3 times the surface area of a cube of side x.
View SolutionState whether the statements are true (T) or false (F).
Two cuboids with equal volumes will always have equal surface areas.
View SolutionState whether the statements are true (T) or false (F).
The area of a trapezium become 4 times if its height gets doubled.
View SolutionState whether the statements are true (T) or false (F).
A cube of side 3 cm painted on all its faces, when sliced into 1 cubic centimetre cubes, will have exactly 1 cube with none of its faces painted.
View SolutionState whether the statements are true (T) or false (F).
Two cylinders with equal volume will always have equal surface areas.
View SolutionState whether the statements are true (T) or false (F).
The surface area of a cube formed by cutting a cuboid of dimensions `2 *1 * 1` in 2 equal parts is 2 sq. units.
View SolutionState whether the statements are true (T) or false (F).
Ratio of area of a circle to the area of a square whose side equals radius of circle is `1 : pi.`
View SolutionThe area of a rectangular field is 48 `m^2` and one of its sides is 6m. How long will a lady take to cross the field diagonally at the rate of 20 m/minute?
View SolutionThe circumference of the front wheel of a cart is 3 m long and that of the back wheel is 4 m long. What is the distance travelled by the cart, when the front wheel makes five more revolutions than the rear wheel?
View SolutionFour horses are tethered with equal ropes at 4 corners of a square field of side 70 metres so that they just can reach one another. Find the area left ungrazed by the horses.
View SolutionThe walls and ceiling of a room are to be plastered. The length, breadth and height of the room are 4.5m, 3m and 350cm, respectively. Find the cost of plastering at the rate of Rs. 8 per square metre.
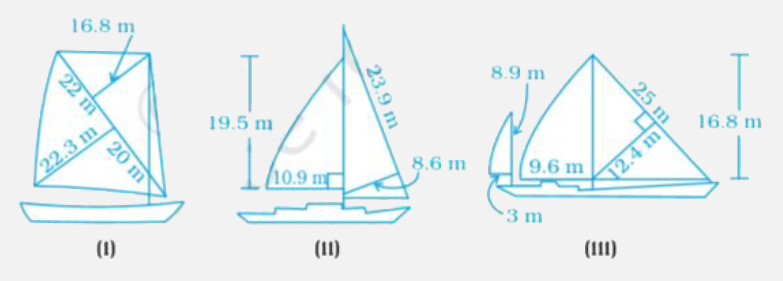
View SolutionMost of the sailboats have two sails, the jib and the mainsail. Assume that the sails are triangles. Find the total area of each sail of the sail boats to the nearest tenth.
View SolutionThe area of a trapezium with equal non-parallel sides is 168 `m^2`. If the lengths of the parallel sides are 36 m and 20 m, find the length of the non-parallel sides.
View SolutionMukesh walks around a circular track of radius 14 m with a speed of 4 km/hr. If he takes 20 rounds of the track, for how long does he walk?
View SolutionThe areas of two circles are in the ratio 49:64. Find the ratio of their circumferences.
View SolutionThere is a circular pond and foot-path runs along its boundary. A man walks around it, exactly once, keeping close to the edge. If his step is 66 cm long and he takes exactly 400 steps to go around the pond, what is the diameter of the pond?
View SolutionA running track has 2 semicircular ends of radius 63 m and two straight lengths. The perimeter of the track is 1000 m. Find each straight length.
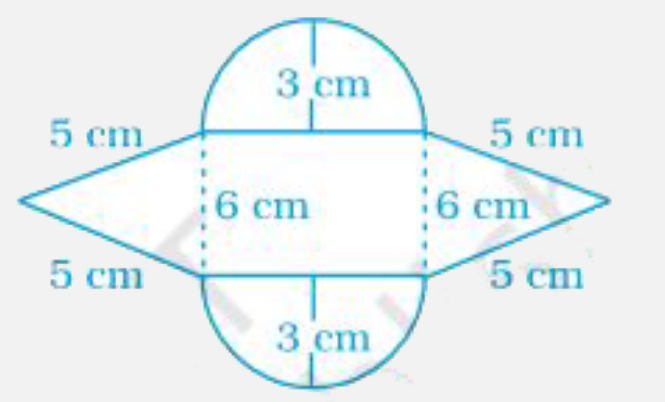
View SolutionFind the perimeter of the given figure.
View SolutionA bicycle wheel makes 500 revolutions in moving 1 km. Find the diameter of the wheel.
View SolutionA boy is cycling such that the wheels of the cycle are making 140 revolutions per minute. If the diameter of the wheel is 60 cm, calculate the speed per hour with which the boy is cycling.
View SolutionFind the length of the largest pole that can be placed in a room of dimensions `12 m xx 4 m xx 3 m`.

View SolutionFind the area of the following fields. All dimensions are in metres.
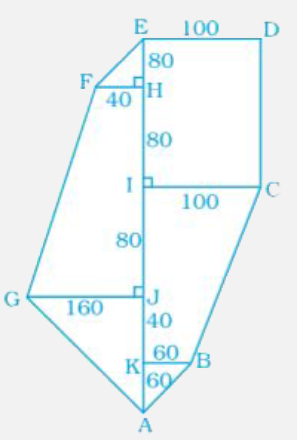
View SolutionFind the area of the following fields. All dimensions are in metres.
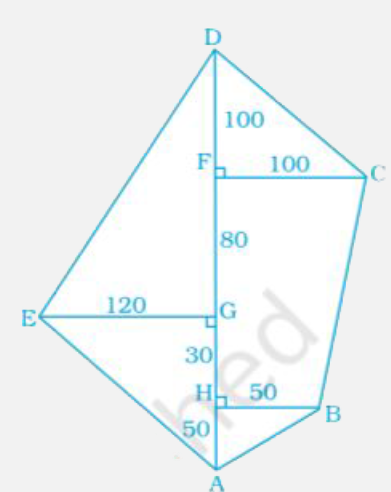
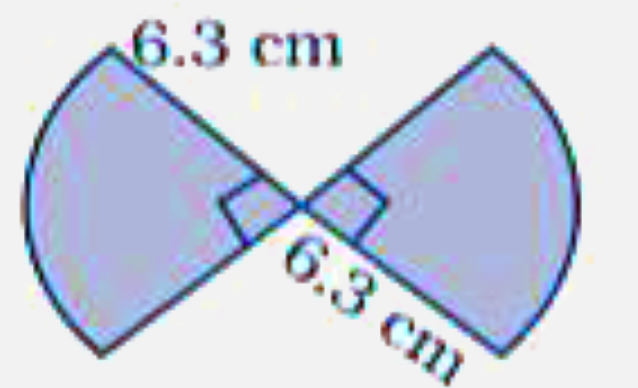
View SolutionFind the area of the shaded portion in the following figures.
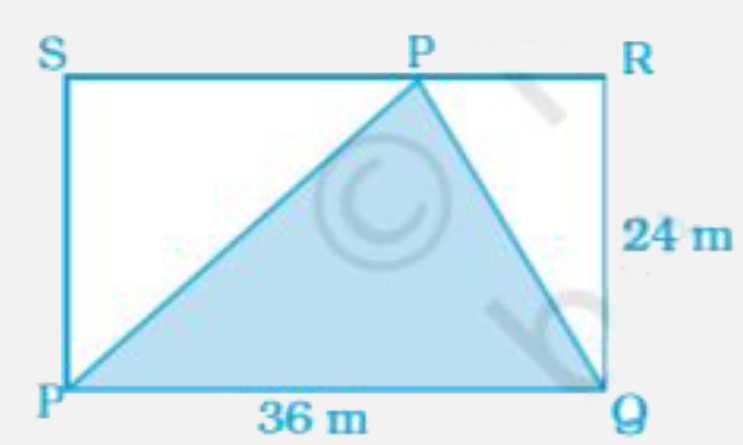
View SolutionFind the area of the shaded portion in the following figures.
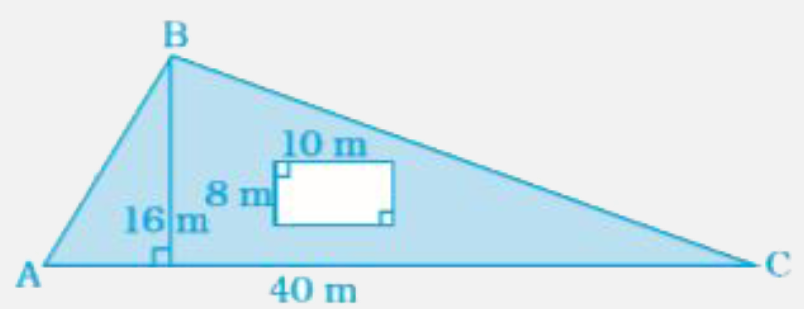
View SolutionFind the area of the shaded portion in the following figures.
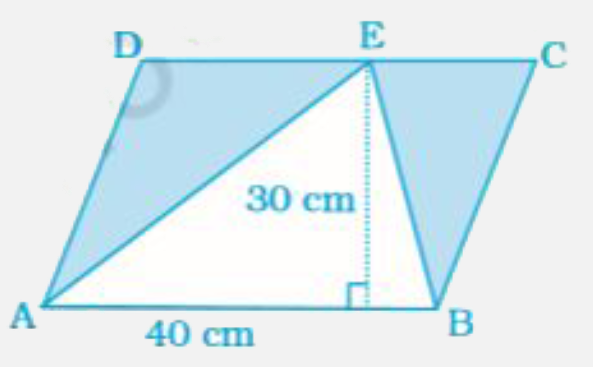
View SolutionFind the area of the shaded portion in the following figures.

View SolutionFind the area of the shaded portion in the following figures.
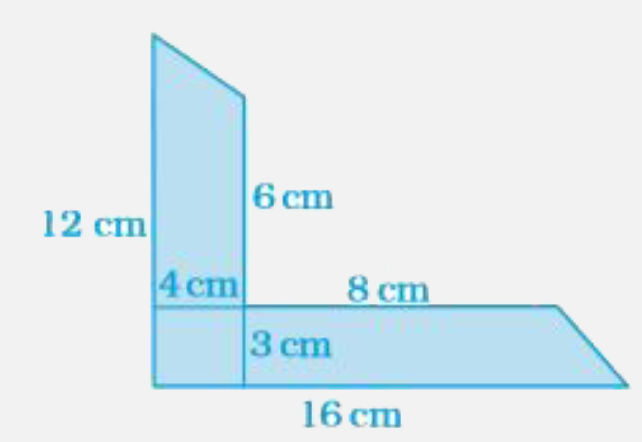
View SolutionFind the area of the shaded portion in the following figures.
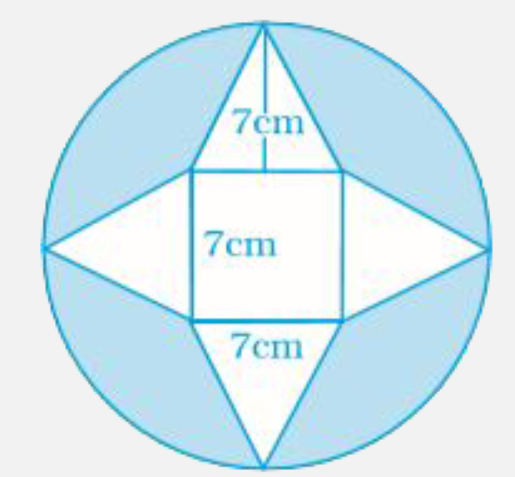
View SolutionFind the area of the shaded portion in the following figures.
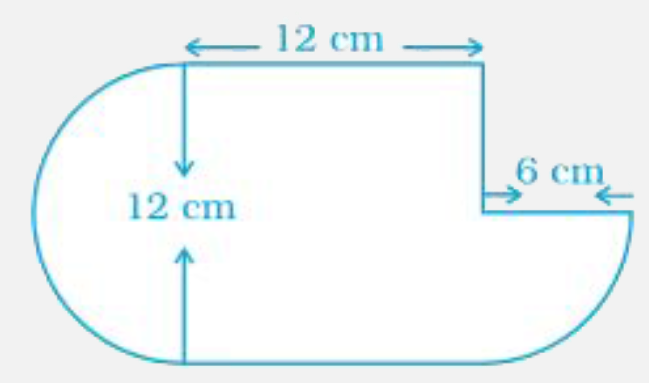
View SolutionFind the area of the following figures.
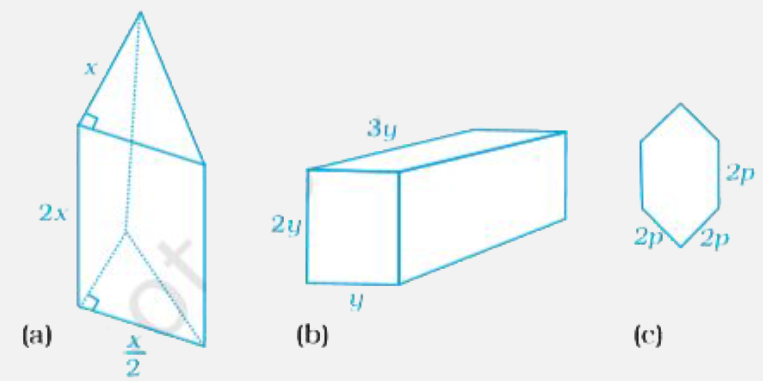
View SolutionFind the volume of each of the given figure if volume = base area × height.
View SolutionA cube of side 5 cm is cut into as many 1 cm cubes as possible. What is the ratio of the surface area of the original cube to that of the sum of the surface areas of the smaller cubes?
View SolutionA square sheet of paper is converted into a cylinder by rolling it along its side.What is the ratio of the base radius to the side of the square?
View SolutionHow many cubic metres of earth must be dug to construct a well 7 m deep and of diameter 2.8 m?
View SolutionThe radius and height of a cylinder are in the ratio 3:2 and its volume is 19,404 `cm^3`. Find its radius and height.
View SolutionThe thickness of a hollow metallic cylinder is 2 cm. It is 70 cm long with outer radius of 14 cm. Find the volume of the metal used in making the cylinder, assuming that it is open at both the ends. Also find its weight if the metal weighs 8 g per `cm^3`.
View SolutionRadius of a cylinder is r and the height is h. Find the change in the volume if the
height is doubled.
View SolutionRadius of a cylinder is r and the height is h. Find the change in the volume if the
height is doubled and the radius is halved.
View SolutionRadius of a cylinder is r and the height is h. Find the change in the volume if the
height remains same and the radius is halved.
View SolutionIf the length of each edge of a cube is tripled, what will be the change in its volume?
View SolutionA carpenter makes a box which has a volume of 13,400 `cm^3`. The base has an area of 670 `cm^2`. What is the height of the box?
View SolutionA cuboidal tin box opened at the top has dimensions `20 cm xx 16 cm xx 14 cm`. What is the total area of metal sheet required to make 10 such boxes?
View SolutionFind the capacity of water tank, in litres, whose dimensions are 4.2 m, 3 m and 1.8 m?
View SolutionHow many cubes each of side 0.5 m are required to build a cube of volume 8 `m^3` ?
View SolutionA wooden box (including the lid) has external dimensions 40 cm by 34 cm by 30 cm. If the wood is 1 cm thick, how many cm3 of wood is used in it?
View Solution
EXERCISES questions and complete solutions for chapter MENSURATION of NCERT EXEMPLAR of Class 8