Complete Solutions to QUESTIONS of chapter TRIANGLES of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | TRIANGLES |
| SELINA PUBLICATION | QUESTIONS |
| Number Of Questions | 8 |
| Academic Year | 2023-24 |
P is any point in the angle ABC such that the perpendicular drawn from P on AB and BC are equal. Prove that BP bisects angle ABC.
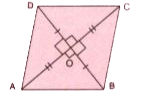
View SolutionIf the diagonals of a quadrilateral bisect each other at right angle, prove that the quadrilateral is a rhombus.
A rhombus has all its four sides equal.
View SolutionIn triangle ABC, the sides AB and AC are equal. If P is a point on AB and Q is a point on AC such that AP = AQ, prove that :
(i) triangle APC and AQB are congruent.
(ii) triangle BPC and CQB are congruent.

View SolutionIn the given figure, AC = AE, AB = AD and `angle BAD = angle EAC`. Show that : BC = DE.

View SolutionUse the information given in the adjoining figure, to prove :
(i) `Delta DBC ~= Delta EAC`.
(ii) DC = EC.
View SolutionThe given figure shows a parallelogram ABCD. Squares ABPQ and ADRS are drawn on sides AB and AD of the parallelogram ABCD. Prove that :
(i) `angle SAQ = angle ABC`
(ii) SQ = AC

View SolutionIn the given figure, ABCD and ABEF are parallelograms. If O is the mid-point of BC, show that : DC = CF = FE.
View SolutionIn the given figure, ABCD is a square. M is the mid-point of AB and PQ is perpendicular to CM. CB produced meets PQ at point Q. Prove that :
(i) PA = BQ
(ii) CP = AB + PA

View Solution
QUESTIONS questions and complete solutions for chapter TRIANGLES of ICSE of Class 9