Complete Solutions to 3 MARKS QUESTIONS of chapter TRIANGLES of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | TRIANGLES |
| OSWAL | 3 MARKS QUESTIONS |
| Number Of Questions | 11 |
| Academic Year | 2023-24 |
The perpendicular bisectors of the sides of a triangle ABC meet at I. Prove that : IA = IB = IC.
View SolutionIf AP bisects angle BAC and M is any point on AP, prove that the perpendiculars drawn from M to AB and AC are equal.
View SolutionIn the following figure, `BL=CM`
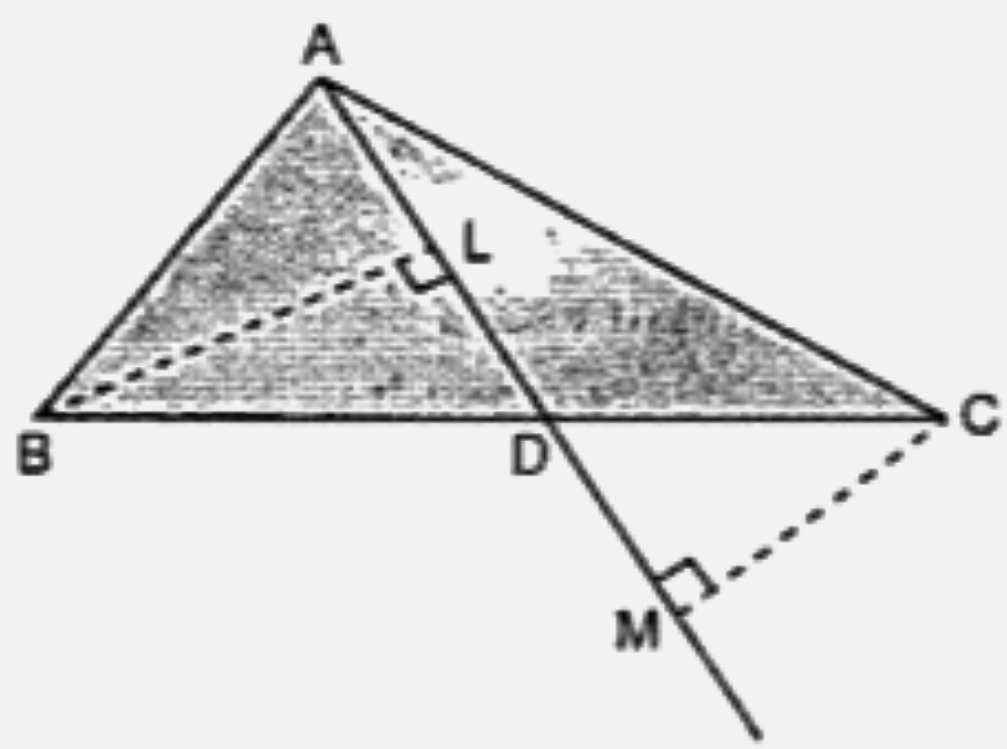
Prove that AD is a Median of triangle ABC
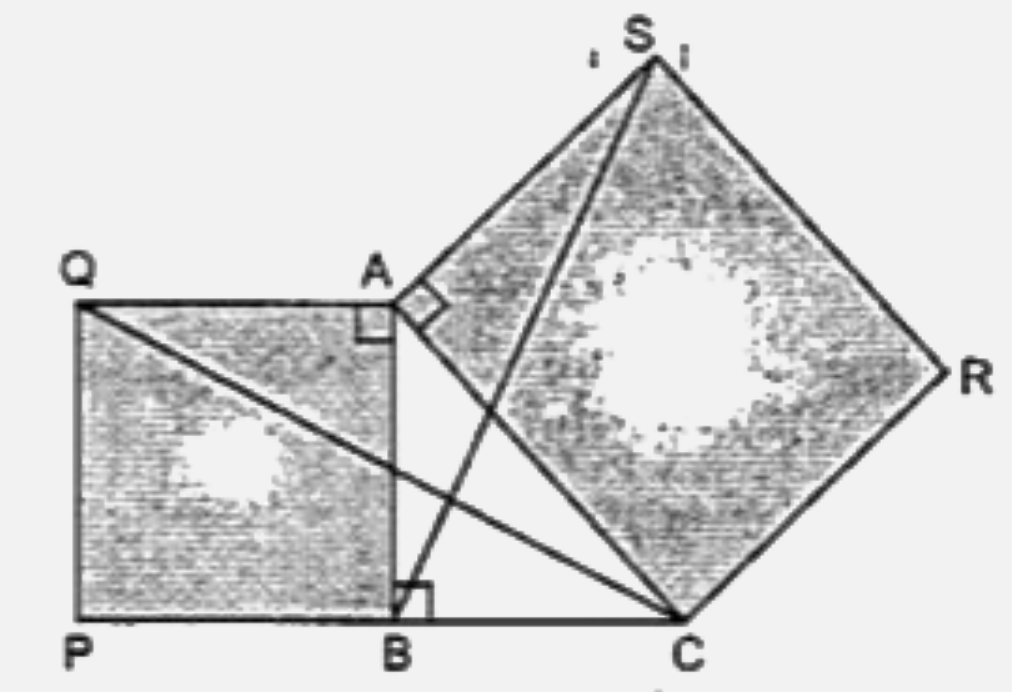
View SolutionIn the figure, given below, triangle ABC is right-angled at B. ABPQ and ACRS are squares.
Prove that :
`DeltaACQ` and `DeltaASB` are congruent
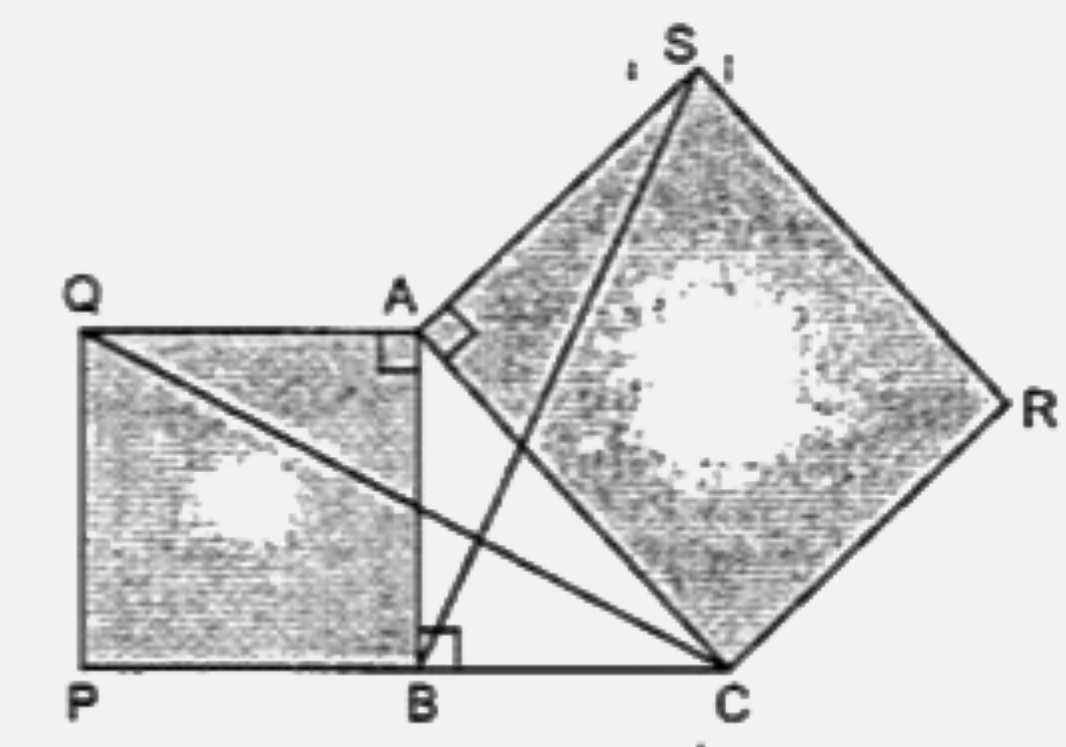
View SolutionIn the figure, given below, triangle ABC is right-angled at B. ABPQ and ACRS are squares.
Prove that :
`CQ=BS`
View SolutionABCD is a parallelogram. The sides AB and AD are produced to E and F respectively, such that AB = BE and AD = DF. Prove that : `Delta BEC ~= Delta DCF`.
View SolutionPQRS is a parallelogram. L and M are points on PQ and SR respectively such that PL = MR. Show that LM and QS bisect each other.
View SolutionIn the following figure, ABC is an equilateral triangle in which QP is parallel to AC. Side AC is produced upto point R so that CR = BP.
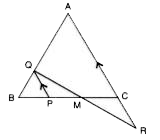
Prove that QR bisects PC.
View SolutionIn `DeltaABC,AB=AC` and the bisectors of angles B and C intersect at point O. Prove that
`BO=OC`
View SolutionIn `Delta ABC`, AB = AC and the bisectors of angles B and C intersect at point O. Prove that :
(i) BO = CO
(ii) AO bisects angle BAC.
View SolutionIn the following, AB=EF, BC=De and `angleE=90^(@)`
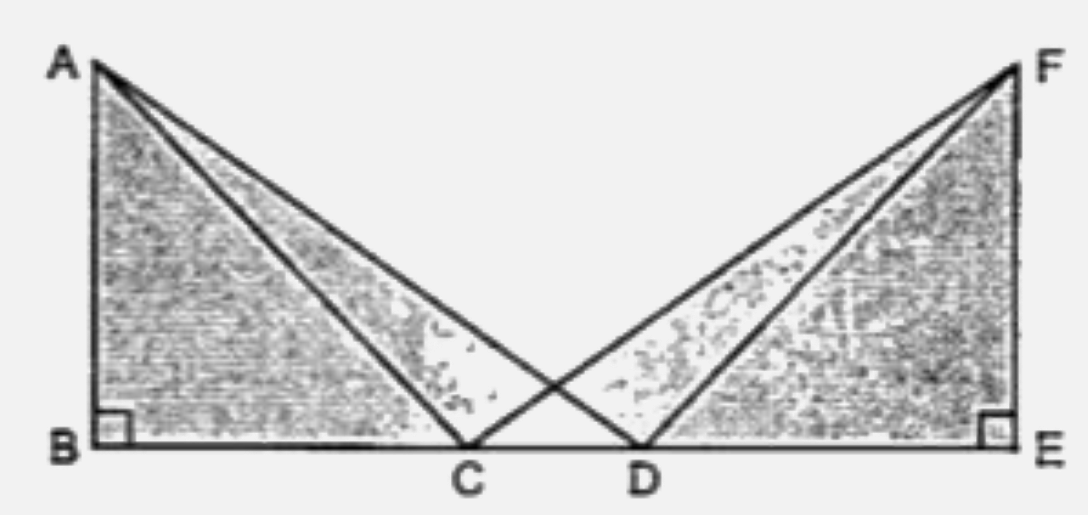
Prove that AD=FC
View Solution
3 MARKS QUESTIONS questions and complete solutions for chapter TRIANGLES of ICSE of Class 9