Complete Solutions to EXERCISE 9(B) of chapter TRIANGLES of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | TRIANGLES |
| SELINA PUBLICATION | EXERCISE 9(B) |
| Number Of Questions | 20 |
| Academic Year | 2023-24 |
On the sides AB and AC of triangle ABC, equilateral triangles ABD and ACE are drawn. Prove that :
(i) `angle CAD = angle BAE`
(ii) CD = BE
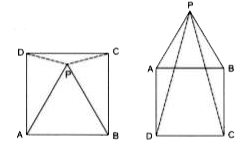
View SolutionIn the following diagrams, ABCD is a square and APB is an equilateral triangle. In each case,
(i) Prove that : `Delta APD ~= Delta BPC`
(ii) Find the angles of `Delta DPC`
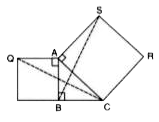
View SolutionIn the figure, given below, triangle ABC is right-angled at B. ABPQ and ACRS are squares. Prove that :
(i) `Delta ACQ and Delta ASB` are congruent.
(ii) CQ = BS
View SolutionIn a `Delta ABC`, BD is the median to the side AC, BD is produced to E such that BD = DE. Prove that : AE is parallel to BC.
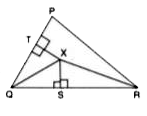
View SolutionIn the adjoining figure, QX and RX are the bisectors of the angles Q and R respectively of the triangle PQR.
If `XS bot QR and XT bot PQ`, prove that :
`Delta XTQ ~= Delta XSQ`
View SolutionIn the parallelogram ABCD, the angles A and C are obtuse. Points X and Y are taken on the diagonal BD such that the angles XAD and YCB are right angles. Prove that : XA = YC
View SolutionABCD is a parallelogram. The sides AB and AD are produced to E and F respectively, such that AB = BE and AD = DF. Prove that : `Delta BEC ~= Delta DCF`.
View SolutionIn the following figures, the sides AB and BC and the median AD of triangle ABC are respectively equal to the sides PQ and QR and median PS of the triangle PQR. Prove that `Delta ABC and Delta PQR` are congruent.

View SolutionIn the following diagram, AP and BQ are equal and parallel to each other.
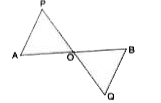
Prove that :
(i) `Delta AOP ~= Delta BOQ`
(ii) AB and PQ bisect each other.
View SolutionIn the following figure, OA = OC and AB = BC. Prove that :
(i) `angle AOB = 90^(@)`
(ii) `Delta AOD ~= Delta COD`
(iii) AD = CD

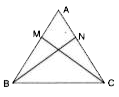
View SolutionThe following figure shows a triangle ABC in which AB = AC. M is a point on AB and N is a point on AC such that BM = CN. Prove that :
(i) AM = AN
(ii) `Delta AMC ~= Delta ANB`
(iii) BN = CM
(iv) `Delta BMC ~= Delta CNB`
View SolutionIn a triangle ABC, AB = BC, AD is perpendicular to side BC and CE is perpendicular to side AB. Prove that : AD = CE.
View SolutionPQRS is a parallelogram. L and M are points on PQ and SR respectively such that PL = MR. Show that LM and QS bisect each other.
View SolutionIn the following figure, ABC is an equilateral triangle in which QP is parallel to AC. Side AC is produced upto point R so that CR = BP.
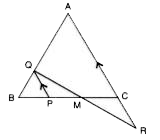
Prove that QR bisects PC.
View SolutionIn the following figure, `angle A = angle C` and AB = BC.
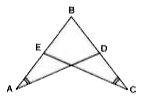
Prove that : `Delta ABD ~= Delta CBE`
View SolutionAD and BC are equal perpendiculars to a line segment AB. If AD and BC are on different sides of AB prove that CD bisects AB.
View SolutionIn `Delta ABC`, AB = AC and the bisectors of angles B and C intersect at point O. Prove that :
(i) BO = CO
(ii) AO bisects angle BAC.
View SolutionIn the following figure, AB = EF, BC = DE and `angle B = angle E = 90^(@)`.
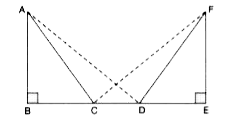
Pove that AD = FC.
View SolutionA point O is taken inside a rhombus ABCD such that its distances from the vertices B and D are equal. Show that AOC is a straight line.
View SolutionIn quadrilateral ABCD, AD = BC and BD = CA. Prove that :
(i) `angle ADB = angle BCA`
(ii) `angle DAB = angle CBA`
View Solution
EXERCISE 9(B) questions and complete solutions for chapter TRIANGLES of ICSE of Class 9