Complete Solutions to 4 MARKS QUESTIONS of chapter TRIANGLES of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | TRIANGLES |
| OSWAL | 4 MARKS QUESTIONS |
| Number Of Questions | 24 |
| Academic Year | 2023-24 |
In a triangle ABC, D is mid-point of BC, AD is produced upto E so that DE = AD. Prove that :
(i) `Delta ABD and Delta ECD` are congruent.
(ii) AB = EC
(iii) AB is parallel to EC.
View SolutionIn a triangle ABC,D is the mid - point of BC, AD is produced upto E so that DE = AD.
Prove that :
`AB=EC`
View SolutionIn a triangle ABC, D is mid-point of BC, AD is produced upto E so that DE = AD. Prove that :
(i) `Delta ABD and Delta ECD` are congruent.
(ii) AB = EC
(iii) AB is parallel to EC.
View SolutionFrom the given diagram, in which ABCD is a Parallelogram, ABL is a line segment and E is a mid - point of BC.
Prove that :
`DeltaDCE~=DeltaLBE`

View SolutionFrom the given diagram, in which ABCD is a Parallelogram, ABL is a line segment and E is a mid - point of BC.
Prove that :
`AB=BL`
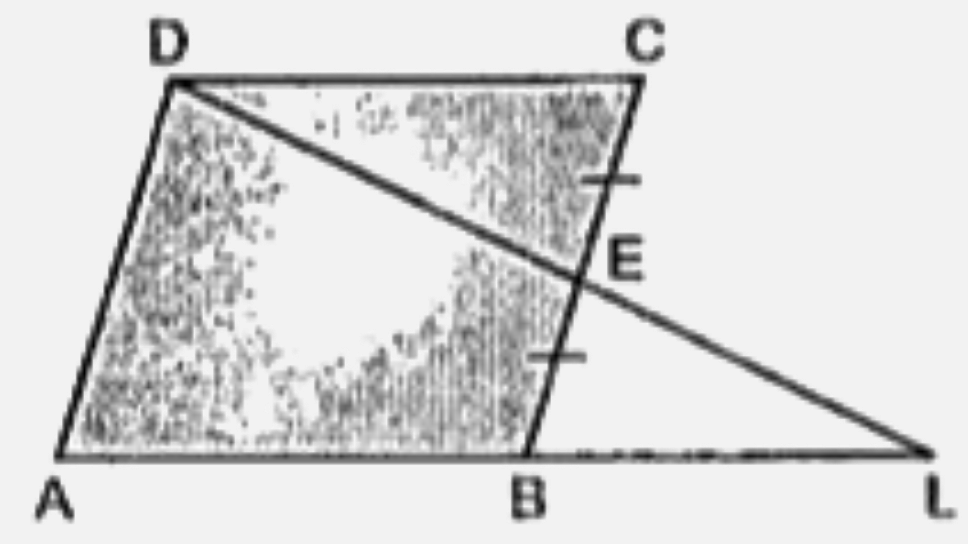
View SolutionFrom the given diagram, in which ABCD is a Parallelogram, ABL is a line segment and E is a mid - point of BC.
Prove that :
`AL=2DC`
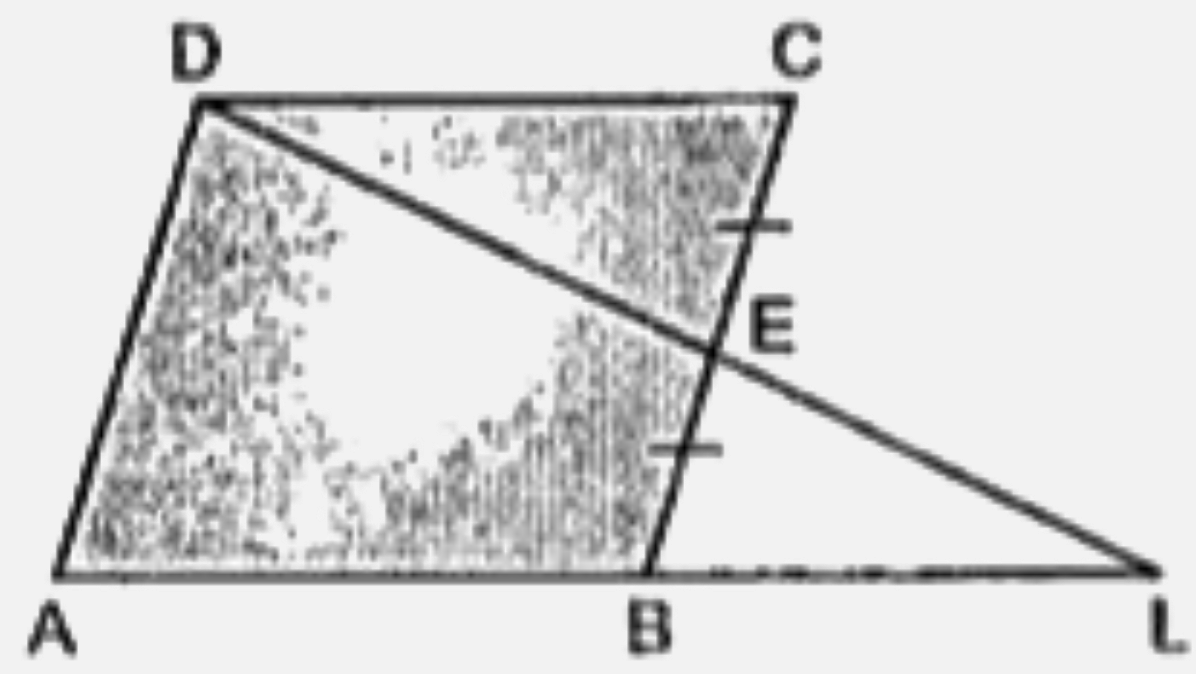
View SolutionIn the given figure, AB = DB and AC = DC. If `angleABD=58^(@),angleDBC=(2x-4)^(@),angleACB=y+15^(@)` and `angleDCB=63^(@)`, Find the value of x and y.

View SolutionIn the following figure, AB = AC and AD is perpendicular to BC. BE bisects angle B and EF is perpendicular to AB.
Prove that : ED=EF
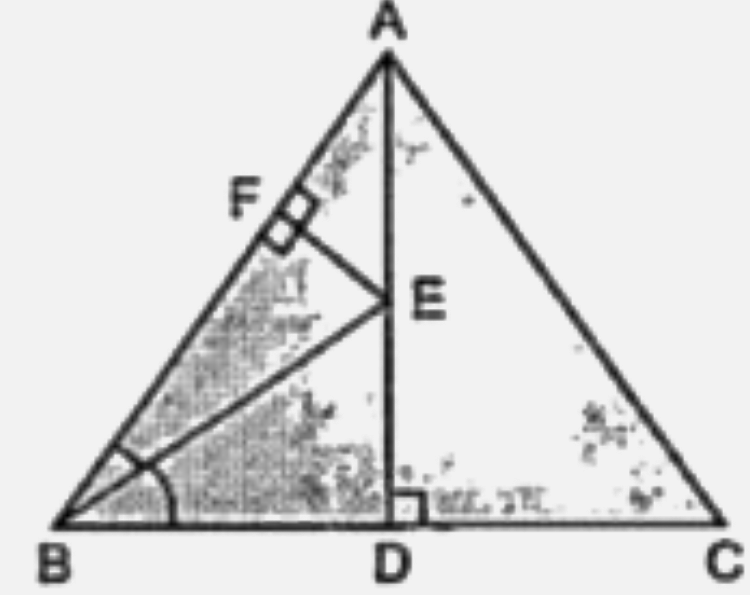
View SolutionIn the following figure, AB = AC and AD is perpendicular to BC. BE bisects angle B and EF is perpendicular to AB.
Prove that :
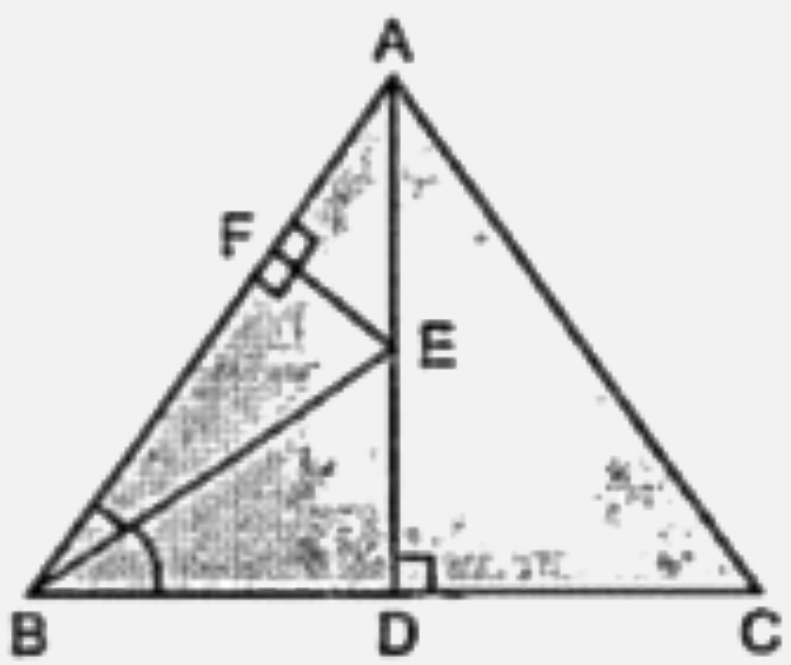
ED=EF
View SolutionOn the sides AB and AC of triangle ABC, equilateral triangles ABD and ACE are drawn. Prove that :
`angleCAD=angleBAE`
View SolutionOn the sides AB and AC of triangle ABC, equilateral triangles ABD and ACE are drawn. Prove that :
(i) `angle CAD = angle BAE`
(ii) CD = BE
View SolutionIn the adjoining figure, OX and RX are the bisectors of the angle Q and R respectively of the triangle PQR. If `XS bot QR` and `XTbotPQ`.
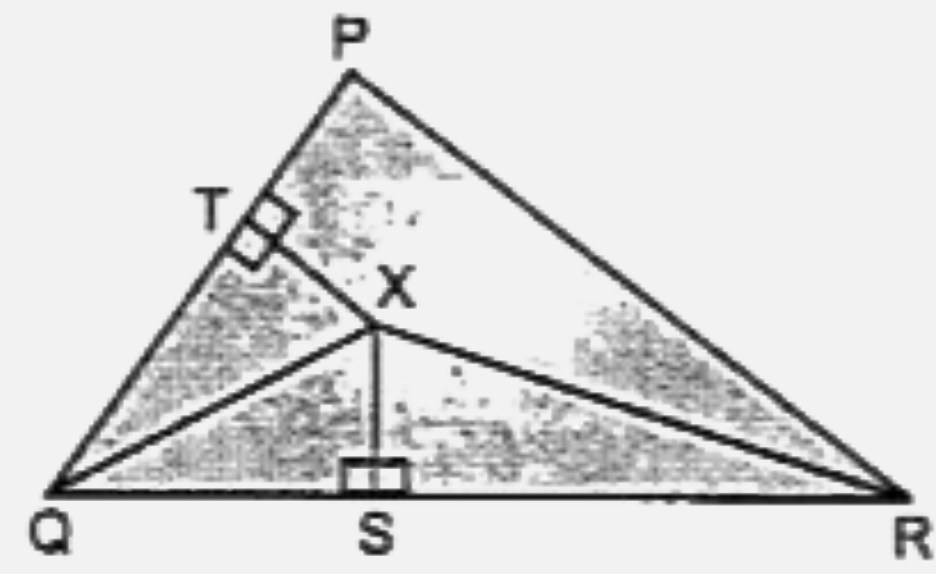
Prove that :
`DeltaXTQ~=DeltaXSQ`
View SolutionIn the adjoining figure, OX and RX are the bisectors of the angle Q and R respectively of the triangle PQR. If `XS bot QR` and `XTbotPQ`.
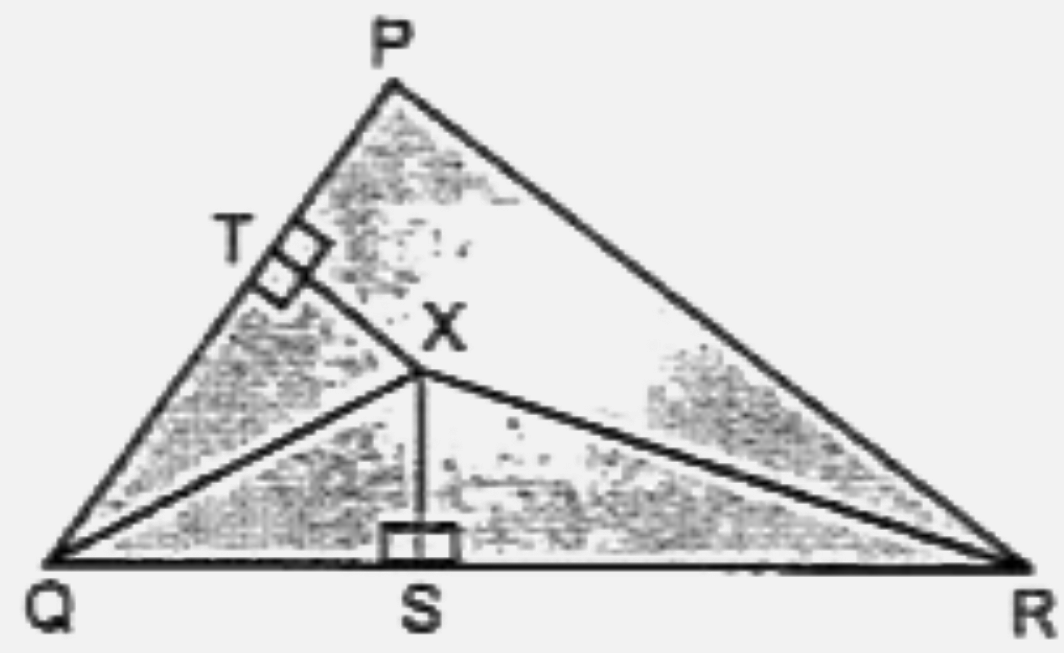
Prove that :
PX bisects angle P.
View SolutionIn the following figure, `OA=OC` and `AB=BC`.
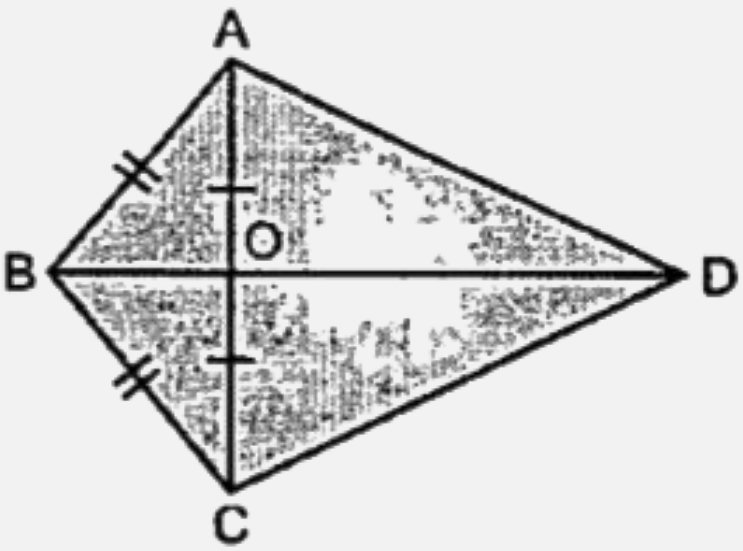
Prove that :
`angleAOB=90^(@)`
View SolutionIn the following figure, `OA=OC` and `AB=BC`.

Prove that :
`DeltaAOD~=DeltaCOD`
View SolutionIn the following figure, `OA=OC` and `AB=BC`.
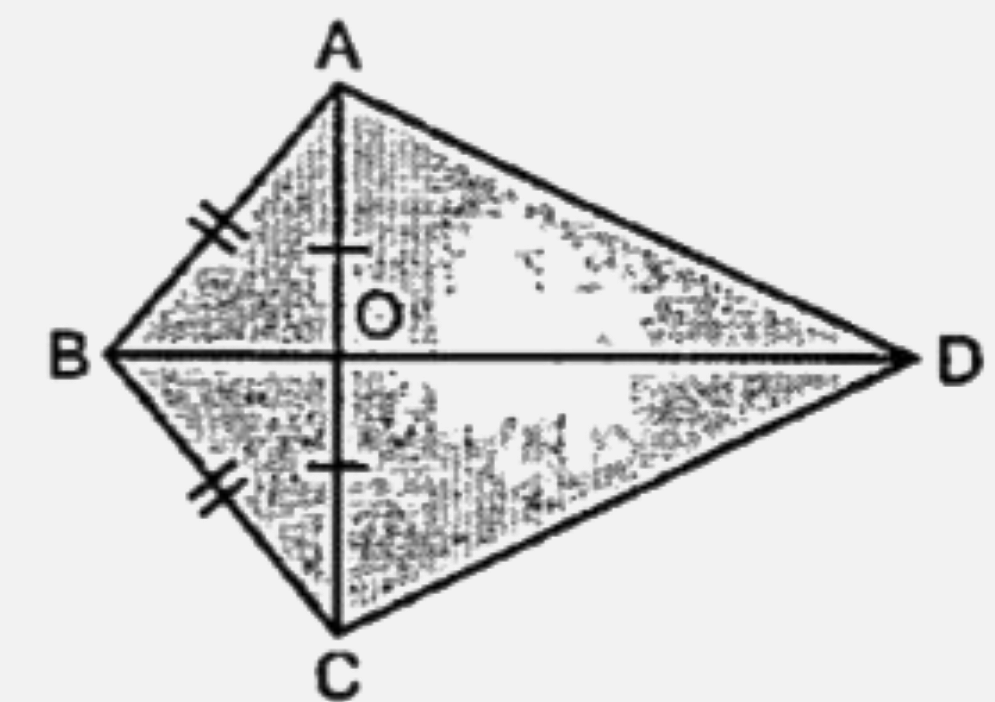
Prove that :
AD=CD
View SolutionThe following figure shows a triangle ABC in which AB=AC. M is a point on AB and N is a point on AC such that BM = CN. Prove that
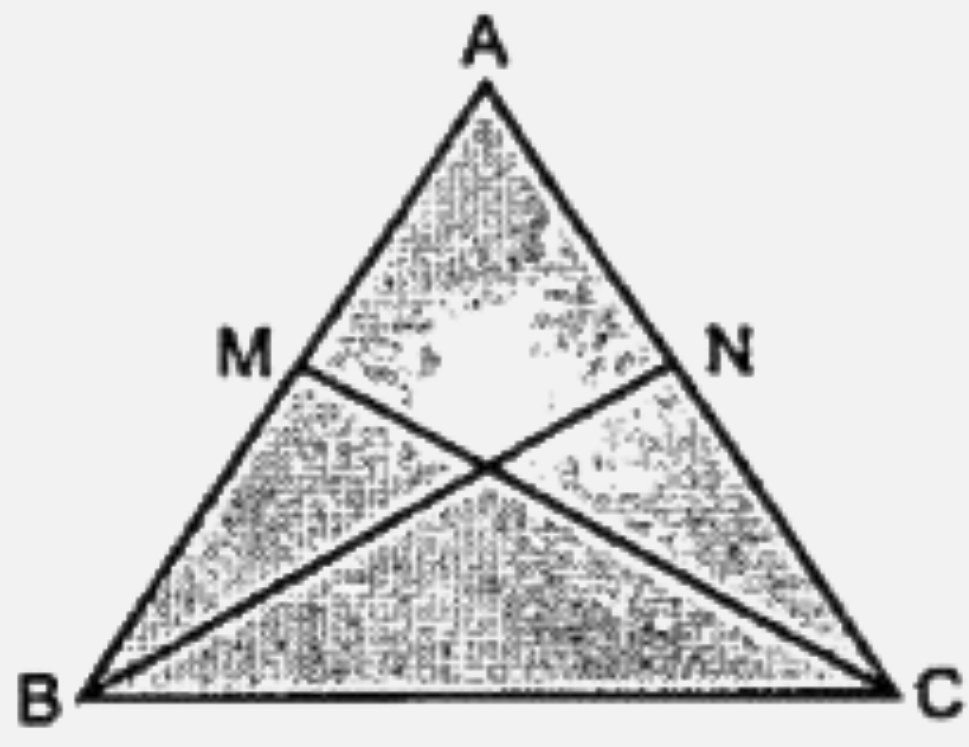
`AM=AN`
View SolutionThe following figure shows a triangle ABC in which AB=AC. M is a point on AB and N is a point on AC such that BM = CN. Prove that
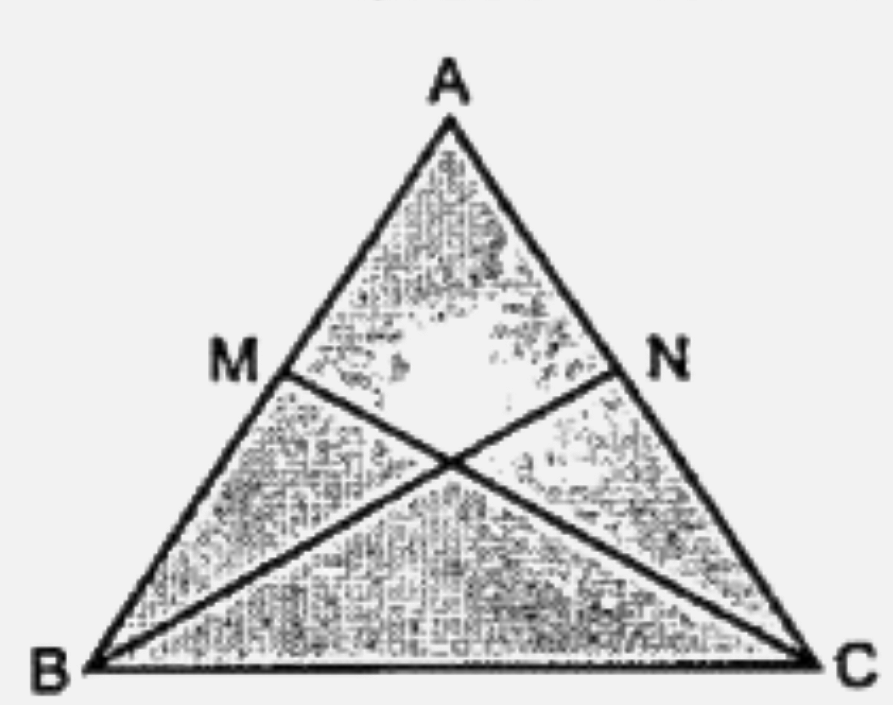
`DeltaAMC~=DeltaANB`
View SolutionThe following figure shows a triangle ABC in which AB=AC. M is a point on AB and N is a point on AC such that BM = CN. Prove that

`BN=CM`
View SolutionThe following figure shows a triangle ABC in which AB=AC. M is a point on AB and N is a point on AC such that BM = CN. Prove that

`DeltaBMC~=DeltaCNB`
View SolutionIn the given diagram ABCD is a parallelogram. `DeltaAPD` and `DeltaBQC` are equilateral triangles.
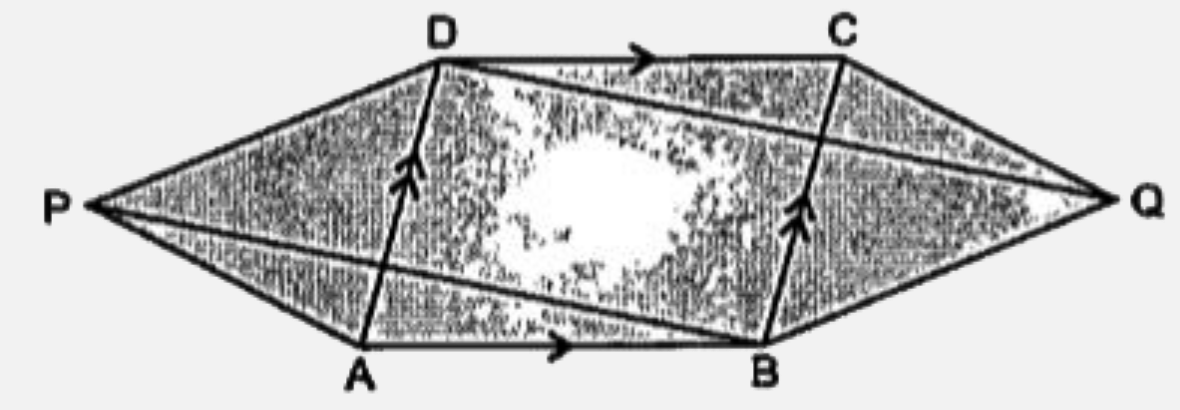
Prove that :
`anglePAB=angleQCD`
View SolutionIn the given diagram ABCD is a parallelogram. `DeltaAPD` and `DeltaBQC` are equilateral triangles.
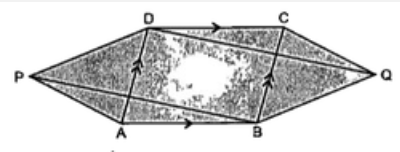
Prove that :
`PB=QD`
View SolutionIn the given figure ABC is a triangle and D is the mid-point of BC. AD is produced to E. BM and CN are two perpendiculars dropped from B and C respectively on AE.

Prove that :
`DeltaBMD~=DeltaCND`
View SolutionIn the given figure ABC is a triangle and D is the mid-point of BC. AD is produced to E. BM and CN are two perpendiculars dropped from B and C respectively on AE.
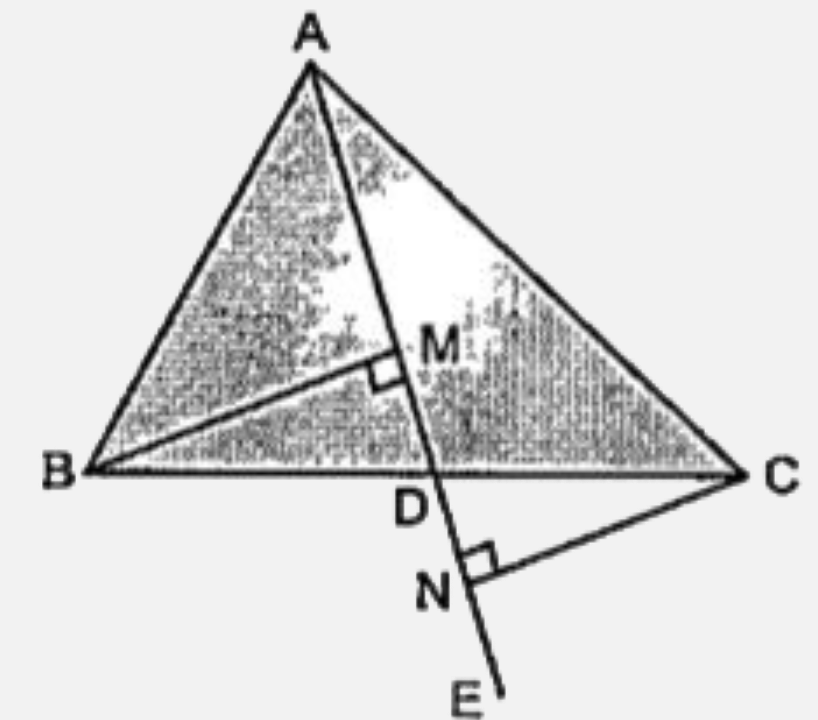
Prove that :
`BM=CN`
View Solution
4 MARKS QUESTIONS questions and complete solutions for chapter TRIANGLES of ICSE of Class 9