Complete Solutions to EXERCISE 9(A) of chapter TRIANGLES of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | TRIANGLES |
| SELINA PUBLICATION | EXERCISE 9(A) |
| Number Of Questions | 15 |
| Academic Year | 2023-24 |
Which of the following pairs of triangles are congruent ? In each case, state the condition of congruency :
(a) In `Delta ABC and Delta DEF`, AB = DE, BC = EF and `angle B = angle E`.
(b) In `Delta ABC and Delta DEF, angle B = angle E = 90^(@)`, AC = DF and BC = EF.
(c) In `Delta ABC and Delta QRP`, AB = QR, `angle B = angle R and angle C = angle P`.
(d) In `Delta ABC and Delta PQR`, AB = PQ, AC = PR and BC = QR.
(e) In `Delta ABC and Delta PQR`, BC = QR, `angle A = 90^(@), angle C = angle R = 40^(@) and angle Q = 50^(@)`.
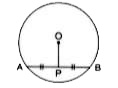
View SolutionThe given figure shows a circle with centre O. P is mid-point of chord AB.
Show that OP is perpendicular to AB.
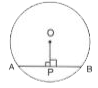
View SolutionThe following figure shows a circle with centre O.
If OP is perpendicular to AB, prove that AP = BP.
View SolutionIn a triangle ABC, D is mid-point of BC, AD is produced upto E so that DE = AD. Prove that :
(i) `Delta ABD and Delta ECD` are congruent.
(ii) AB = EC
(iii) AB is parallel to EC.
View SolutionA triangle ABC has `angle B = angle C`. Prove that :
(i) the perpendiculars from the mid-point of BC to AB and AC are equal.
(ii) the perpendicular from B and C to the opposite sides are equal.
View SolutionThe perpendicular bisectors of the sides of a triangle ABC meet at I. Prove that : IA = IB = IC.
View SolutionA line segment AB is bisected at point P and through point P another line segment PQ, which is perpendicular to AB, is drawn. Show that : QA = QB.
View SolutionIf AP bisects angle BAC and M is any point on AP, prove that the perpendiculars drawn from M to AB and AC are equal.
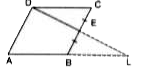
View SolutionFrom the given diagram, in which ABCD is a parallelgram, ABL is a line segment and E is mid point of BC. Prove that :
(i) `Delta DCE ~= Delta LBE`
(ii) AB = BL
(iii) AL = 2DC
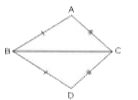
View SolutionIn the given figure, AB = DB and AC = DC. If `angle ABD = 58^(@), angle DBC = (2x - 4)^(@), angle ACB = y + 15^(@) and angle DCB = 63^(@)`, find the values of x and y.
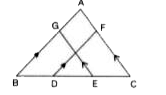
View SolutionIn the given figure : AB//FD, AC//GE and BD = CE, prove that :
(i) BG = DF
(ii) CF = EG
View SolutionIn a triangle ABC, AB = AC. Show that the altitude AD is median also.
View SolutionIn the following figure, BL = CM.

Prove that AD is a median of triangle ABC.
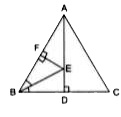
View SolutionIn the following figure, AB = AC and AD is perpendicular to BC. BE bisects angle B and EF is perpendicular to AB. Prove that :
(i) BD = CD
(ii) ED = EF
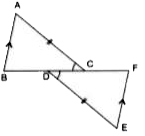
View SolutionUse the information in the given figure to prove :
(i) AB = FE
(ii) BD = CF
View Solution
EXERCISE 9(A) questions and complete solutions for chapter TRIANGLES of ICSE of Class 9