Complete Solutions to Solved Examples of chapter AREA OF PARALLELOGRAMS AND TRIANGLES of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | AREA OF PARALLELOGRAMS AND TRIANGLES |
| NAGEEN PRAKASHAN | Solved Examples |
| Number Of Questions | 16 |
| Academic Year | 2023-24 |
The area of a parallelogram is `32 cm^(2)`. If its altitude is twice of its base, then find the altitude
View SolutionThe area of a parallelogram is `150cm^(2)`. If the ratio of its base and corresponding altitude is `3 : 2`, find the length of base and altitude
View SolutionThe diagonals of a parallelogram `A B C D` intersect at `Odot` A line through `O` meets `A B\ ` in `x\ a n d\ C D` in `Ydot` Show that `a r\ (A X Y X)=1/2(a r|""|^(gm)\ \ A B C D)`
View SolutionShow that a median of a triangle divides it into two triangles of equal areas.
View SolutionThe diagonals AC and BD of a quadrilateral ABCD intersect at point 'O'. If BO = OD, then prove that the areas of `Delta ABC and Delta ADC` are equal
View SolutionIf each diagonals of a quadrilateral separates it into two triangles of equal area then show that the quadrilateral is a parallelogram.
View SolutionThe vertices of a rectangle PQRS are joined from an interior point 'O'. Prove that the sum of the area of two opposite triangles so formed is equal to the sum of the areas of remaining two triangles
View SolutionIn the adjoining figure D, E and F are the mid-points of the sides BC, CA and AB respectively of `Delta ABC`. Prove that:
(i) `square BDEF` is a parallelogram
(ii) area of `Delta DEF = (1)/(4) xx " area of " Delta ABC`
(iii) area of `square BDEF = (1)/(2) xx " area of " Delta ABC`

View SolutionIn the adjoining figure, AD is the median of `Delta ABC` and X be any point on side AD. Prove that:
area `(Delta ABX) = " area " (Delta ACX)`

View SolutionThe medians of `Delta ABC` intersect at point G. Prove that:
area of `Delta AGB = (1)/(3) xx " area of " Delta ABC`
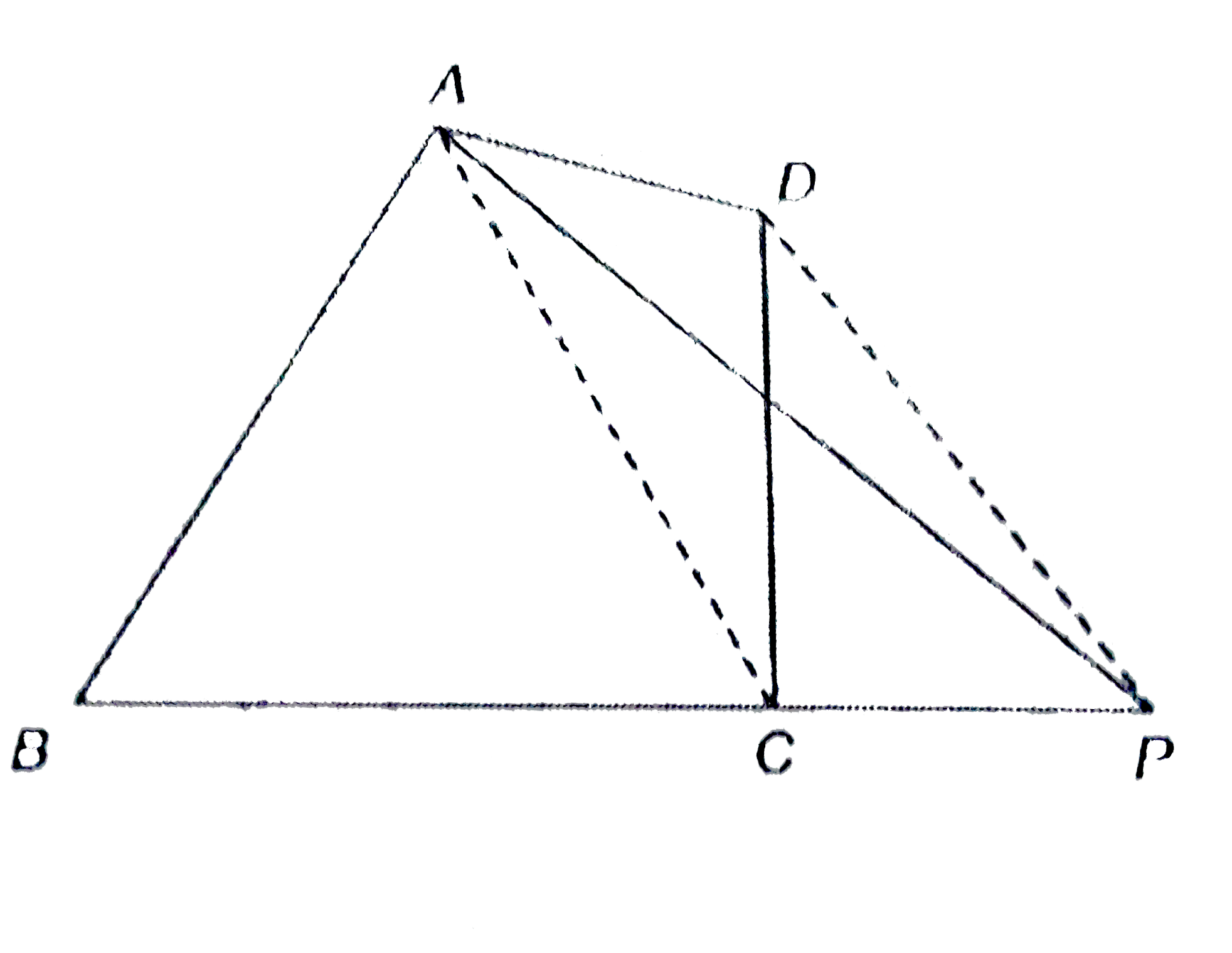
View SolutionIn the figure, ABCD is a quadrilateral. A line DP drawn parallel to diagonal AC from point D, meet BC produced at P. Prove that:
area of `Delta ABP = " area of " square ABCD`
View SolutionXY is a line parallel to side BC of a triangle ABC. If `B E\ ||\ A C`and `C F\ ||\ A B`meet XY at E and F respectively, show that `a r\ (A B E)\ =\ a r\ (A C F)`
View SolutionA point D is taken on the side BC of a `DeltaABC` such that `BD = 2DC.` Prove that `ar(DeltaABD) = 2 ar (DeltaADC)`
View SolutionXY is a line parallel to side BC of a triangle ABC. If `B E\ ||\ A C`and `C F\ ||\ A B`meet XY at E and F respectively, show that `a r\ (A B E)\ =\ a r\ (A C F)`
View SolutionIn the figure, ABC and BDE are two equilateral triangle such that D is the mid-point of BC. If AE intersects BC at F, show that:
(i) `ar(DeltaBDE) = (1)/(4) ar(DeltaABC)` (ii) `ar(DeltaBDE) = (1)/(2) ar(DeltaBAE)`
(iii) `ar(DeltaABC) = 2 ar(DeltaBEC)` (iv) `ar(DeltaBFE) = ar(DeltaAFD)`
(v) `ar(DeltaBFE) = 2ar(DeltaFED)` (vi) `ar(DeltaFED) = (1)/(8) ar(DeltaAFC)`

View SolutionABCD is a parallelogram. X and Y are mid-points of BC and CD. Prove that `ar(triangleAXY)=3/8ar(||^[gm] ABCD)`
View Solution
Solved Examples questions and complete solutions for chapter AREA OF PARALLELOGRAMS AND TRIANGLES of NAGEEN MATHS (HINGLISH) of Class 9