Complete Solutions to Exercise 10.3 of chapter CIRCLES of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | CIRCLES |
| NCERT EXEMPLAR | Exercise 10.3 |
| Number Of Questions | 20 |
| Academic Year | 2023-24 |
If two arcs of a circle (or of congruent circles) are congruent, then corresponding chords are equal.
View SolutionIf the perpendicular bisector of a chord AB of a circle PXAQBY intersects the circle at P and Q, prove that arc `PXA cong"arc "PYB`.
View SolutionA, B and C are three points on a circle. Prove that the perpendicular bisectors of AB, BC and CA are concurrent.
View SolutionTwo chords `A B` and `A C` of a circle are equal. Prove that the centre of the circle lies on the angle bisector of `/_B A Cdot`
View SolutionIf a line segment joining mid-points of two chords of a circle passes through the centre of the circle, prove that the two chords are parallel.
View Solution`ABCD` is such a quadrilateral that A is the centre of the circle passing through `B, C and D`. Prove that `/_CBD+ /_CDB =1/2 /_BAD`.
View SolutionIf `O` is the circumcentre of a ` A B C` and `O D_|_B C ,` prove that `/_B O D=/_adot`
View SolutionOn a common hypotenuse AB, two right angled triangles, ACB and ADB are situated on opposite sides. Prove that `angleBAC=angleBDC`.
View SolutionTwo chords AB and AC of a circle subtends angles equal to `90^(@) and 150^(@)`, respectively at the centre. Find`angleBAC`, if AB and AC lie on the opposite sides of the centre.
View SolutionIf BM and CN are the perpendiculars drawn on the sides AC and BC of the `Delta ABC`, prove that the points B, C, M and N are concyclic.
View SolutionIf a line is drawn parallel to the base of an isosceles triangle to intersect its equal sides, prove that the quadrilateral, so formed is cyclic.
View SolutionIf the two sides of a pair of opposite sides of a cyclic quadrilateral are equal, prove that its diagonals are equal.
View SolutionThe circumcentre of the `DeltaABC" is O. Prove that "angleOBC+angleBAC=90^(@)`.
View SolutionA chord of a circle is equal to the radius of the circle find the angle subtended by the chord at a point on the minor arc and also at a point on the major arc.
View SolutionIn figure, `angleADC=130^(@)" and chord BC=chord BE. Find "angleCBE`.

View SolutionIn figure, `angleACB=40^(@) ." Find "angleOAB`.

View SolutionIn Figure, `A B C D` is a cyclic quadrilateral whose side `A B` is a diameter of the circle through `A ,\ B ,\ C ,\ Ddot` If `(/_A D C)=130^0,` find `/_B A C`
View SolutionTwo circles whose centres are `O` and `O '` intersect at `Pdot` Through `P ,` a line `l` parallel to `O O '` intersecting the circles at `C\ a n d\ D` is drawn. Prove that `C D=2\ O O '`
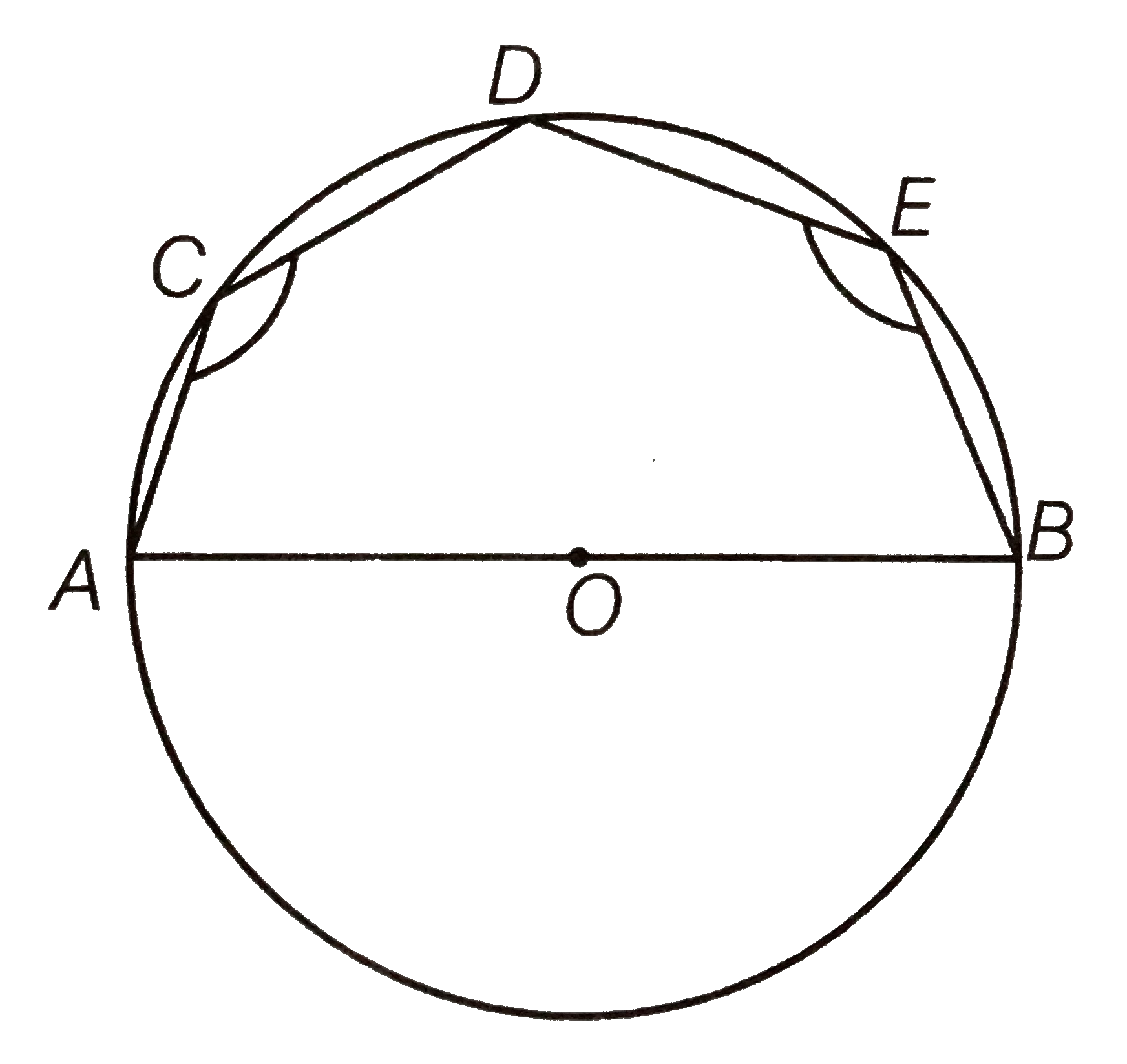
View SolutionIn figure, AOB is a diameter of the circle and C, D, E are any three points on the semi-circle. Find the value of `angleACD+ angleBED`.
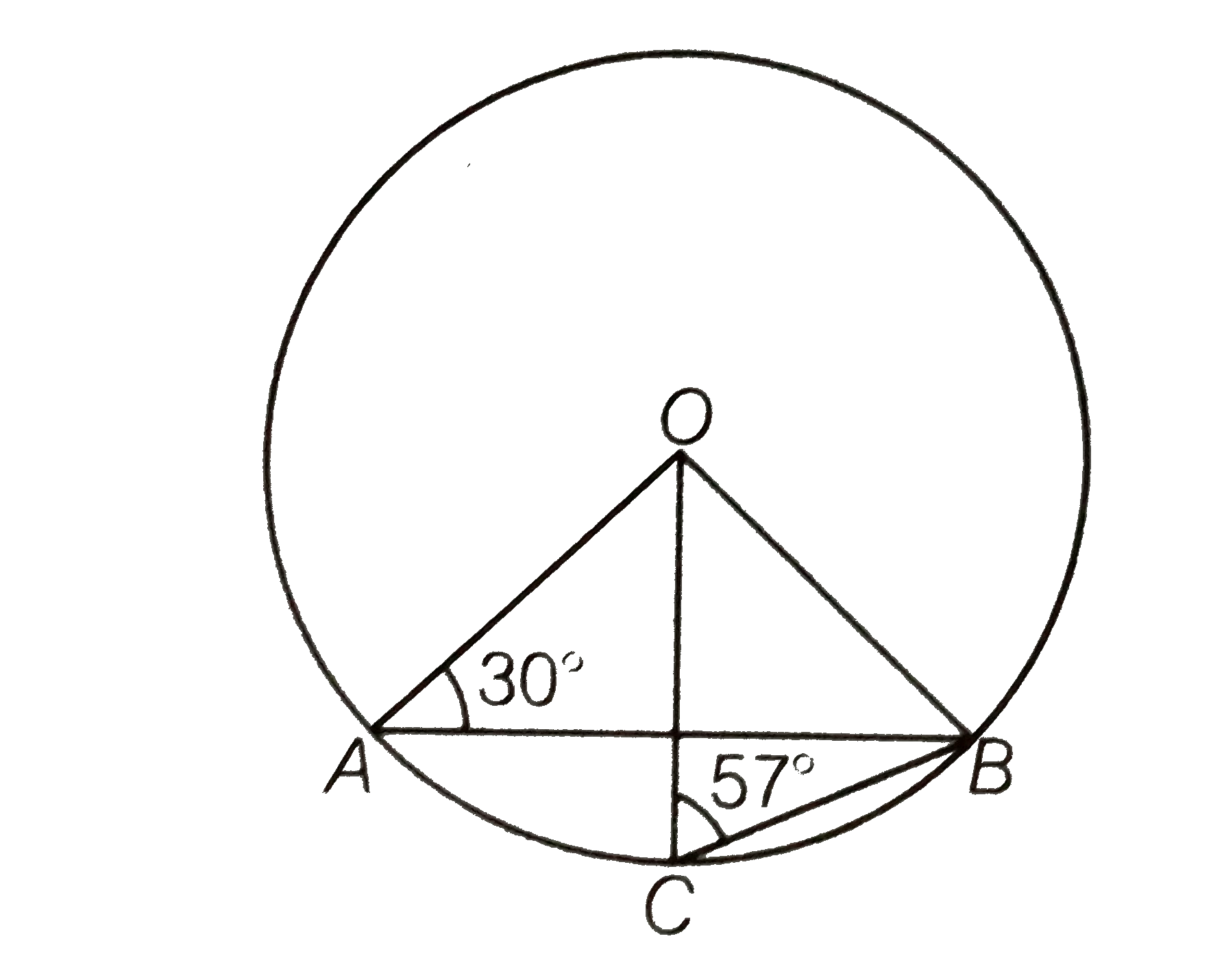
View SolutionIn figure, `angleOAB=30^(@) and angleOCB=57^(@)." Find "angleBOC and angleAOC`.
View Solution
Exercise 10.3 questions and complete solutions for chapter CIRCLES of NCERT MATHS (ENGLISH) of Class 9