If BM and CN are the perpendiculars drawn on the sides AC and BC of the ΔABC, prove that the points B, C, M and N are concyclic.
To prove that points B, C, M, and N are concyclic, we will follow these steps:
Step 1: Draw Triangle ABC
We start by drawing triangle ABC with points A, B, and C.
Step 2: Draw Perpendiculars BM and CN
Next, we draw the perpendiculars BM and CN from points B and C to the sides AC and BC, respectively. Let M be the foot of the perpendicular from B to AC, and N be the foot of the perpendicular from C to BC.
Step 3: Consider BC as the Diameter of a Circle
Now, we will consider the line segment BC as the diameter of a circle. According to the properties of circles, any angle subtended by a diameter on the circumference of the circle is a right angle.
Step 4: Show Angles at Points M and N
Since BM is perpendicular to AC, angle BMC is a right angle (90 degrees). Similarly, since CN is perpendicular to BC, angle CBN is also a right angle (90 degrees).
Step 5: Conclude that M and N Lie on the Circle
From the above steps, we have established that angles BMC and CBN are both right angles. Therefore, points M and N must lie on the circle with diameter BC, as both angles subtended by the diameter are right angles.
Step 6: Conclude that B, C, M, and N are Concyclic
Since points B, C, M, and N all lie on the same circle, we conclude that these points are concyclic.
Final Conclusion
Thus, we have proved that points B, C, M, and N are concyclic.
---
We start by drawing triangle ABC with points A, B, and C.
Next, we draw the perpendiculars BM and CN from points B and C to the sides AC and BC, respectively. Let M be the foot of the perpendicular from B to AC, and N be the foot of the perpendicular from C to BC.
Now, we will consider the line segment BC as the diameter of a circle. According to the properties of circles, any angle subtended by a diameter on the circumference of the circle is a right angle.
Since BM is perpendicular to AC, angle BMC is a right angle (90 degrees). Similarly, since CN is perpendicular to BC, angle CBN is also a right angle (90 degrees).
From the above steps, we have established that angles BMC and CBN are both right angles. Therefore, points M and N must lie on the circle with diameter BC, as both angles subtended by the diameter are right angles.
Since points B, C, M, and N all lie on the same circle, we conclude that these points are concyclic.
Thus, we have proved that points B, C, M, and N are concyclic.
Topper's Solved these Questions
- CIRCLESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CIRCLESEXERCISE - Exercise 10.4
14 Videos
- CIRCLESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CIRCLESEXERCISE - Exercise 10.2
10 Videos
- Areas of Parallelograms and TrianglesBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - Areas of Parallelograms and TrianglesEXERCISE - Exercise-9.4 Long Answer Type Questions
10 Videos
- CONSTRUCTIONSBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CONSTRUCTIONSEXERCISE - Long Answer Type Questions
5 Videos
Similar Questions
In Figure, ABC is a triangle in which AB=AC. Point DandE are points on the sides ABandAC respectively such that AD=AE. Show that the points B,C,EandD are concyclic.
View SolutionIn the adjoining figure, BM and CN are the altitudes drawn to the sides AC and AB respectively of ΔABC. If BM=CN, prove that ΔABC is isosceles.

View SolutionABC is an isosceles triangle in which AB=AC. If D and E are the mid-points of AB and AC respectively, Prove that the points B, C, D and E are concyclic.
View SolutionPerpendicular bisectors of the sides AB and AC of a triangle ABC meet at O.
What do you call the point ?
View SolutionAL, BM and CN are perpendicular from angular points of a triangle ABC on the opposite sides BC, CA and AB respectively. Δ is the area of triangle ABC, (r ) and R are the inradius and circumradius.
If perimeters of ΔLMNandΔABCanλandμ, then the value of λμ is
View SolutionAL, BM and CN are perpendicular from angular points of a triangle ABC on the opposite sides BC, CA and AB respectively. Δ is the area of triangle ABC, (r ) and R are the inradius and circumradius.
If area of ΔLMN is Δ', then the value of Δ'Δ is
View SolutionAD, BE and CF are the medians of triangle ABC whose centroid is G. If the points A, F, G and E are concyclic, then prove that 2a2=b2+c2
View SolutionD, E and F are the mid-points of the sides BC, CA and AB respectively of triangle ABC. Prove that:
area of BDEF is half the area of ΔABC.
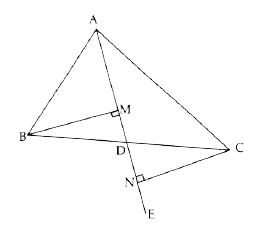
View SolutionIn the given figure ABC is a triangle and D is the mid-point of BC. AD is produced to E. BM and CN are two perpendiculars dropped from B and C respectively on AE.
Prove that : (i) ΔBMD≅ΔCND (ii) BM = CN
View SolutionFrom a point O inside a triangle ABC, perpendiculars OD,OEandOf are drawn to rthe sides BC,CAandAB, respecrtively. Prove that the perpendiculars from A,B,andC to the sides EF,FDandDE are concurrent.
View Solution