The circumcentre of the .
Given A circle is circumscribed on a having centre O.
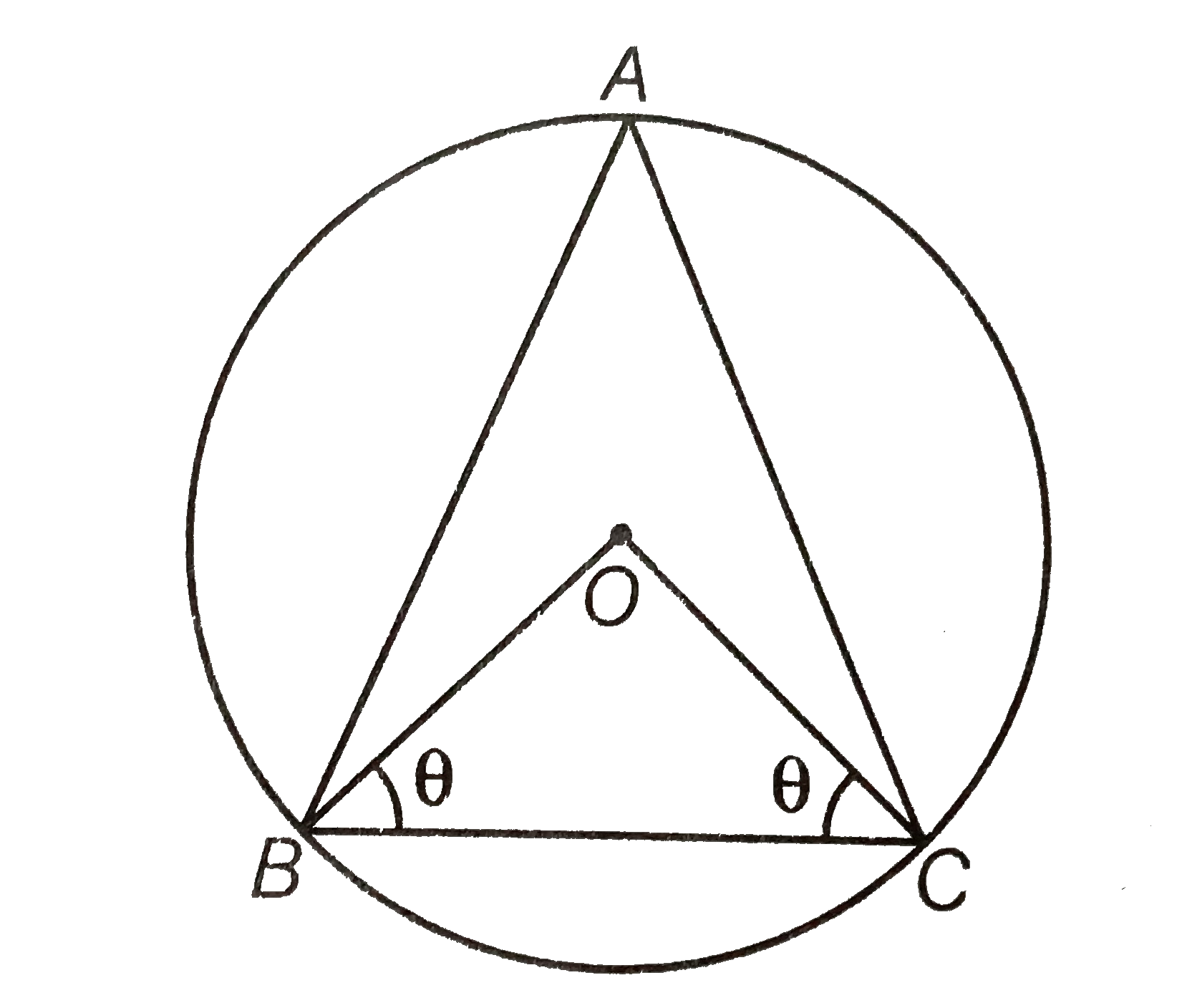
To prove
Construction Join BO and CO.
Proof Let …(i)
In
[by angle sum property of a triangle is ]
We know that, in a circle, the angle subtended by an arc at the centre is twice the angle subtended by it at the remaining part of the circle.
[from Eq. (i)]
Topper's Solved these Questions
- CIRCLESBook:NCERT EXEMPLAR ENGLISHChapter:CIRCLESExercise:Exercise 10.4
Explore 14 Videos
- CIRCLESBook:NCERT EXEMPLAR ENGLISHChapter:CIRCLESExercise:Exercise 10.2
Explore 10 Videos
- Areas of Parallelograms and TrianglesBook:NCERT EXEMPLAR ENGLISHChapter:Areas of Parallelograms and TrianglesExercise:Exercise-9.4 Long Answer Type Questions
Explore 10 Videos
- CONSTRUCTIONSBook:NCERT EXEMPLAR ENGLISHChapter:CONSTRUCTIONSExercise:Long Answer Type Questions
Explore 5 Videos
Similar Questions
The circumcentre of the triangle ABC is O . Prove that ∠OBC+∠BAC=90∘.
View SolutionIn ΔABC, prove that: sinB+sinC>sinA
View SolutionP is any point inside the triangle ABC. Prove that : ∠BPC>∠BAC.
View SolutionIf O is the circumcentre and P the orthocentre of ΔABC, prove that −−→OA+−−→OB+−−→OC=−−→OP.
View SolutionIn a ΔABC,PandQ are the mid-points of ABandAC respectively. If O is the circumcentre of the ΔABC, then the value of (Area of ΔABCArea of ΔOPQ)cotBcotC equal to
View SolutionProve that
tanθtan(90∘−θ)=1
View SolutionIn ΔABC, prove that: bsinB−csinC=asin(B−C)
View SolutionIn ΔABC, bisectors of ∠Band∠C interesct each other at point O. Prove that ∠BOC=90∘+12∠Ai.e.,∠1=90∘+12A
View SolutionIn ΔABC, bisectors of ∠Band∠C interesct each other at point O. Prove that ∠BOC=90∘+12∠Ai.e.,∠1=90∘+12
View SolutionIn ΔABC, prove that: asinA−bsinB=csin(A−B
View Solution