Complete Solutions to Solved Examples of chapter QUADRILATERALS of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | QUADRILATERALS |
| RS AGGARWAL | Solved Examples |
| Number Of Questions | 17 |
| Academic Year | 2023-24 |
Three angles of a quadrilateral measure `110^(@), 82^(@) and 68^(@)`. Find the measure of the fourth angle.
View SolutionThe angles of a quadrilateral are in the ratio `3:5: 9:13.` Find all the angles of the quadrilateral.
View SolutionIn a||gm ABCD, if `angle A = 115^(@), " find " angle B,.`
View SolutionDiagonals AC and BD of a parallelogram ABCD intersect at O. If OA = 3 cm and OD = 2 cm, determine the lengths of AC and BD.
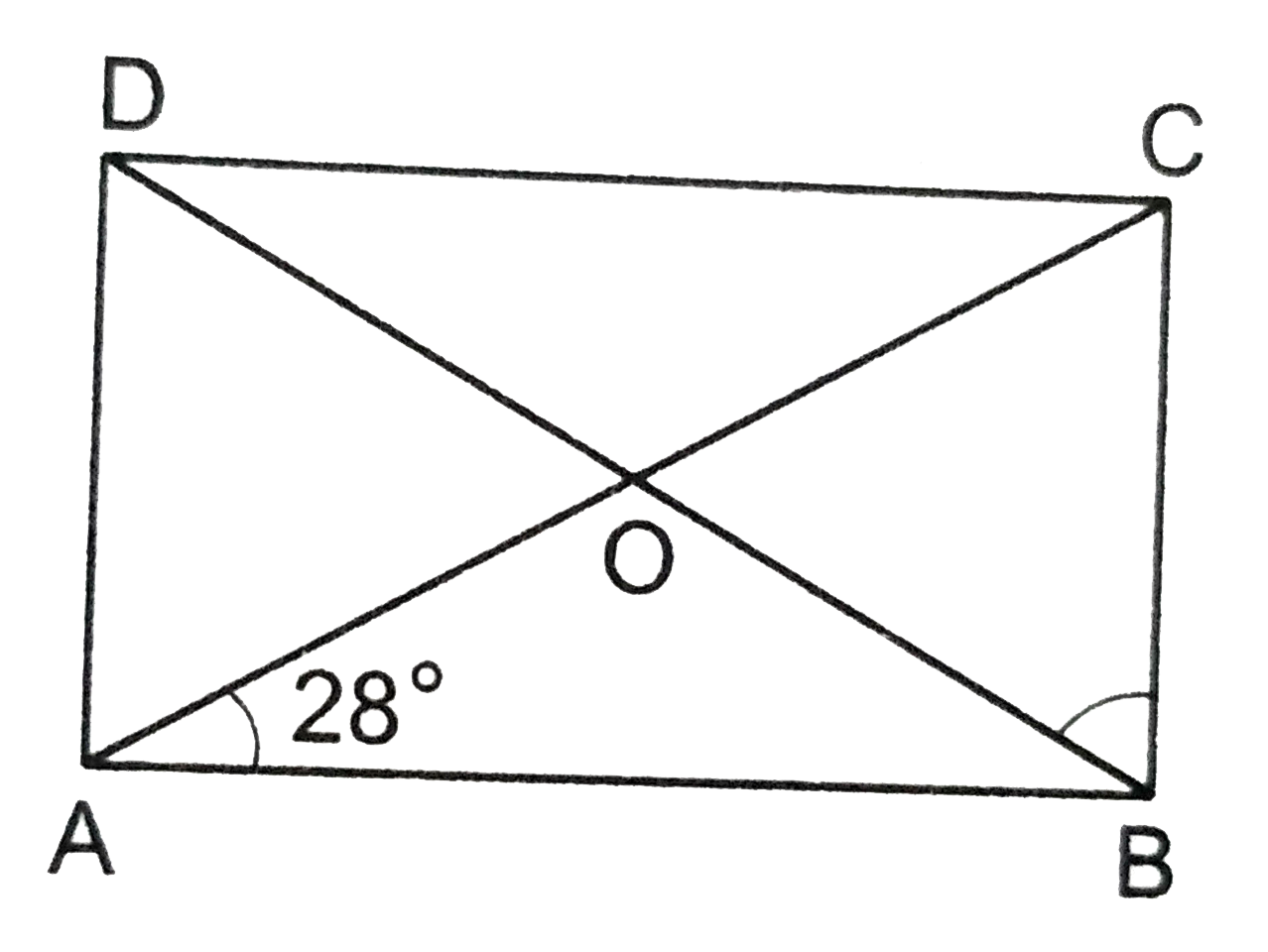
View SolutionIn the adjoining figure, ABCD is a rectangle whose diagonals AC and BD intersect at O. If `angle OAB =28^(@), " find " angle OBC.`
View SolutionThe diagonals `AC` and `BD` of a parallelogram `ABCD` intersect each other at the point O. If `angle DAC = 32^(@) and angle AOB =70^(@), " find " angle DBC.`
View SolutionIn the adjoining figure, ABCD is a rhombus. If `angle A =70^(@), " find " angle CDB. `

View SolutionABCD is a rhombus such that `angle ACB=40^(@). " Find " angle ADB.`
View Solutionlf D, E and F are respectively the midpoints of the sides BC, CA and AB of an equilateral triangle ABC, prove that `triangle DEF` is also an equilateral triangle.
View SolutionIn `DeltaA B C`, D, E and F are respectively the mid-points of sides AB, BC and CA. Show that `DeltaA B C`is divided into four congruent triangles by joining D, E and F.
View SolutionLet `A B C` be an isosceles triangle with `A B=A C` and let `D , E ,F` be the mid-points of `B C ,C A` and `A B` respectively. Show that `A D_|_F E` and `A D` is bisected by `F Edot`
View SolutionLet ABC be a triangle, right-angled at B and D be the midpoint of AC. Show that DA = DB = DC.
View SolutionThe figure formed by joining the mid-points of the adjacent sides of a quadrilateral is
View SolutionE and F are respectively the midpoints of the non-parallel sides AD and BC of a trapezium ABCD. Prove that
(i) `EF||AB,`
(ii) `EF=(1)/(2) (AB+CD).`
View SolutionProve that the line joining the mid-points of the diagonals of a trapezium is parallel to the parallel sides of trapezium and is half of their difference.
View SolutionABCD is a trapezium in which `A B\ ||\ D C`, BD is a diagonal and E is the mid-point of AD. A line is drawn through E parallel to AB intersecting BC at F (see Fig. 8.30). Show that F is the mid-point of BC.
View SolutionABC is a triangle right-angled at C. A line through the midpoint P of hypotenuse AB and parallel to BC intersects AC at M. Show that
`"(i) "` M is the midpoint of `AC,`
` "(ii) " MP bot AC ,`
` "(iii) " CP = AP=(1)/(2)AB. `
View Solution
Solved Examples questions and complete solutions for chapter QUADRILATERALS of RS AGGARWAL MATHS (HINGLISH) of Class 9