Complete Solutions to EXERCISE 10C of chapter QUADRILATERALS of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | QUADRILATERALS |
| RS AGGARWAL | EXERCISE 10C |
| Number Of Questions | 18 |
| Academic Year | 2023-24 |
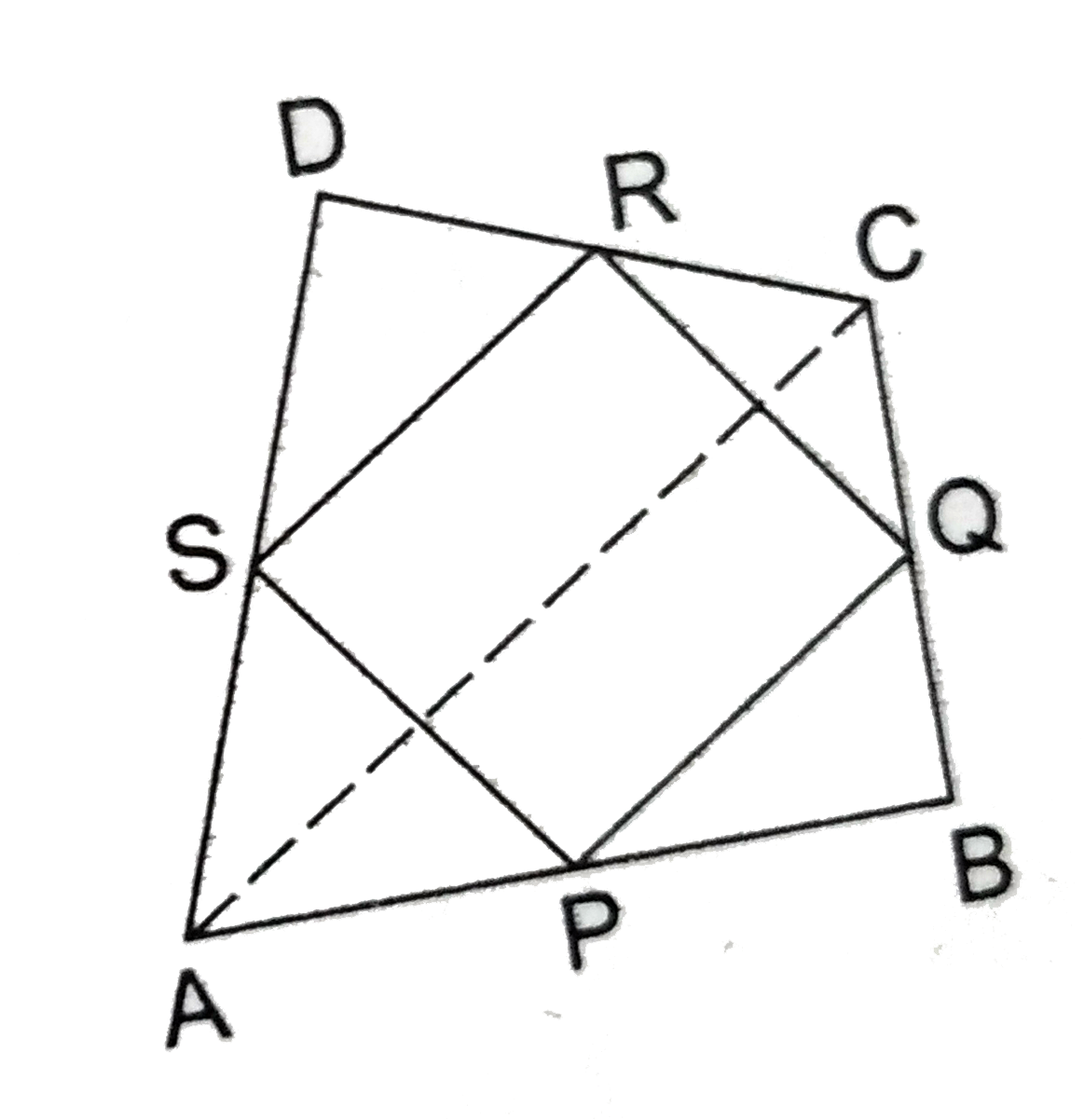
P, Q, R and S are respectively the midpoints of the sides AB, BC, CD and DA of a quadrilateral ABCD. Show that
(i) PQ||AC and ` PQ=(1)/(2) AC `
(ii) PQ||SR
(iii) PQRS is a parallelogram .
View SolutionA square is inscribed in an isosceles right triangle so that the square and the triangle have an angle common. Show that the vertex of the square opposite the vertex of the common angle bisects the hypotenuse
View Solution`ABCD` is a parallelogram, E and F are the mid-points of AB and CD respectively. GH is any line intersecting AD, EF and BC at G, P and H respectively. Prove that `GP=PH.`
View SolutionM and N are points on opposite sides AD and BC of a parallelogram ABCD such that MN passes through the point of intersection O of its diagoinals AC and BD. Show that MN is bisected at O.
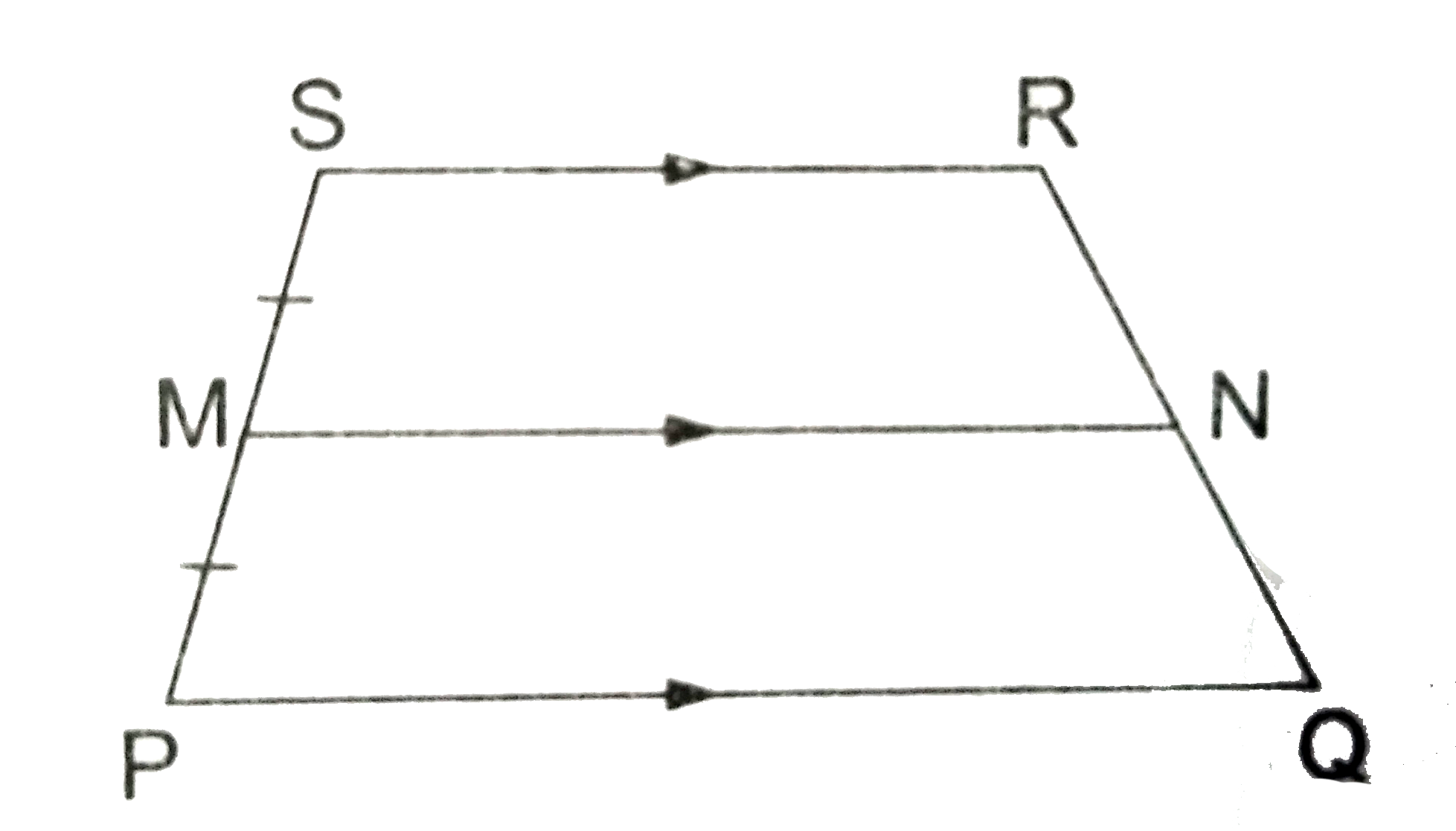
View SolutionIn the adjoining figure, PQRS is a trapezium in which PQ||SR and M is the midpoint of PS. A line segment MN||PQ meets QR at N. Show that N is the midpoint of QR.
View SolutionIn a parallelogram PQRS, PQ = 12 cm and PS = 9 cm. The bisector of `angle P` meet SR in M. PM and QR both when produced meet at T. Find the length of RT.
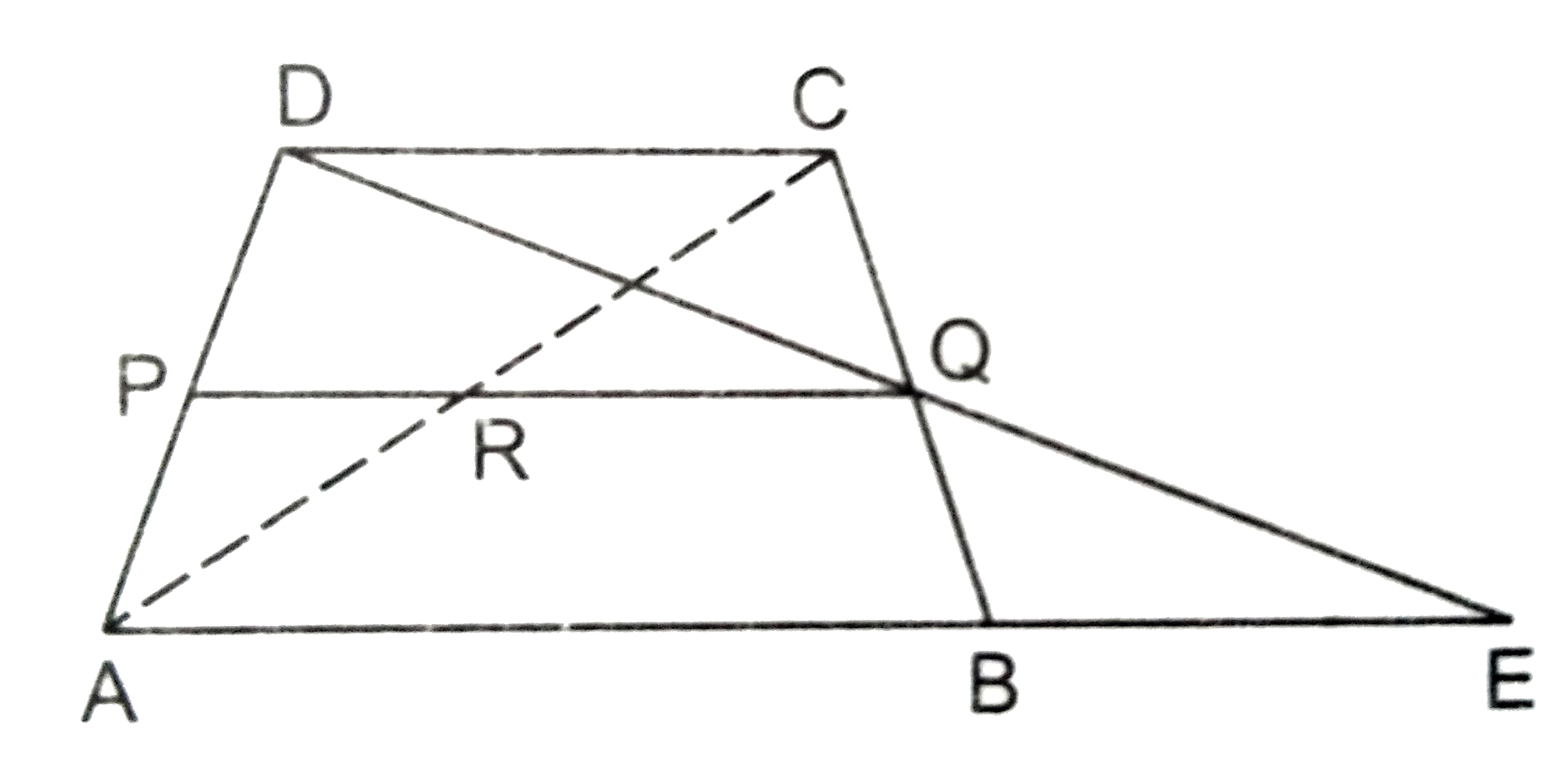
View SolutionIn the adjoining figure, ABCD is a trapezium in which AB||DC and P, Q are the midpoints of AD and BC respectively. DQ and AB when produced meet at E. Also, AC and PQ intersect at R. Prove that (i) DQ = QE, (ii) PR||AB and (iii) AR = RC.
View SolutionIn the adjoining figure, AD is a median of `triangle ABC` and DE||BA. Show that BE is also a median of `triangle ABC.`
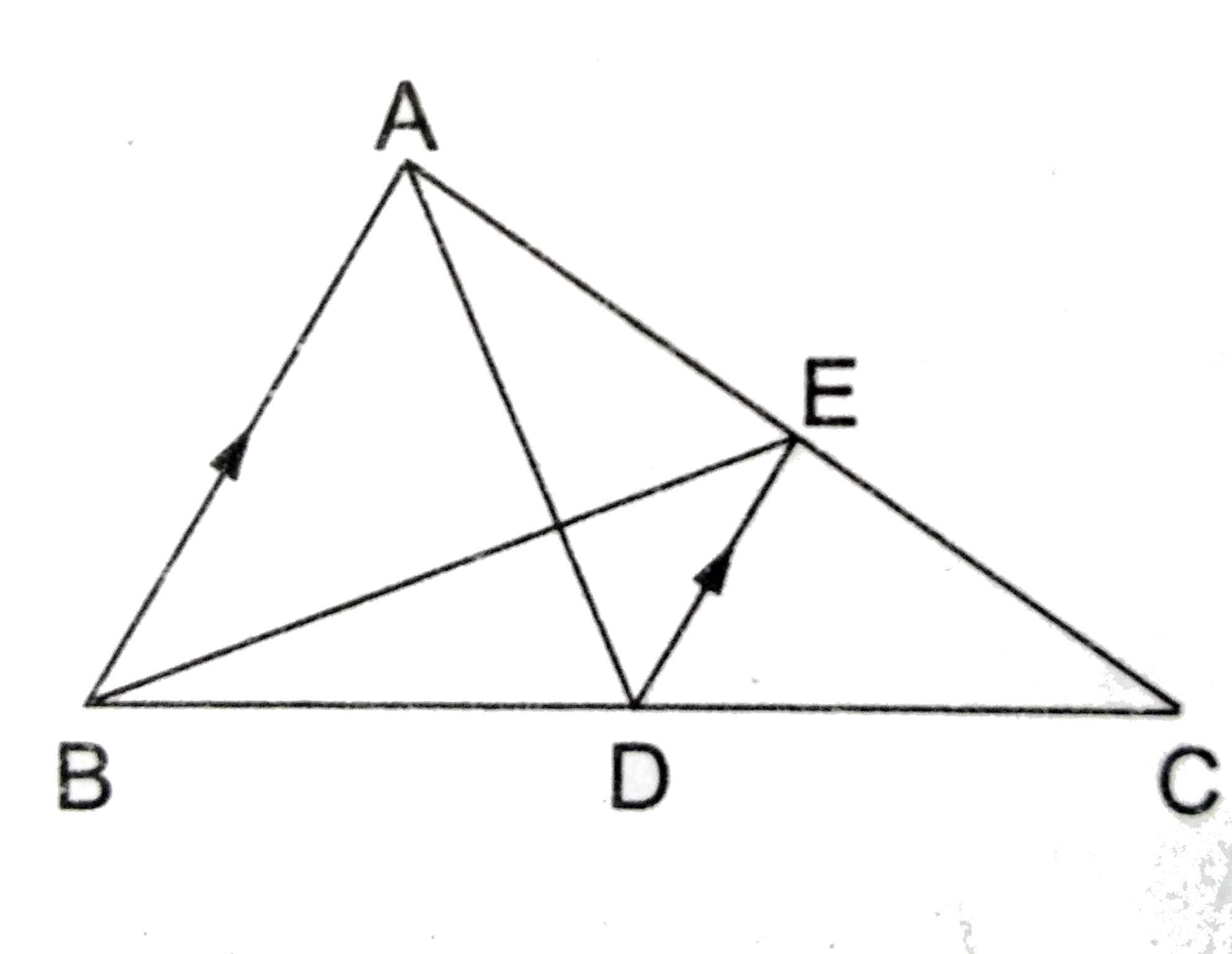
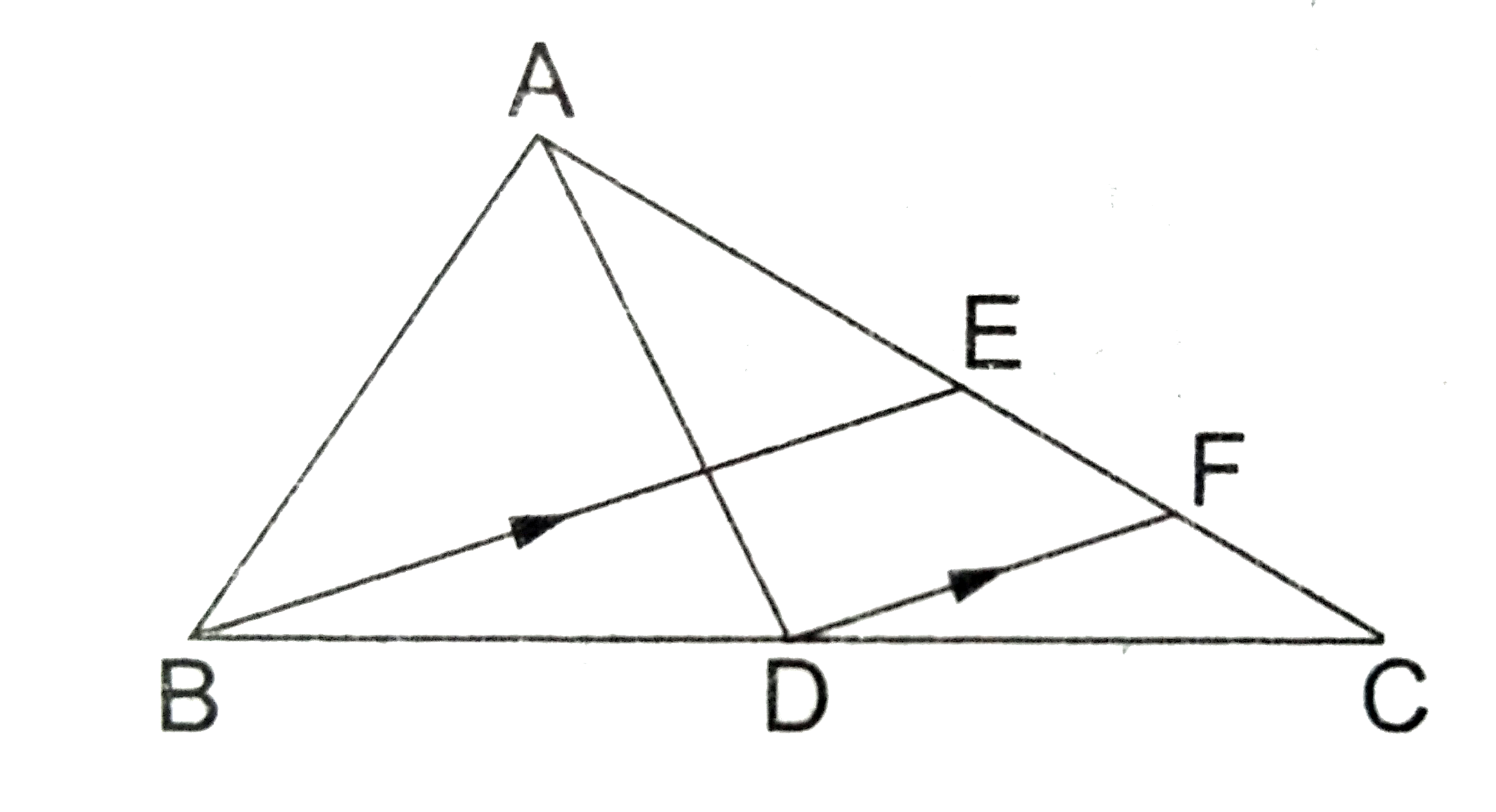
View SolutionIn the adjoining figure, AD and BE are the medians of `triangle ABC` and DF||BE. Show that `CF=(1)/(4)AC.`
View SolutionShow that the diagonals of a parallelogram divide it into four triangles of equal area.
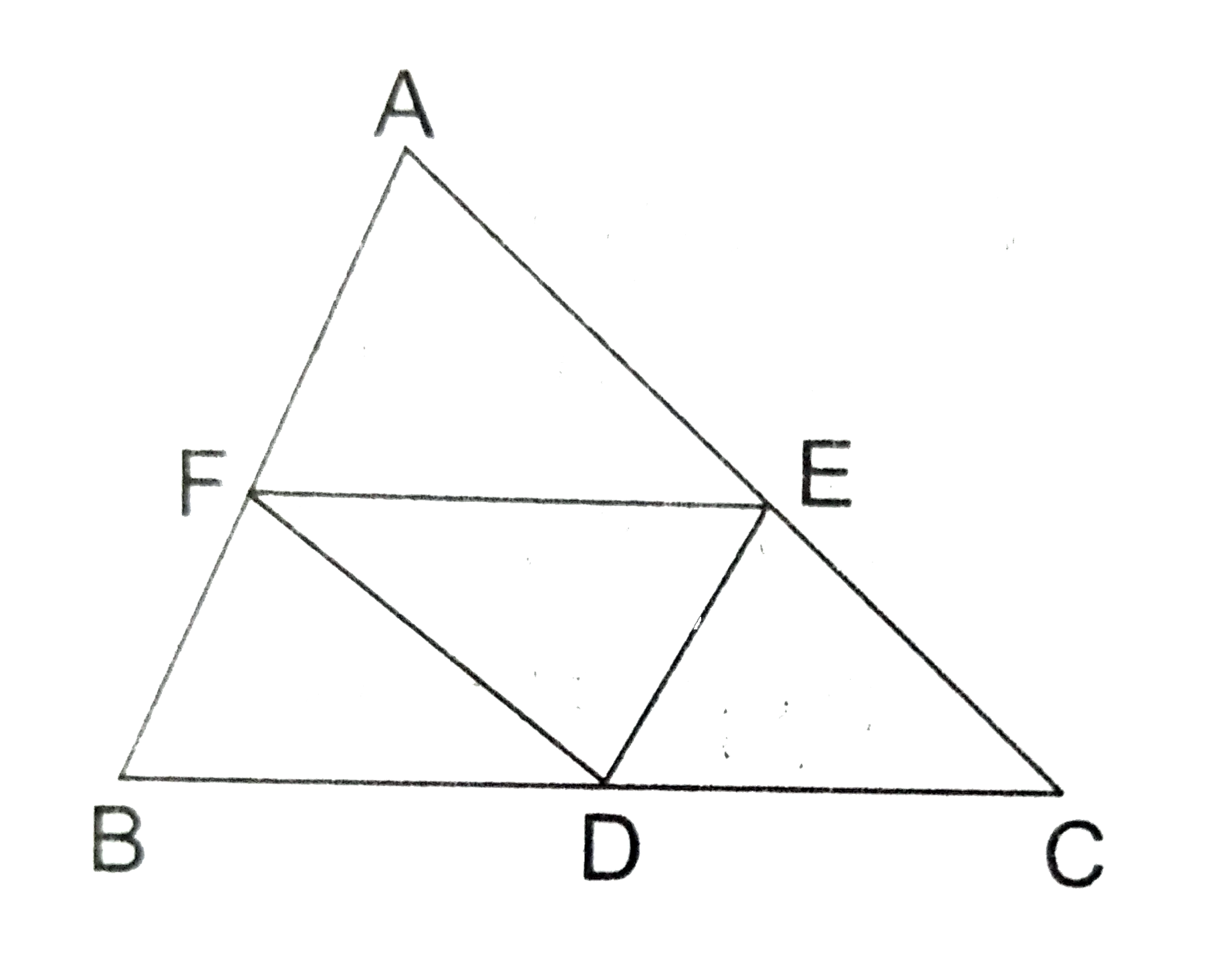
View SolutionIn the adjoining figure, D, E, F are the midpoints of the sides BC, CA and AB respectively, of `triangle ABC.` Show that `angle EDF = angle A, angle DEF= angle B and angle DFE= angle C.`
View SolutionShow that the quadrilateral formed by joining the mid-points of the consecutive sides of a rectangle is a rhombus.
View Solutionprove using vectors: The quadrilateral obtained by joining mid-points of adjacent sides a rectangle is a rhombus.
View SolutionShow that the quadrilateral, formed by joining the mid-points of the sides of a square, is also a square.
View SolutionShow that the line segments joining the mid-points of the opposite sides of a quadrilateral bisect each other
View SolutionThe diagonals of a quadrilateral ABCD are equal. Prove that the quardilateral formed by joining the midpoints of its sides is a rhombus.
View SolutionThe diagonals of a quadrilateral `A B C D` are perpendicular. Show that the quadrilateral, formed by joining the mid-points of its sides, is a rectangle.
View SolutionThe midpoints of the sides `AB, BC, CD and DA` of a quadrilateral ABCD are joined to form a quadrilateral. If `AC = BD and AC _|_ BD` then prove that the quadrilateral formed is a square.
View Solution
EXERCISE 10C questions and complete solutions for chapter QUADRILATERALS of RS AGGARWAL MATHS (HINGLISH) of Class 9