Complete Solutions to EXAMPLE of chapter QUADRILATERALS of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | QUADRILATERALS |
| RS AGGARWAL | EXAMPLE |
| Number Of Questions | 32 |
| Academic Year | 2023-24 |
The sides BA and DC of a quadrilateral are produced as shown in the given figure. Prove that `x+y=a+b.`
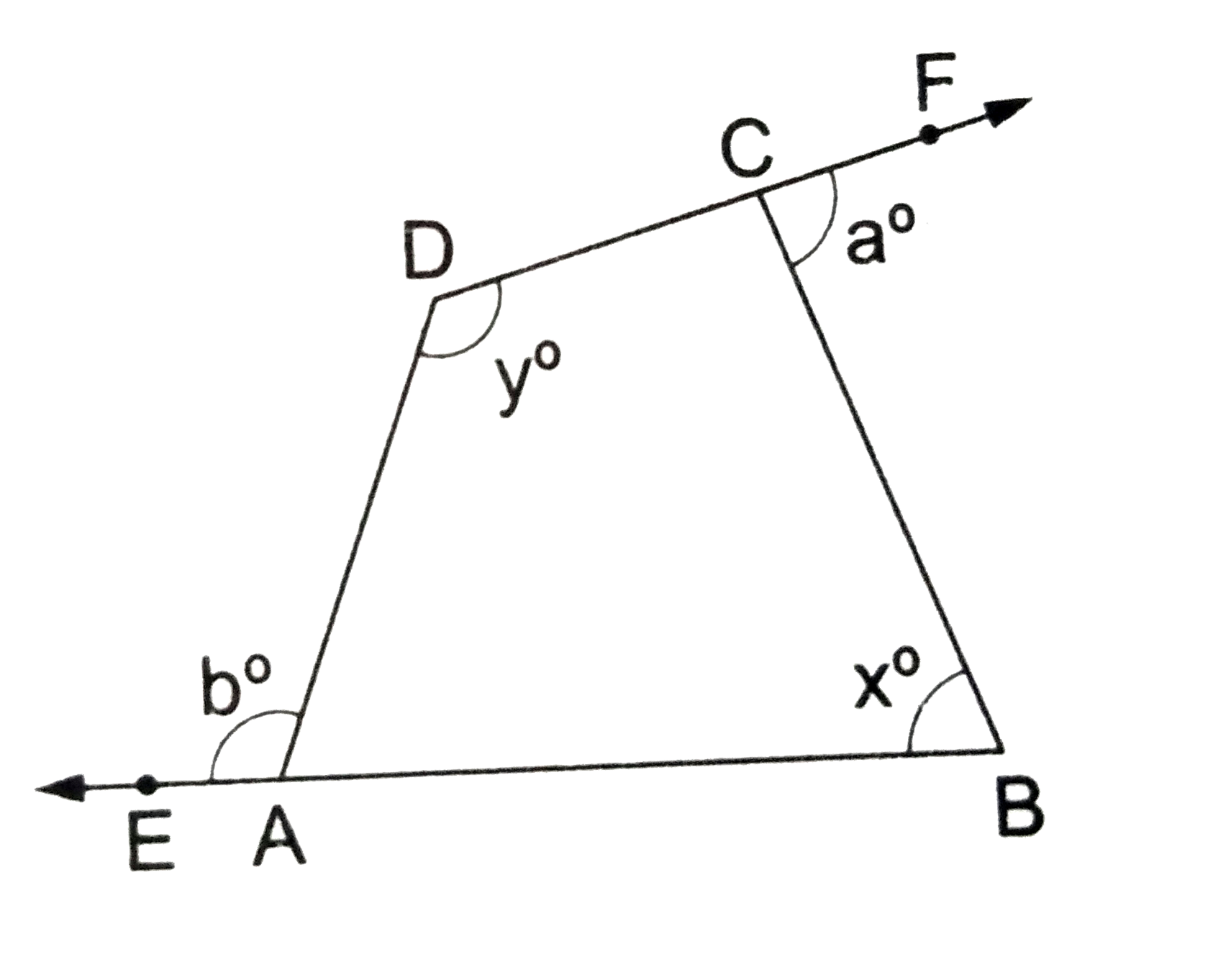
View SolutionIn a quadrilateral ABCD the linesegment bisecting `angleC and angleD` meet at E. Prove that `angleA+angleB=2angleCED.`
View SolutionIn the adjoining figure, a point O is taken inside an equilateral quad. ABCD such that OB = OD. Show that A, O and C are in the same straight line.
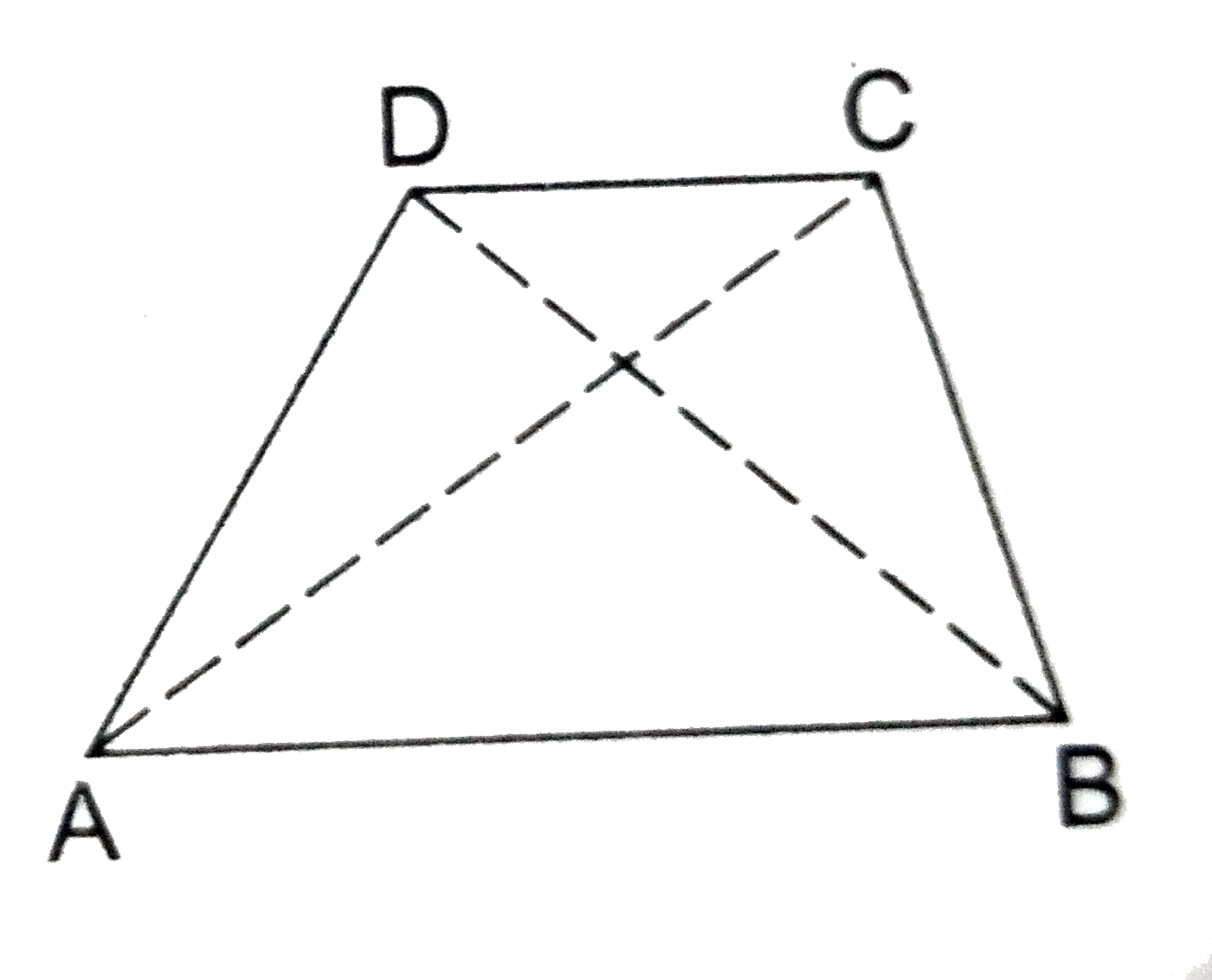
View SolutionIn the adjoining figure, ABCD is a quadrilateral in which AB is the longest side and CD is the shortest side.
Prove that (i) `angle C gt angle A, " (ii) "angle D gt angle B.`
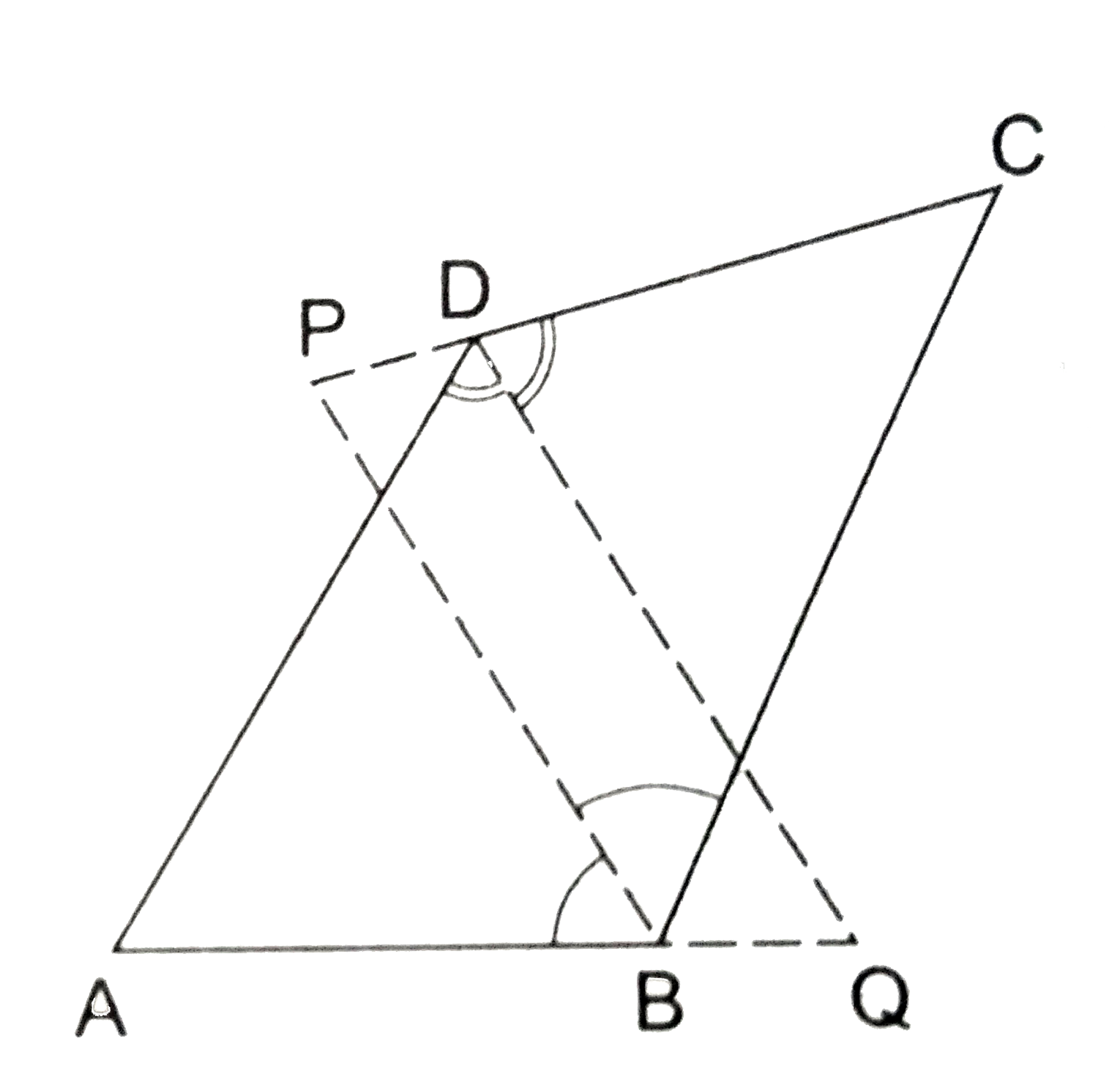
View SolutionIn the adjoining figure, the bisectors of `angle B and angle D ` of a quadrilateral ABCD meet CD and AB produced at P and Q respectively.
Proove that
`angle P + angle Q =(1)/(2) (angle B +angle D).`
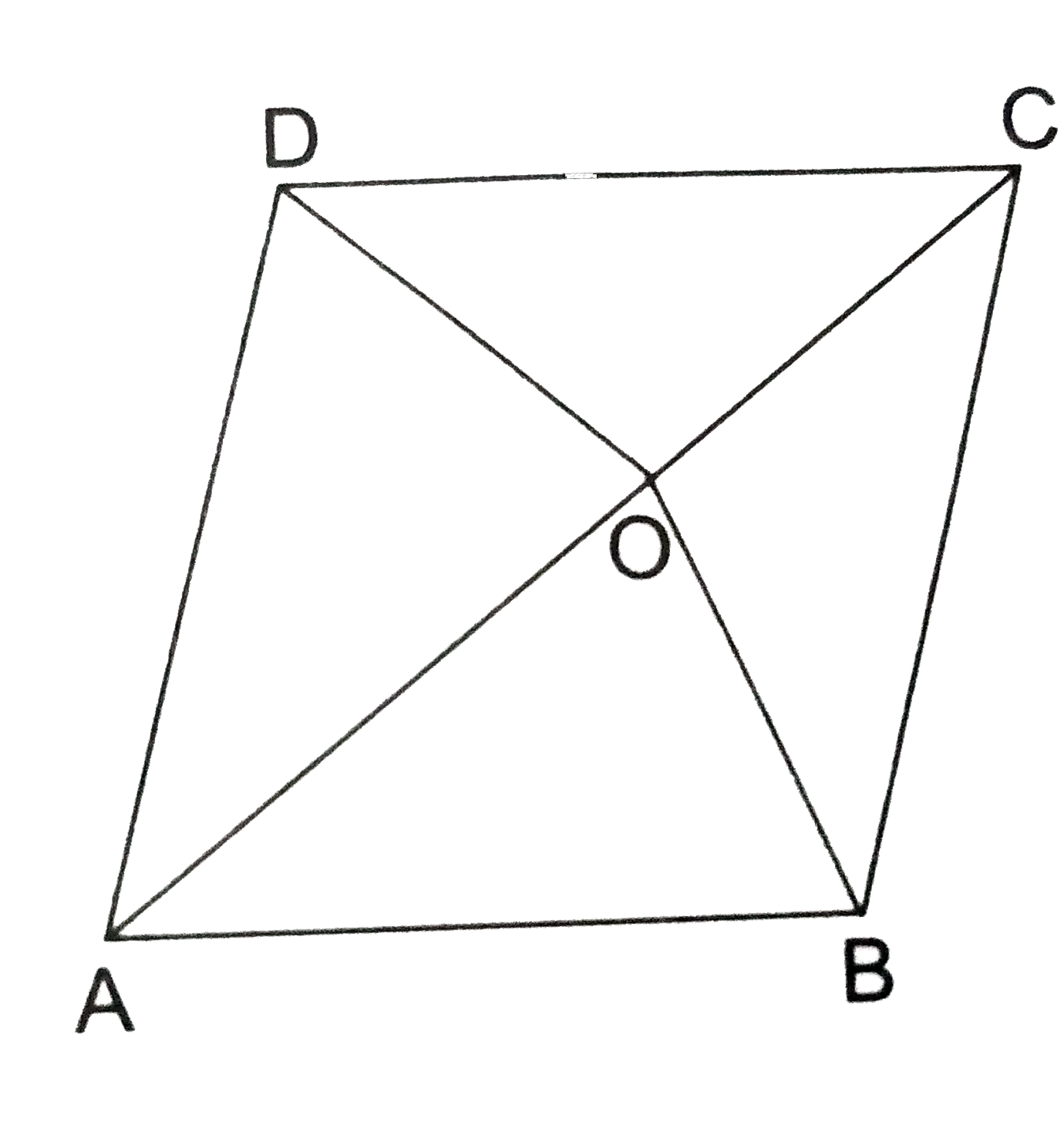
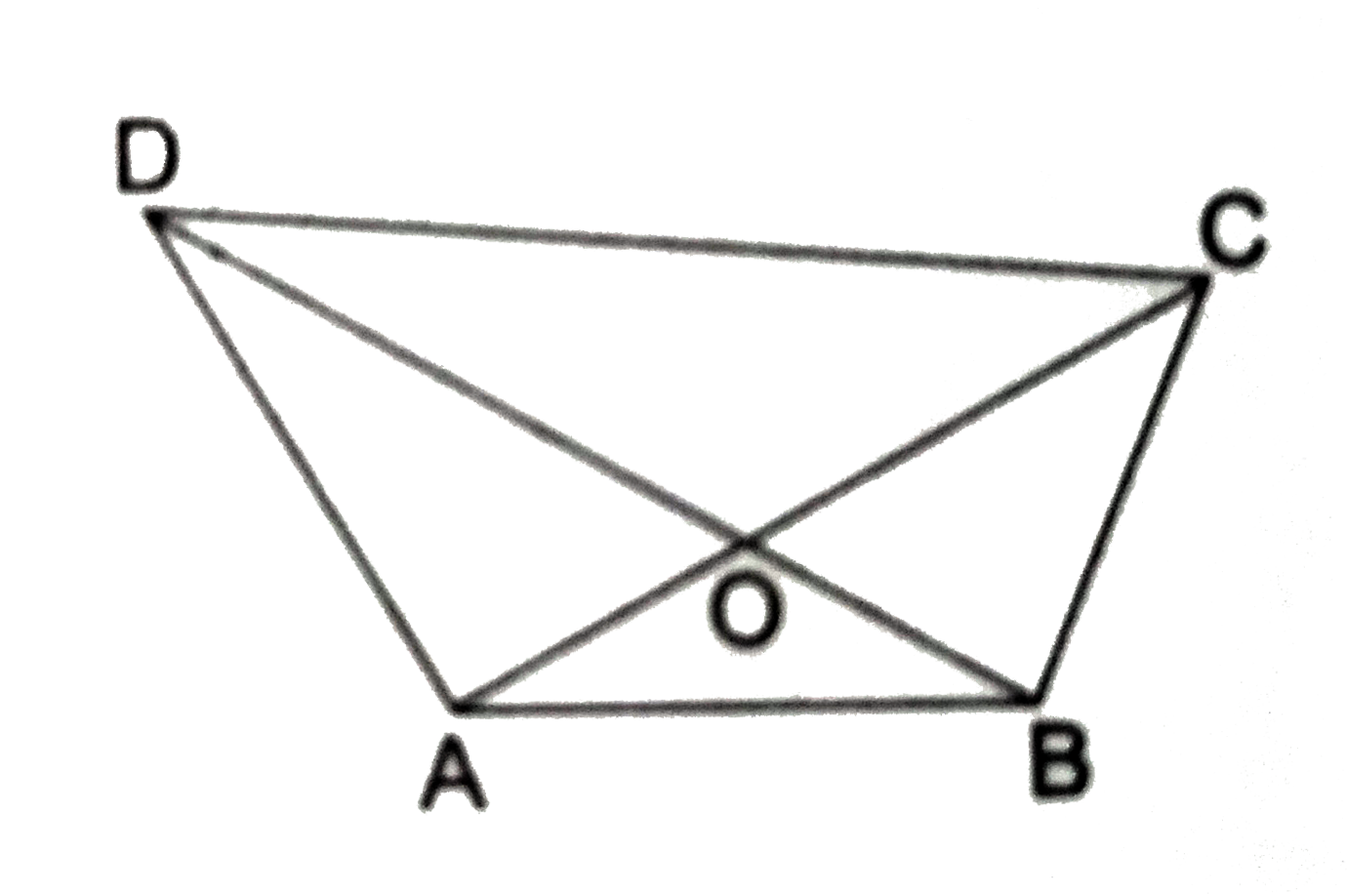
View SolutionIf ABCD is a quadrilateral whose diagonals AC and BD intersect at O, prove that
(i) `(AB + BC + CD +DA) gt (AC + BD),`
(ii) `(AB + BC + CD + DA) lt 2(AC + BD).`
View SolutionIn the given figure, ABCD is a square. A line segment DX cuts the side BC at X and the diagonal AC at O such that `angle COD = 105^(@) and angle OXC = x`. The value of x is

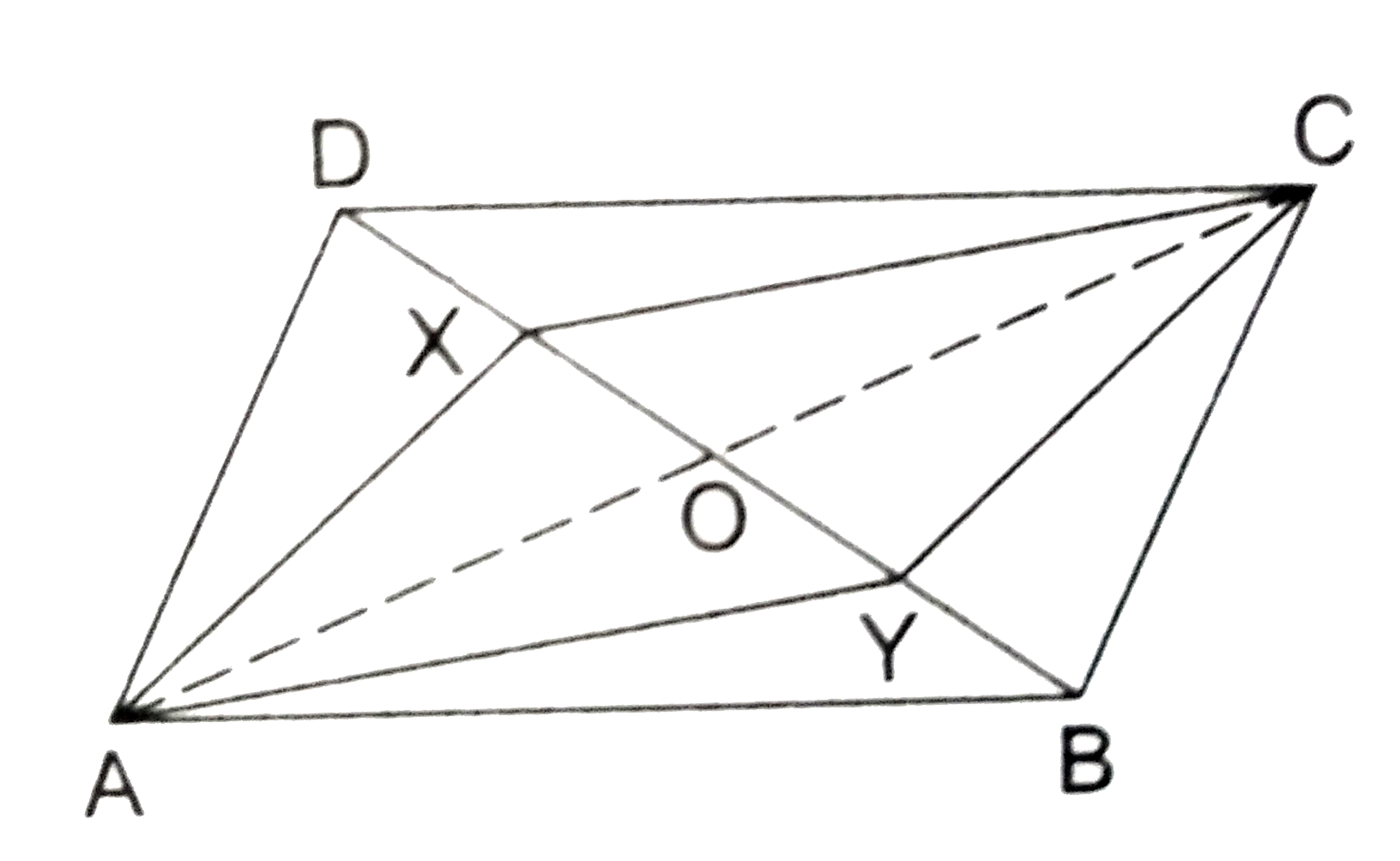
View SolutionIn the adjoining figure, ABCD is a parallelogram and X, Y are the points on the diagonal BD such that DX = BY. Prove that
(i) CXAY is a parallelogram,
(ii) `triangle ADX ~= triangle CBY and triangle ABY ~= triangle CDX, and `
(iii) `AX = CY and CX = AY.`
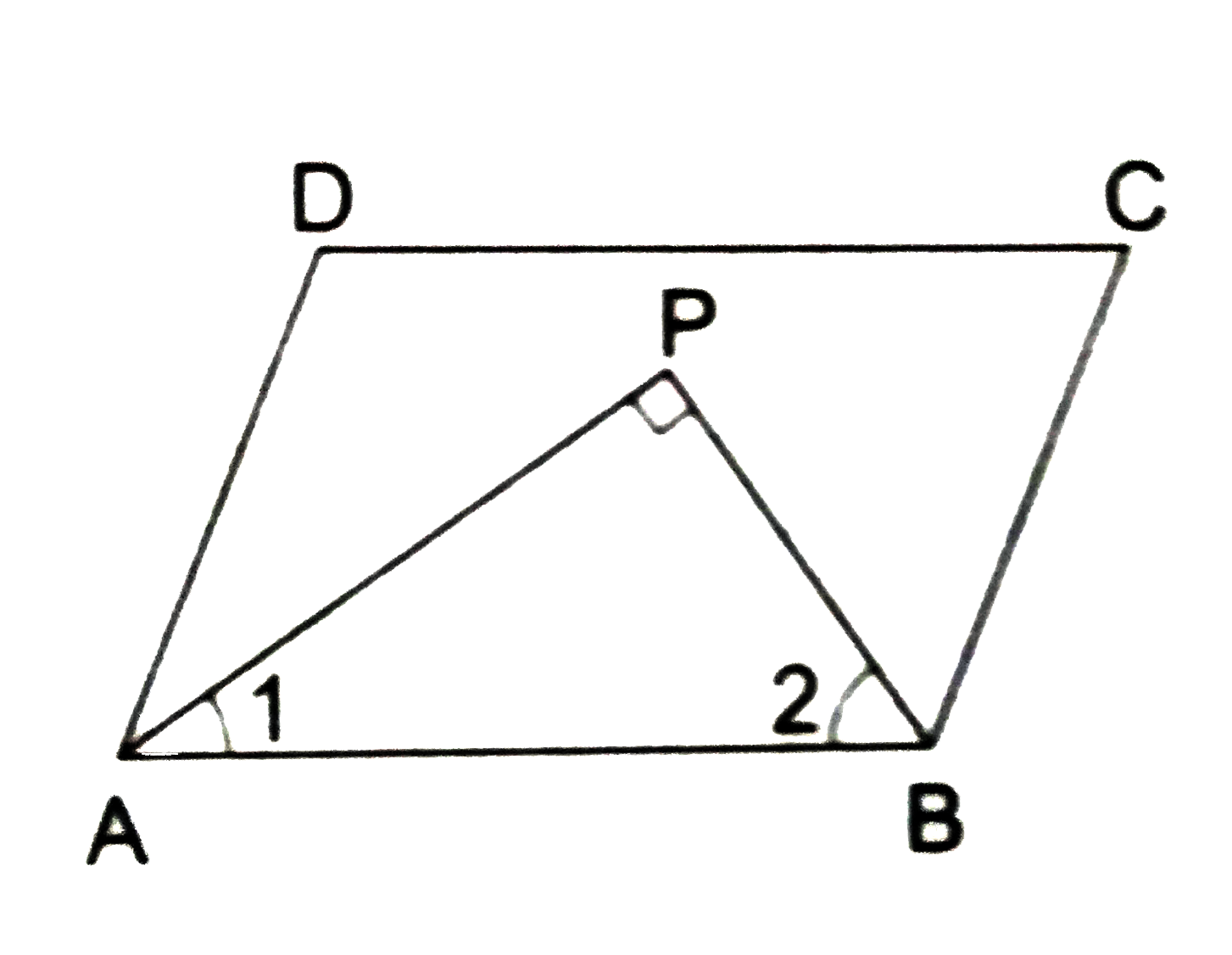
View SolutionProve that in a parallelogram, the bisectors of any two consecutive angles intersect at right angles.
View SolutionABCD is a parallelogram and AL and CM are perpendicualrs from vertices A and C on diagonal BD, as shown in the adjoining figure. Show that (i) `triangle ALB ~= triangle CMD` and (ii) AL = CM.

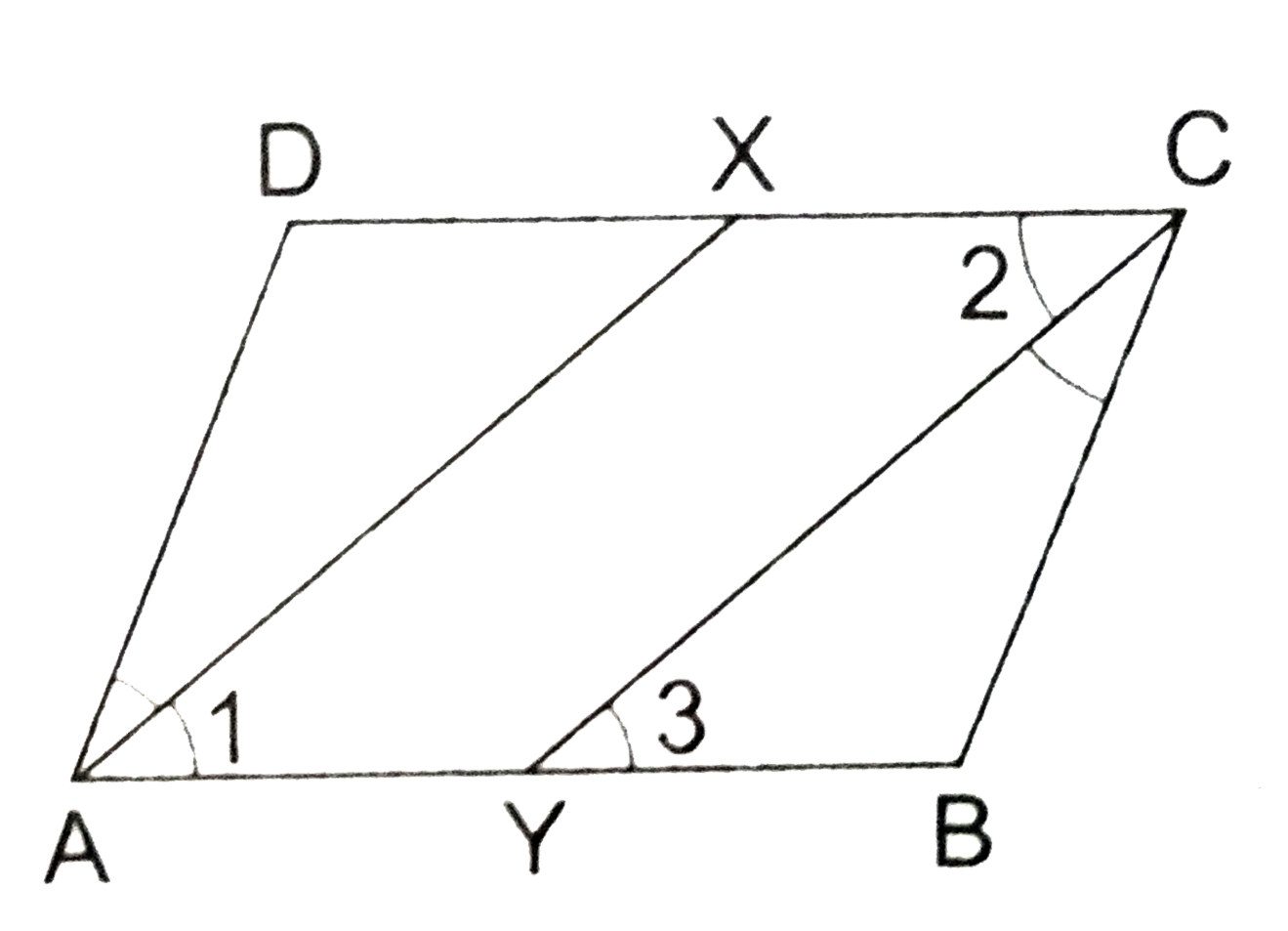
View SolutionIn the adjoining figure, ABCD is a parallelogram and line segments AX and CY bisect `angle A and angle C ` respectively. Proove that AX||CY.
View SolutionShow that the bisectors of the angles of a parallelogram enclose a rectangle.
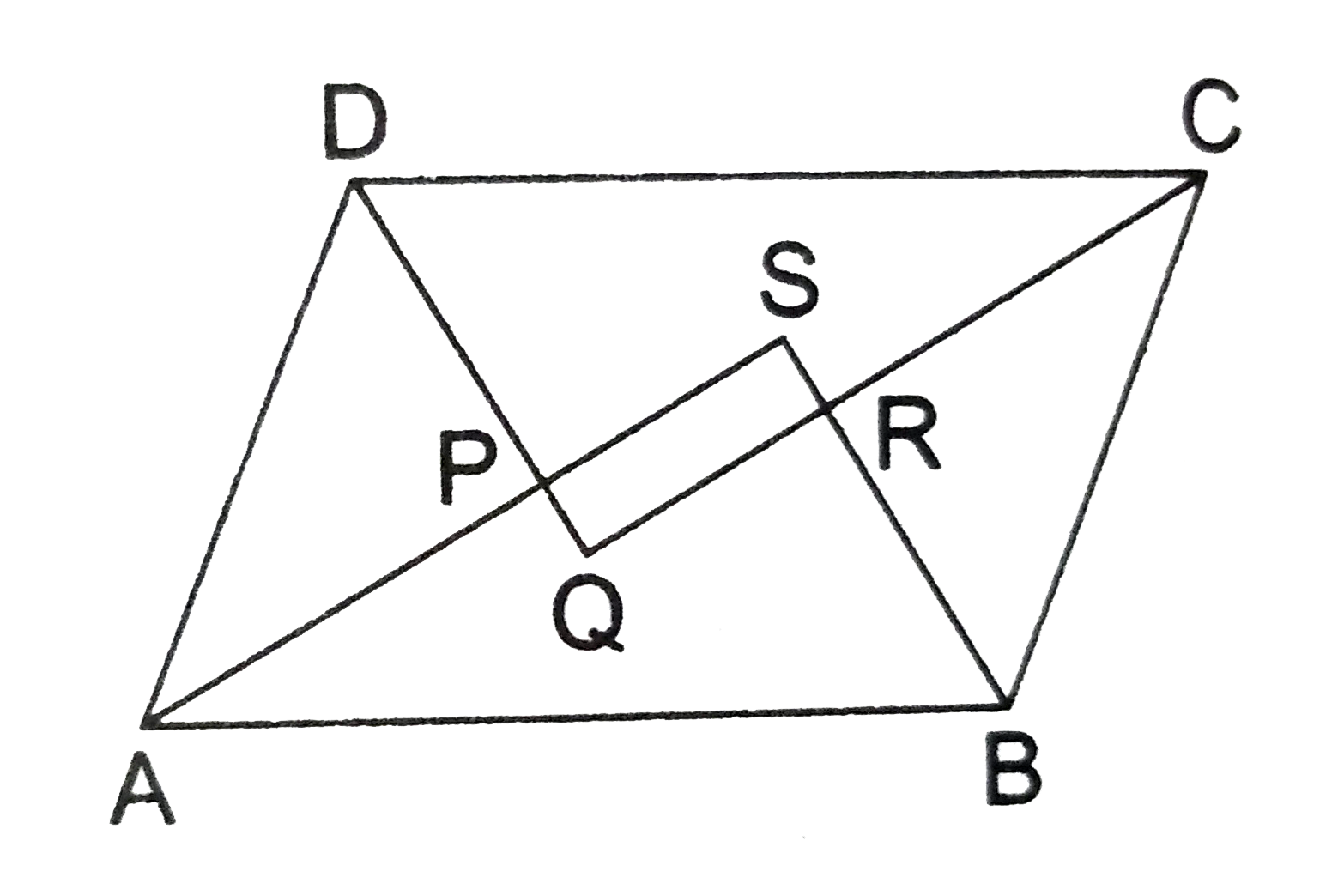
View SolutionIf a diagonal of a parallelogram bisects one of the angles of the parallelogram, prove that it also bisects the angle opposite it, and that the two diagonals are perpendicular to each other.
Also, prove that it is a rhombus.
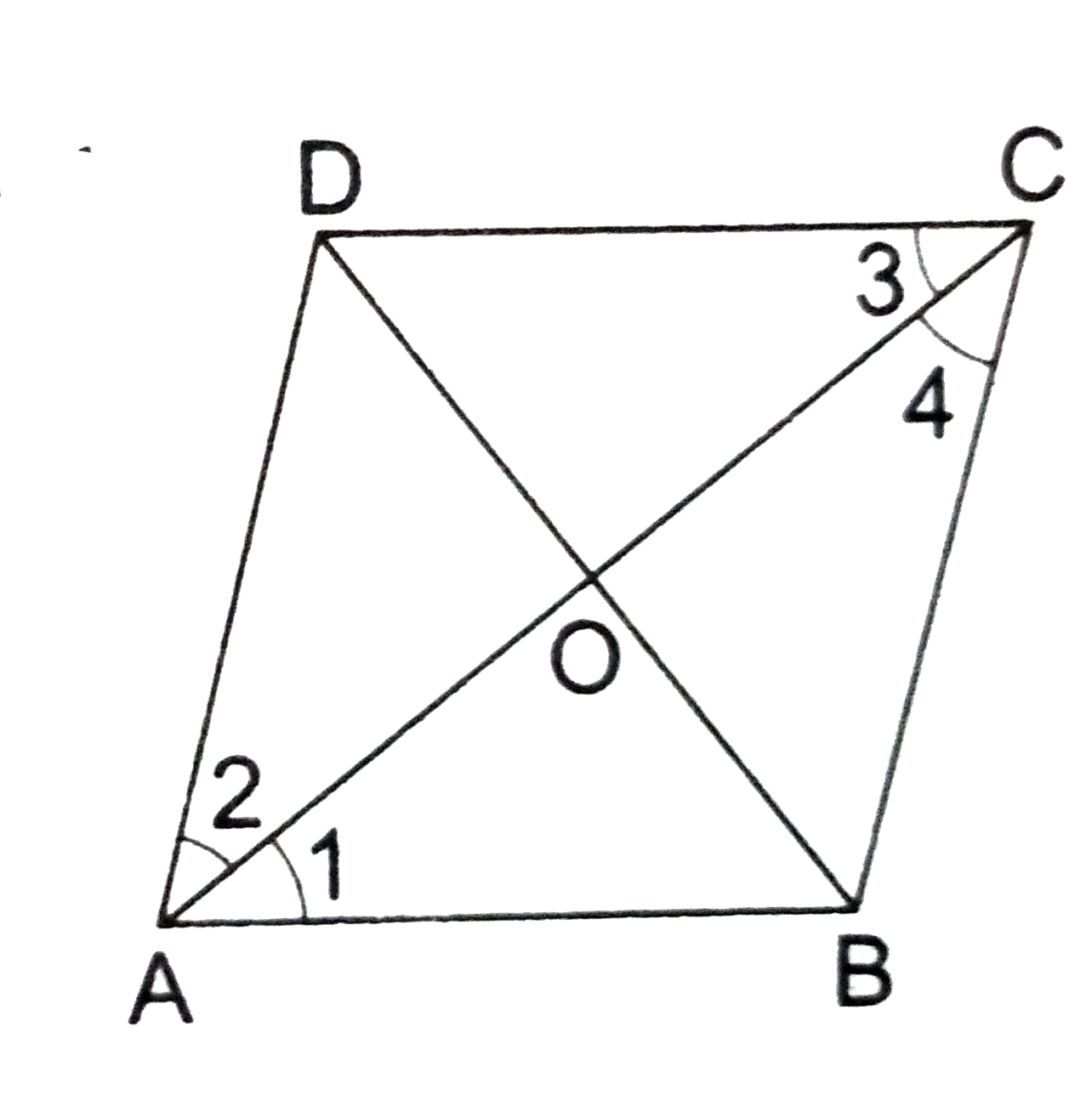
View SolutionLet `triangle ABC and triangle DEF` be two triangles given in such a way that AB||DE, AB = DE, BC||EF and BC = EF.
Prove that
(i) AC||DF and AC = DF,
(ii) `triangle ABC ~= triangle DEF.`

View SolutionIn the adjoining figure, ABCD is a parallelogram in which X and Y are the midpoints of AB and DC respectively. If AY and DX intersect in P while CX and BY intersect in Q, show that
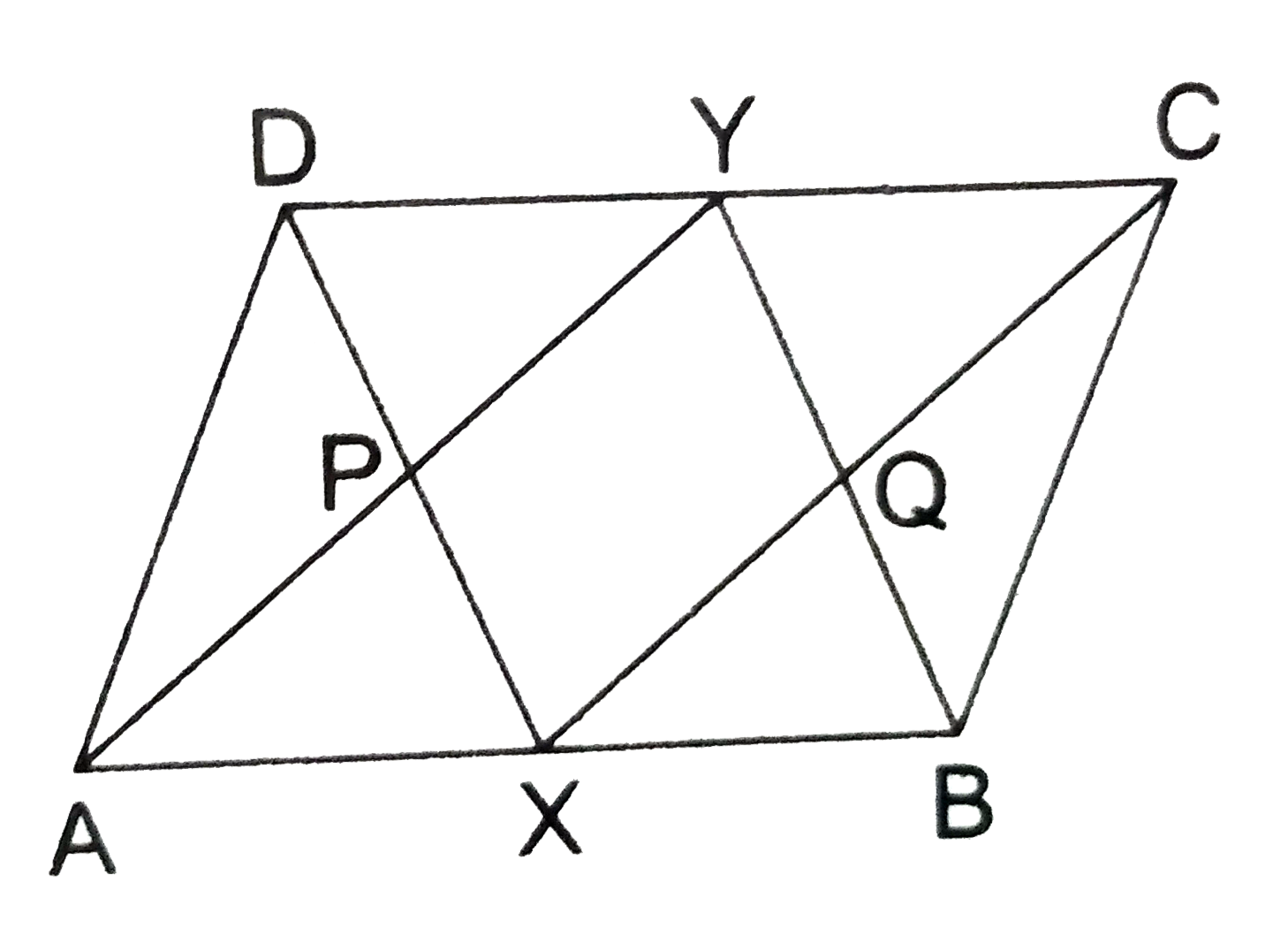
(i) quad. AXCY is a parallelogram,
(ii) quad. XBYD is a parallelogram,
(iii) quad. PXQY is a parallelogram.
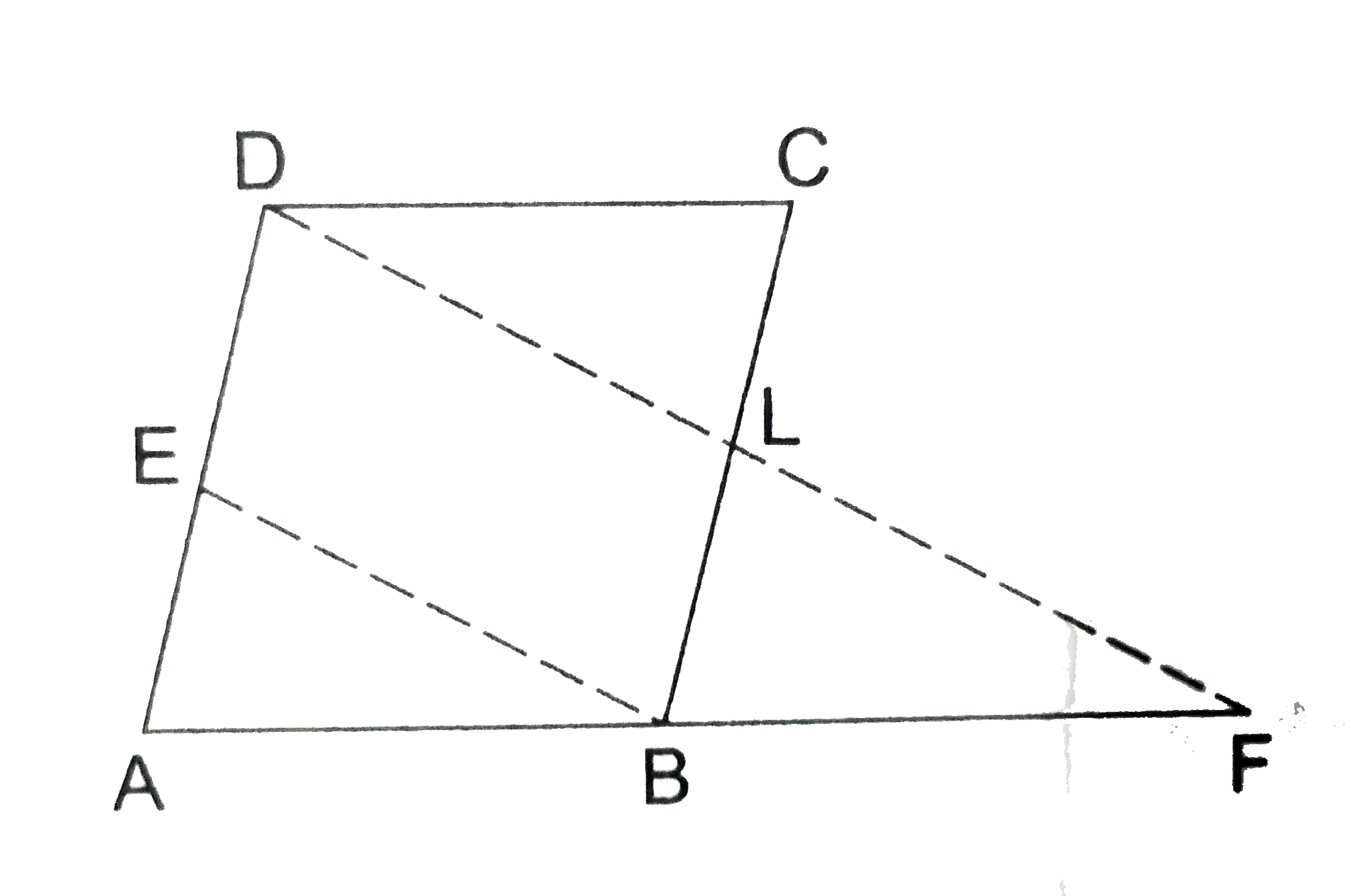
View SolutionIn the adjoining figure, ABCD is a parallelogram and E is the midpoint of AD. A line through D, drawn parallel to EB, meets AB produced at F and BC at L. Prove that
(i) AF = 2 DC and (ii) DF = 2DL.
View SolutionIn the adjoining figure, AB = AC: CP||BA and AP is the bisector of `angle CAD. ` Prove that
(i) `angle PAC = angle BCA and `
(ii) ABCP is a parallelogram.
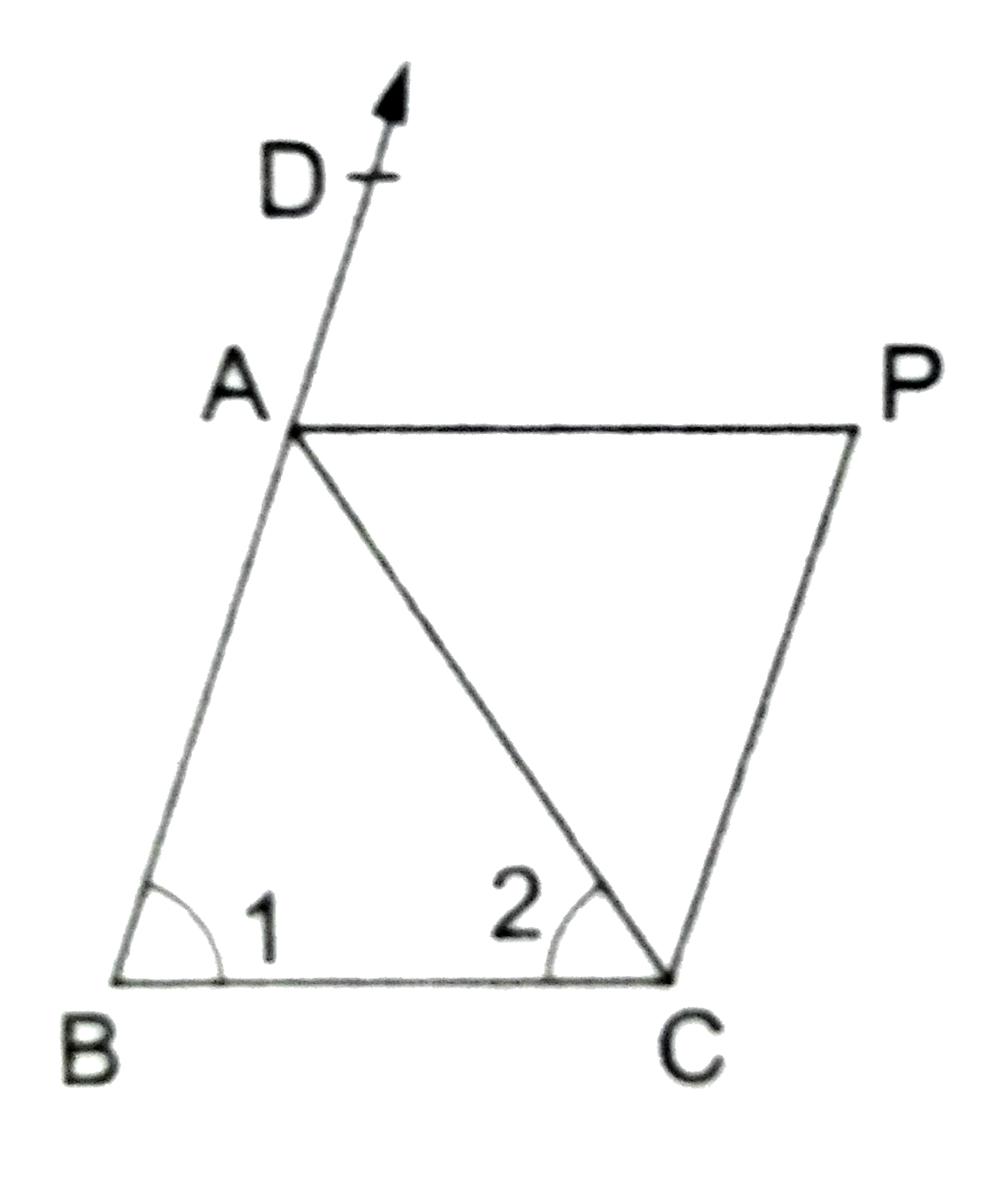
View SolutionIn the adjoining figure, ABCD is a parallelogram and the bisector of `angle A` bisects BC at X. Prove that AD = 2AB.
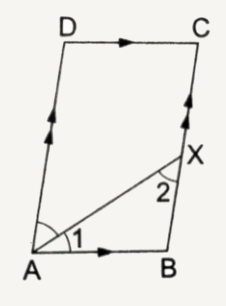
View SolutionIn the adjoining figure, ABCD is a parallelogram, E is midpoint of AB and CE bisects `angle BCD`. Prove that
(i) AE = AD (ii) DE bisects `angle ADC ` and (iii) `angle DEC = 90^(@)`.
View SolutionABCD is a trapezium in which AB||CD and AD = BC. Show that
(i) `angle A = angle B and angle C = angle D , " (ii) " triangle ABC ~= triangle BAD and`
(ii) AC = BD.
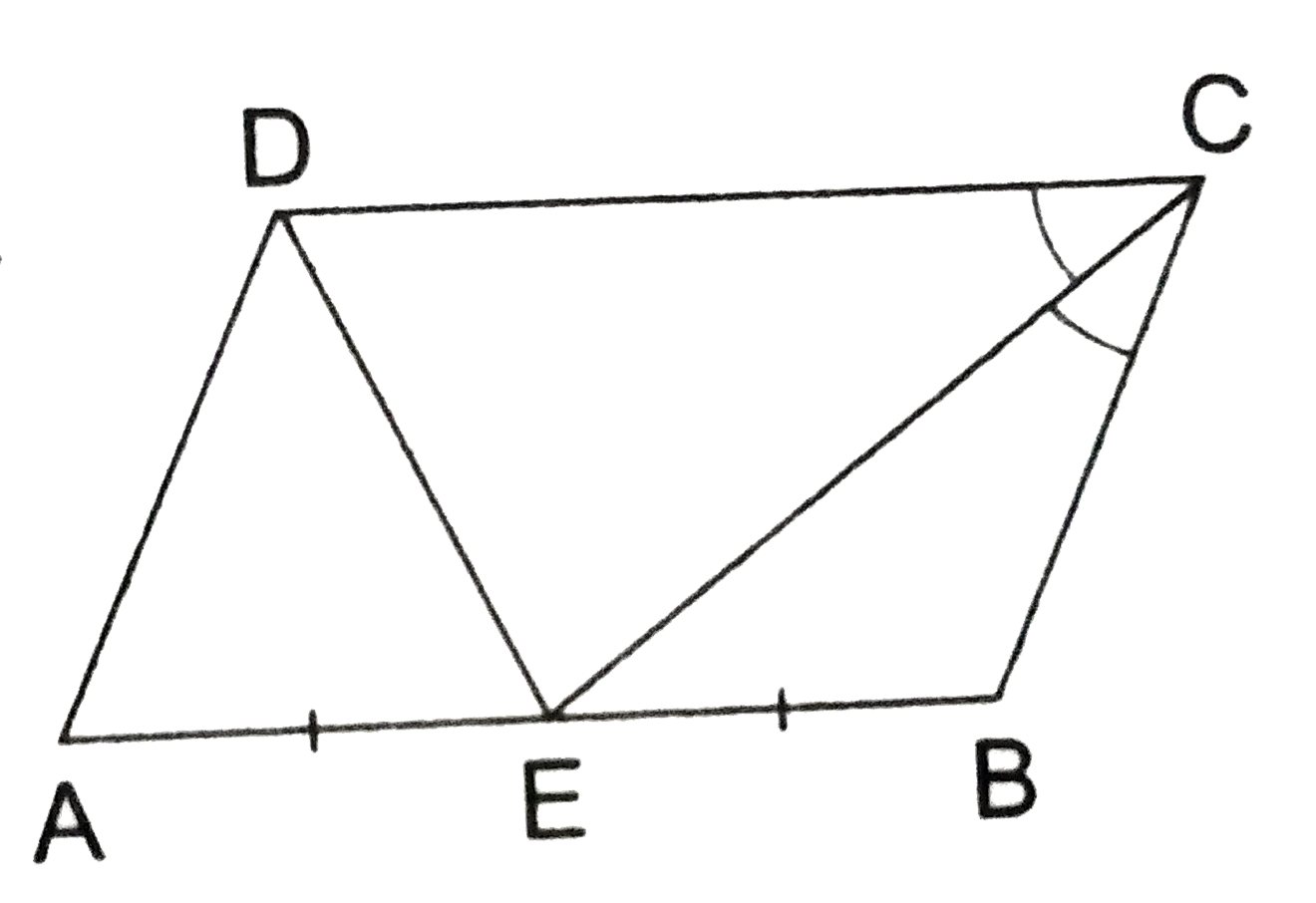
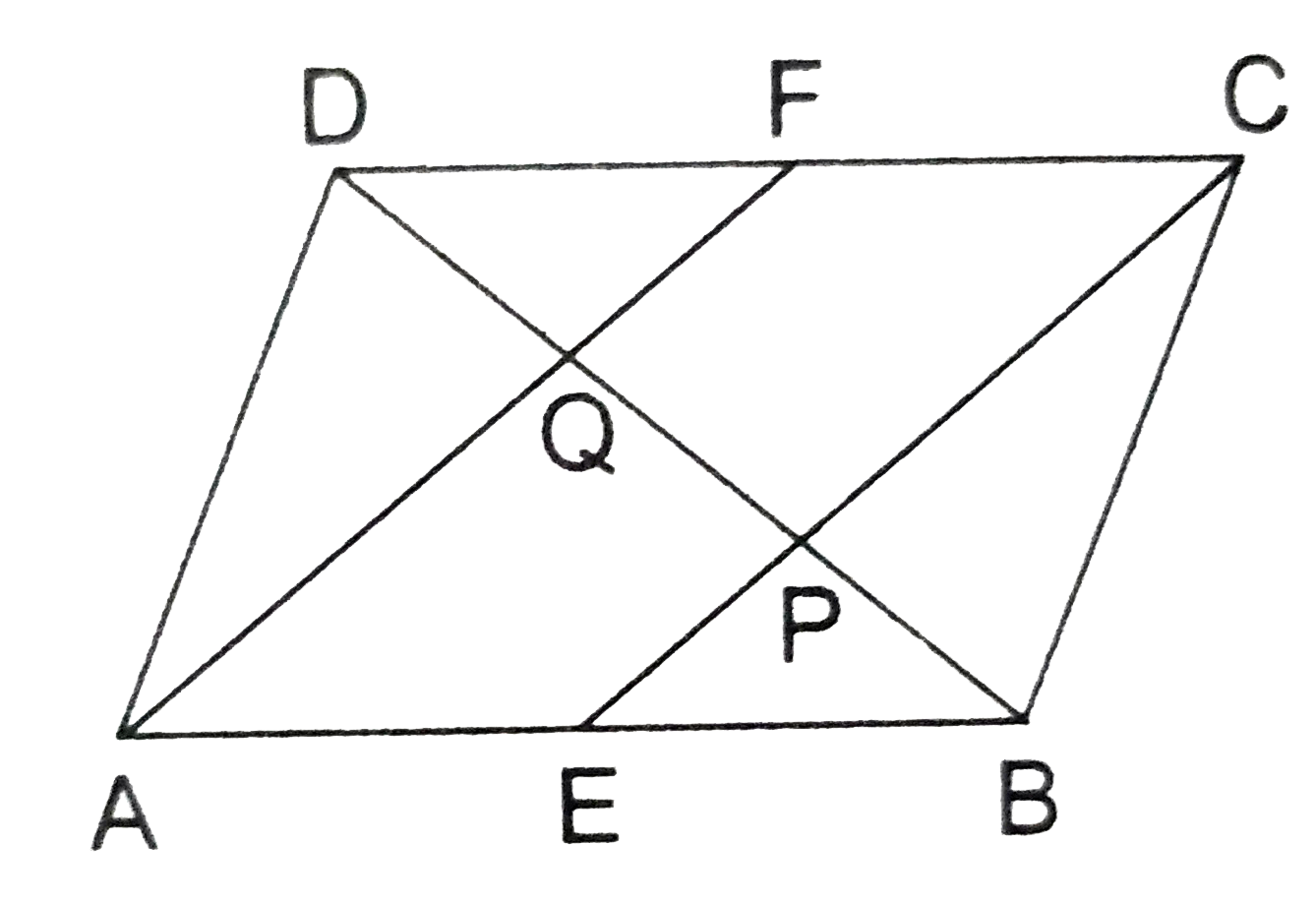
View SolutionABCD is a parallelogram in which E and F are the midpoints of the sides AB and CD respectively. Prove that the line segments CE and AF trisect the diagonal BD.
View SolutionLet ABCD be a trapezium in which AB||DC and let E be the midpoint of AD. Let F be a point on BC such that EF||AB. Prove that
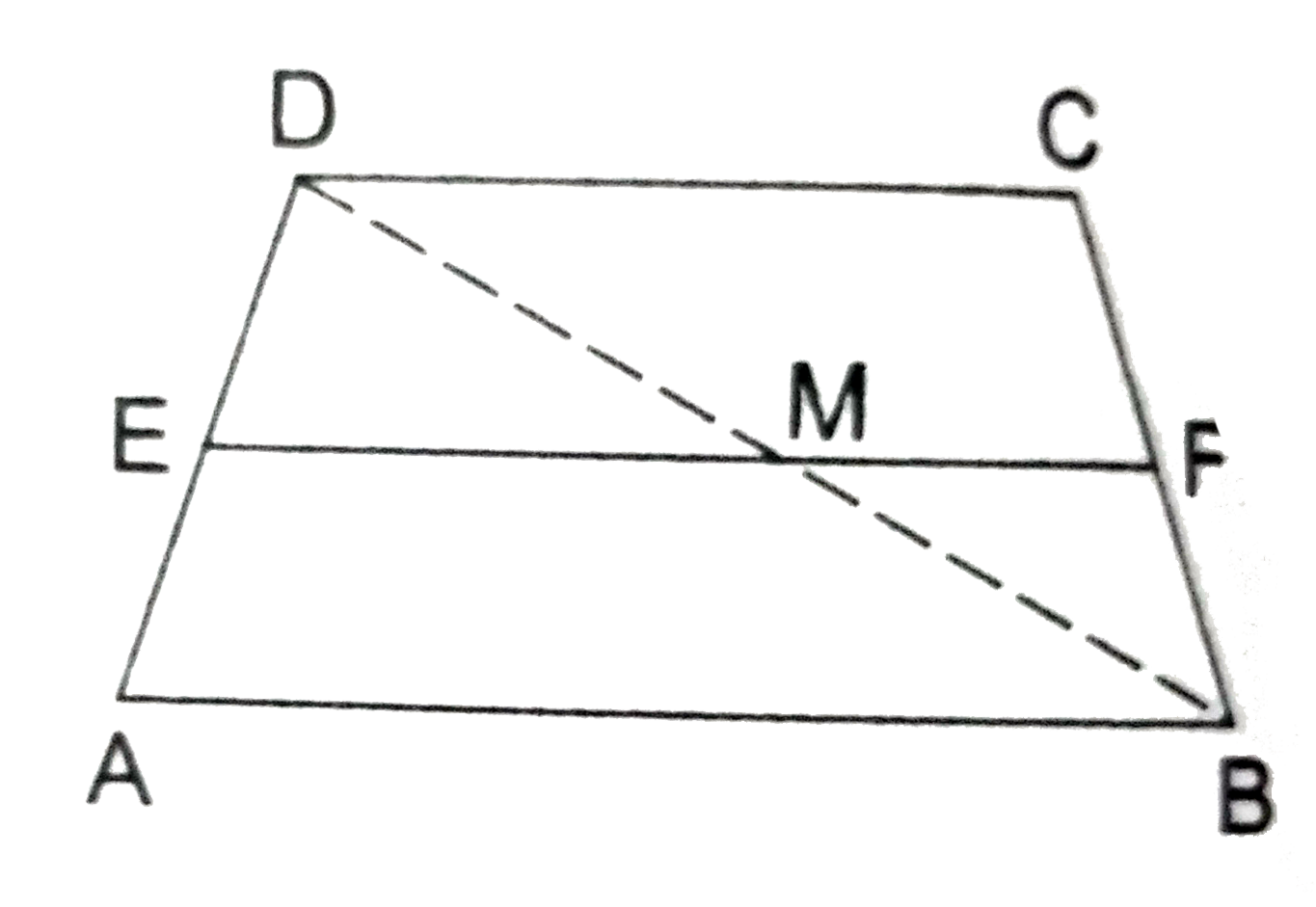
(i) F is the midpoint of BC, (ii) `EF =(1)/(2)(AB+DC).`
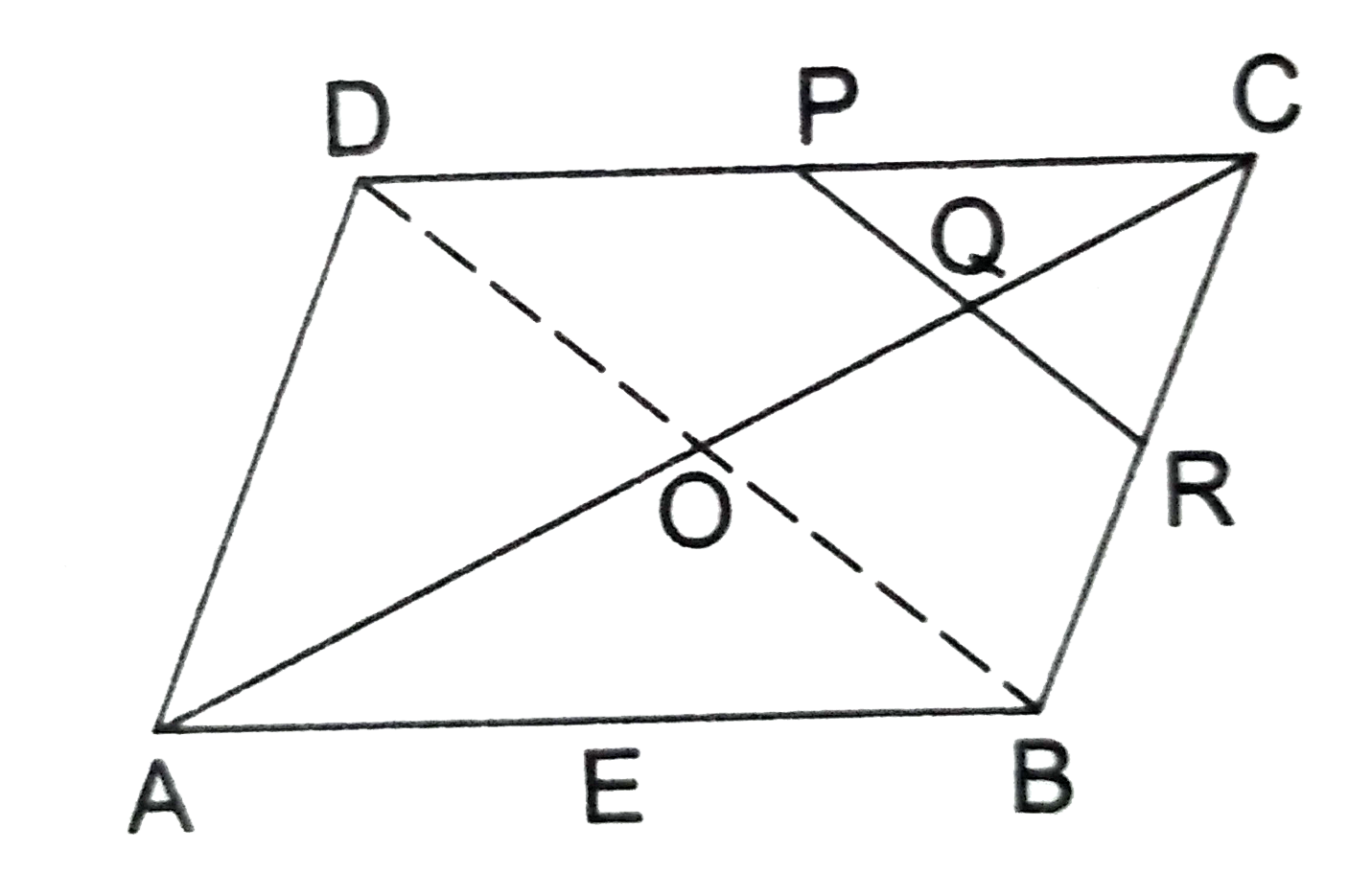
View SolutionIn the adjoining figure, ABCD is a ||gm in which P is the midpoint of DC and Q is a point on AC such that `CQ=(1)/(4)AC.` Also, PQ when produced meets BC at R. Prove that R is the midpoint of BC.
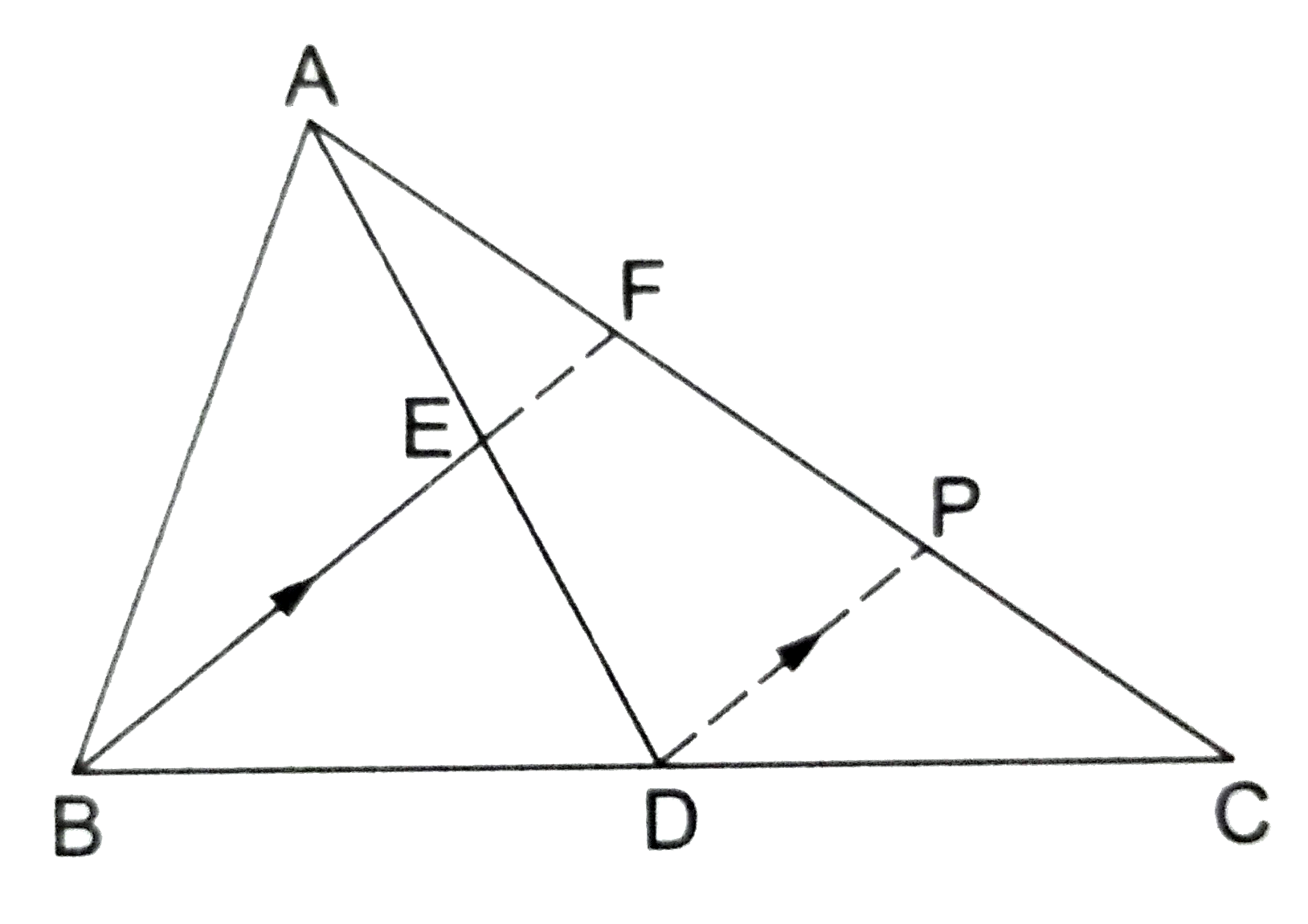
View SolutionIn the adjoining figure, AD is a median of `triangle ABC` and E is the midpoint of AD. Also, BE produced meets AC in F. Prove that `AF=(1)/(3) AC.`
View SolutionIn the adjoining figure, ABCD is a trapezium in which AB||DC and AD = BC. If P, Q, R, S be respectively the midpoints of BA, BD, CD, CA then show that PQRS is a rhombus.

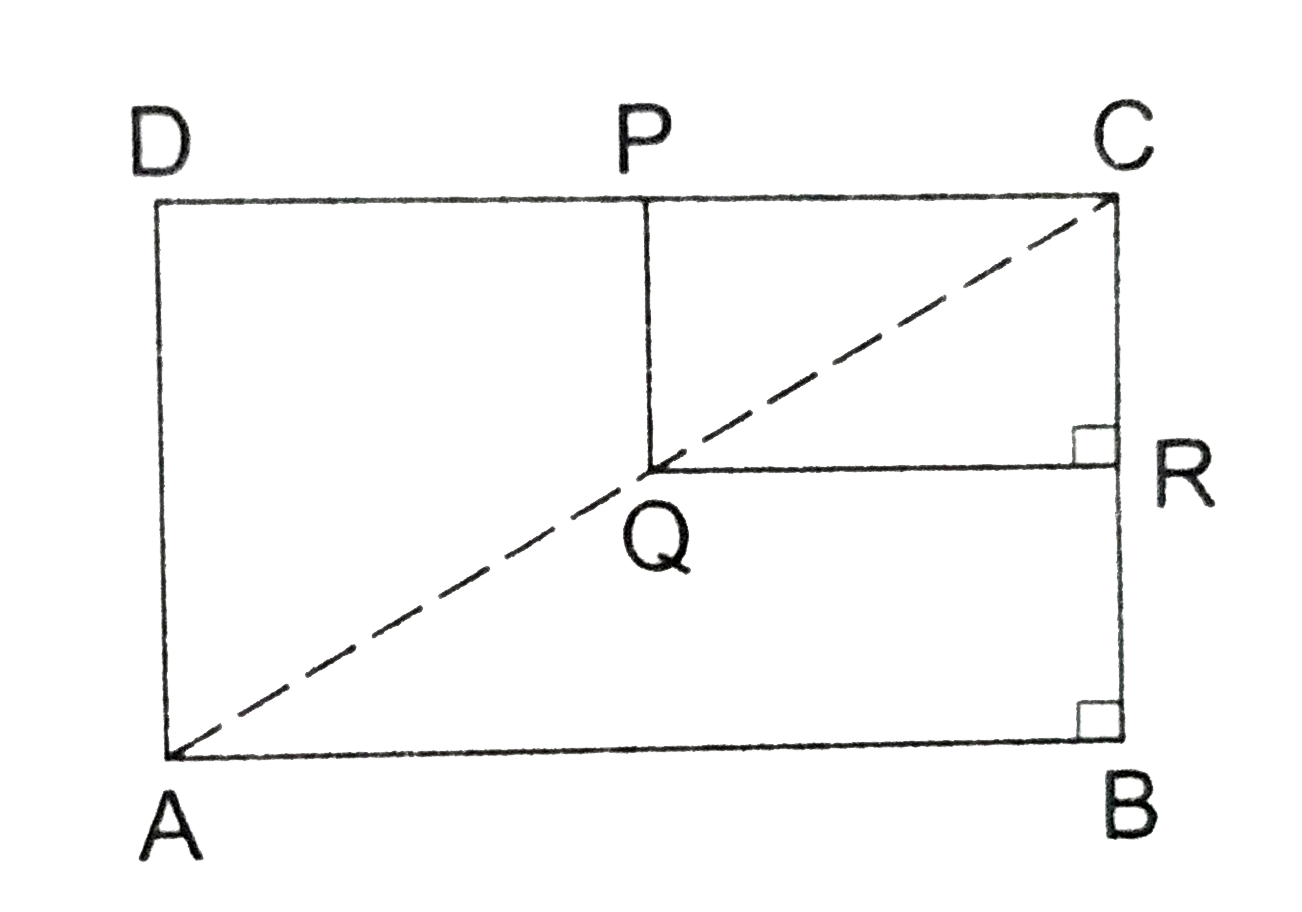
View SolutionIn the adjoining figure, ABCD and PQRC are rectangles, where Q is the midpoint of AC. Prove that
(i) `DP=PC, " (ii) " PR=(1)/(2) AC. `
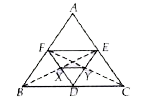
View SolutionIn the given figure, D, E and F are the midpoints of the sides BC, CA and AB of `DeltaABC. BE` bisect DF at X while CF bisect DE at Y, then BC = a XY. Find a.
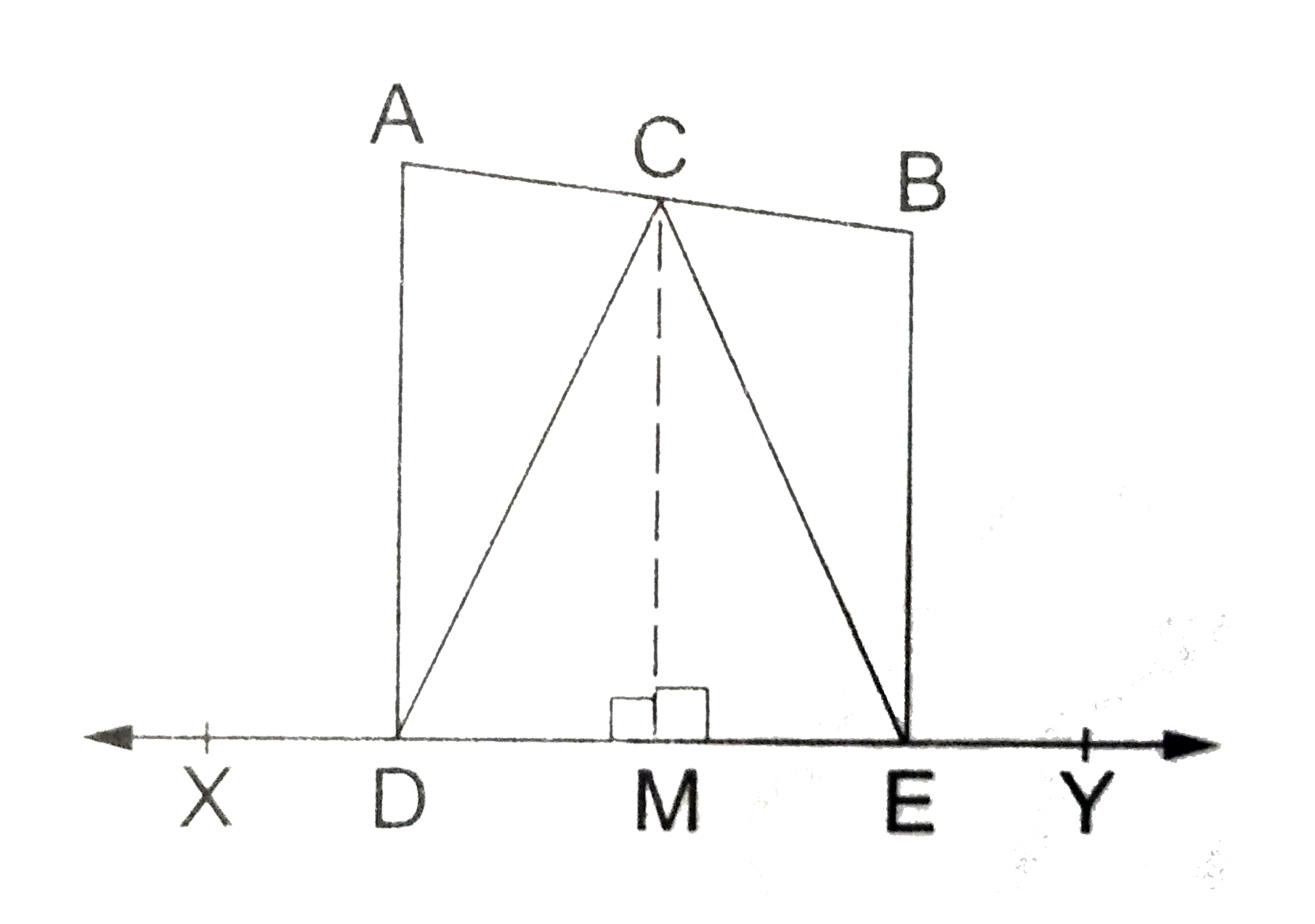
View SolutionIn the adjoining figure, two points A and B lie on the same side of a line XY. If `AD bot XY, BE bot XY` and C is the midpoint of AB, prove that CD = CE.
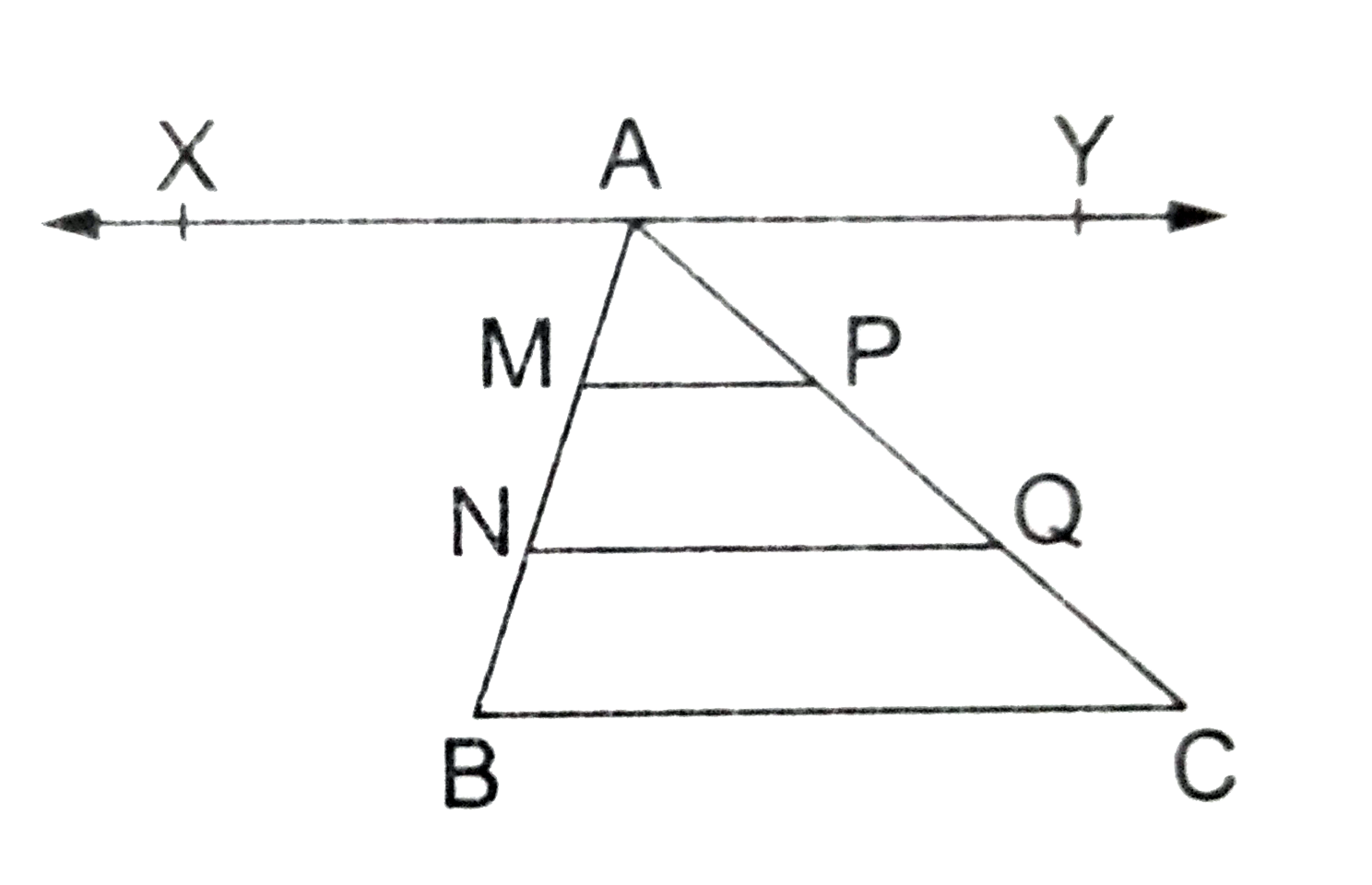
View SolutionIn the adjoining figure, points M and N divide the side AB of `triangle ABC` into three equal parts. Line segments MP and NQ are both parallel to BC and meet AC in P and Q respectively. Prove that P and Q divide AC into three equal parts.
View SolutionE and F are respectively the midpoints of nonparallel sides AD and BC of a trapezium ABCD. Prove that EF||AB.
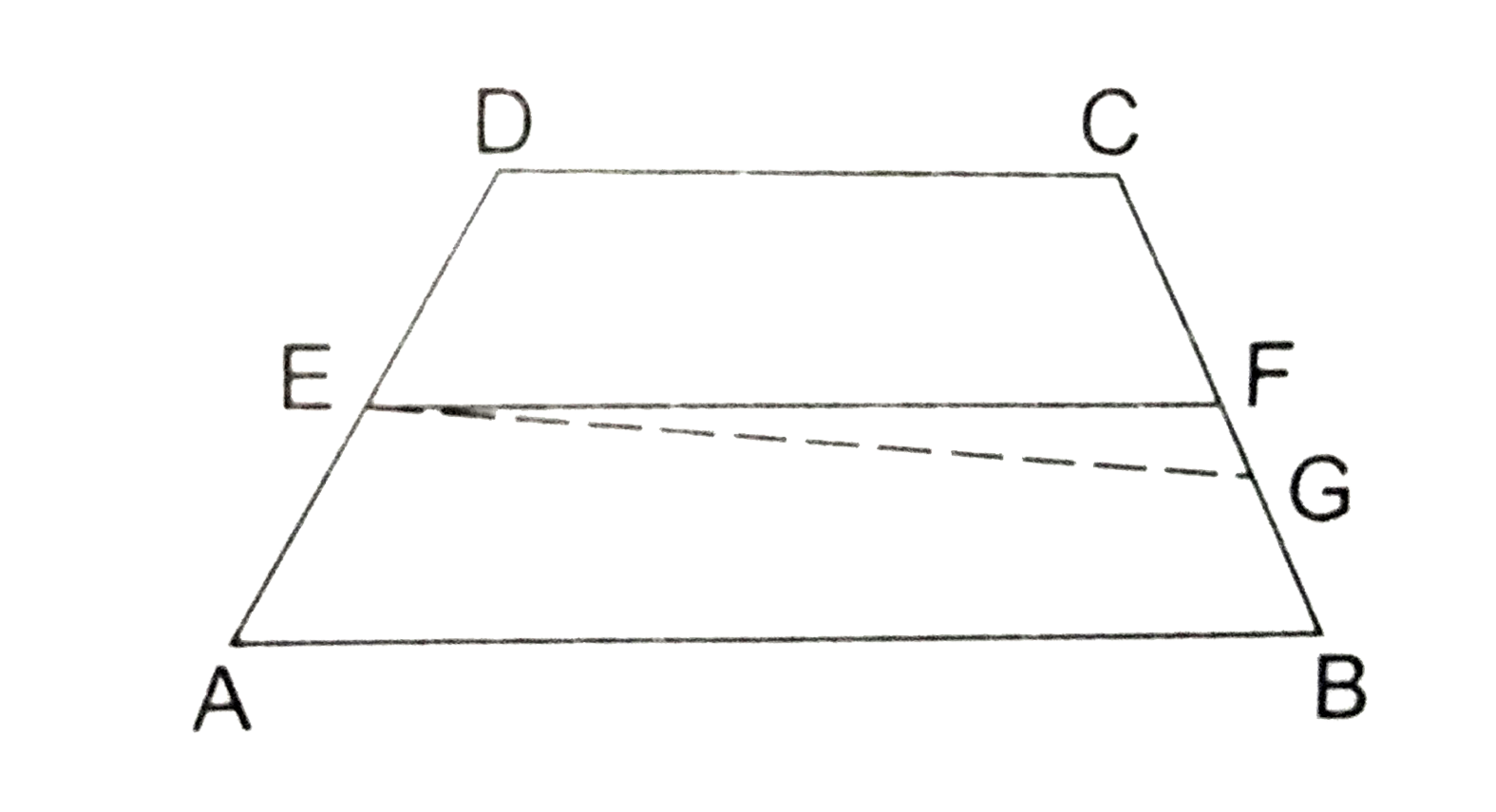
View SolutionProve that any line segment drawn from the vertex of a triangle to the base is bisected by the line segment joining the midpoints of the other sides of the triangle.
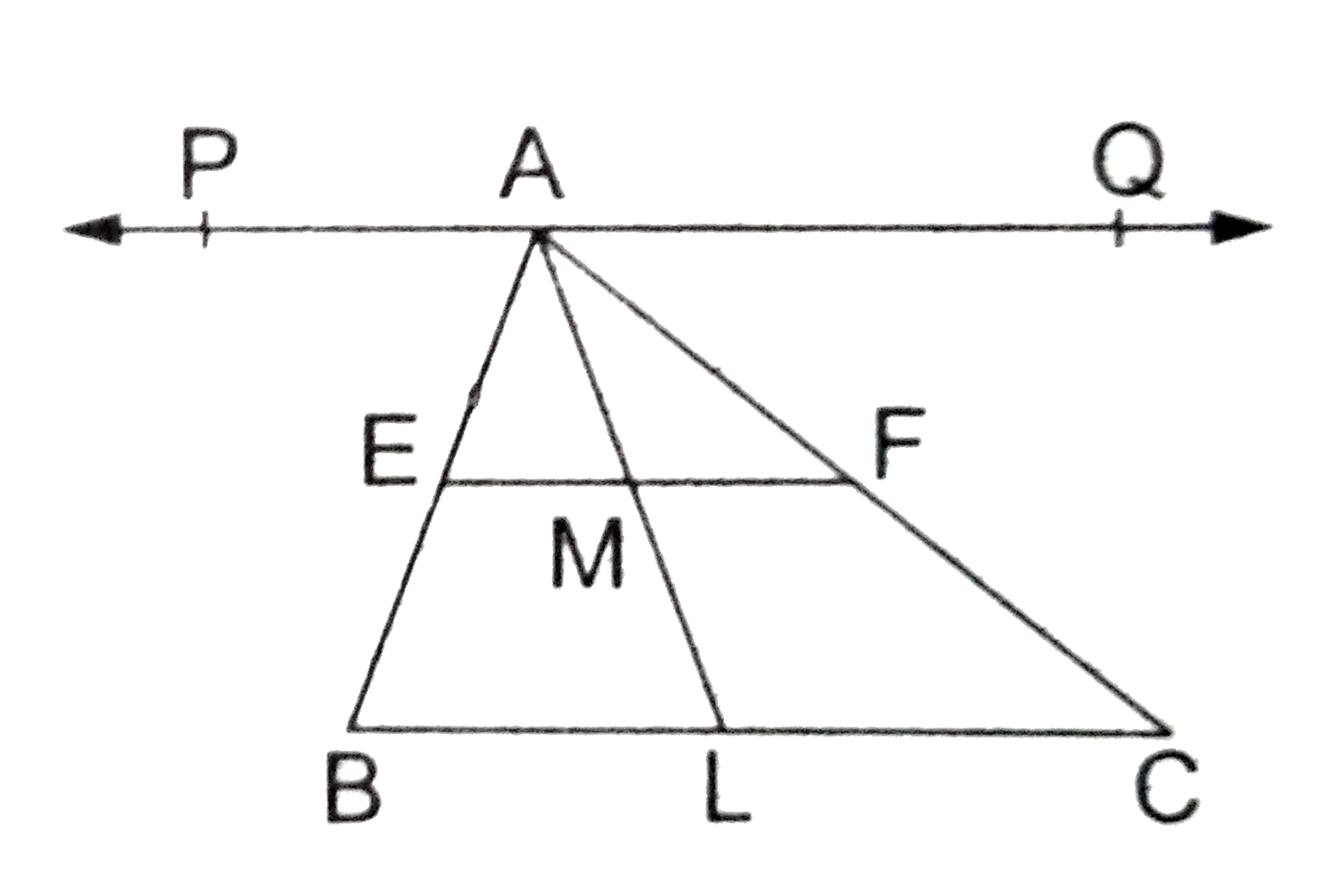
View SolutionIn the adjoining figure, the side AC of `triangle`ABC is produced to E such that `CE=(1)/(2)AC`. If D is the midpoint of BC and ED produced meets AB at F, and CP, DQ are drawn parallel to BA, prove that `FD =(1)/(3)FE.`
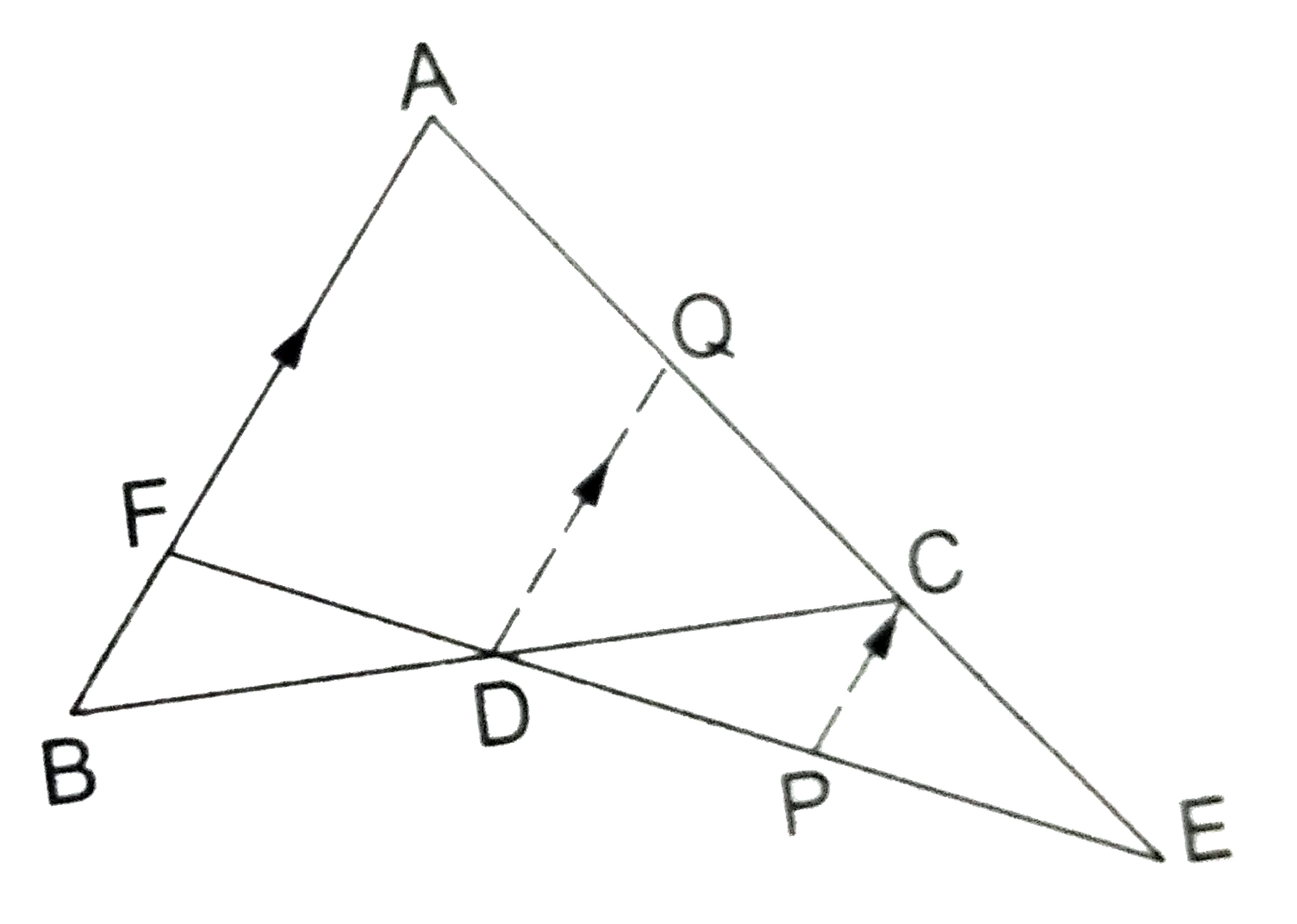
View Solution
EXAMPLE questions and complete solutions for chapter QUADRILATERALS of RS AGGARWAL MATHS (HINGLISH) of Class 9