Level 1 from ARIHANT PHYSICS Chapter 8 KINEMATICS for Class 11
| Class 11 | PHYSICS |
| Chapter | KINEMATICS |
| ARIHANT PHYSICS | Level 1 |
| Medium | English |
| Academic Year | 2023-2024 |
Question 1
A particle is travelling on a curved path. In an interval Δt its speed changed from v to 2v. However, the change in magnitude of its velocity was found to be ∣∣∣−−→ΔV∣∣∣=√5v. What can you say about the direction of velocity at the beginning and at the end of the interval (Δt)?View SolutionQuestion 2
Two tourist A and B who are at a distance of 40 km from their camp must reach it together in the shortest possible time. They have one bicycle and they decide to use it in turn. ‘A’ started walking at a speed of 5kmhr1 and B moved on the bicycle at a speed of 15kmhr1. After moving certain distance B left the bicycle and walked the remaining distance. A, on reaching near the bicycle, picks it up and covers the remaining distance riding it. Both reached the camp together. (a) Find the average speed of each tourist. (b) How long was the bicycle left unused?View SolutionQuestion 3
The position time graph for a particle travelling along x axis has been shown in the figure. State whether following statements are true of false.
(a) Particle starts from rest at t=0.
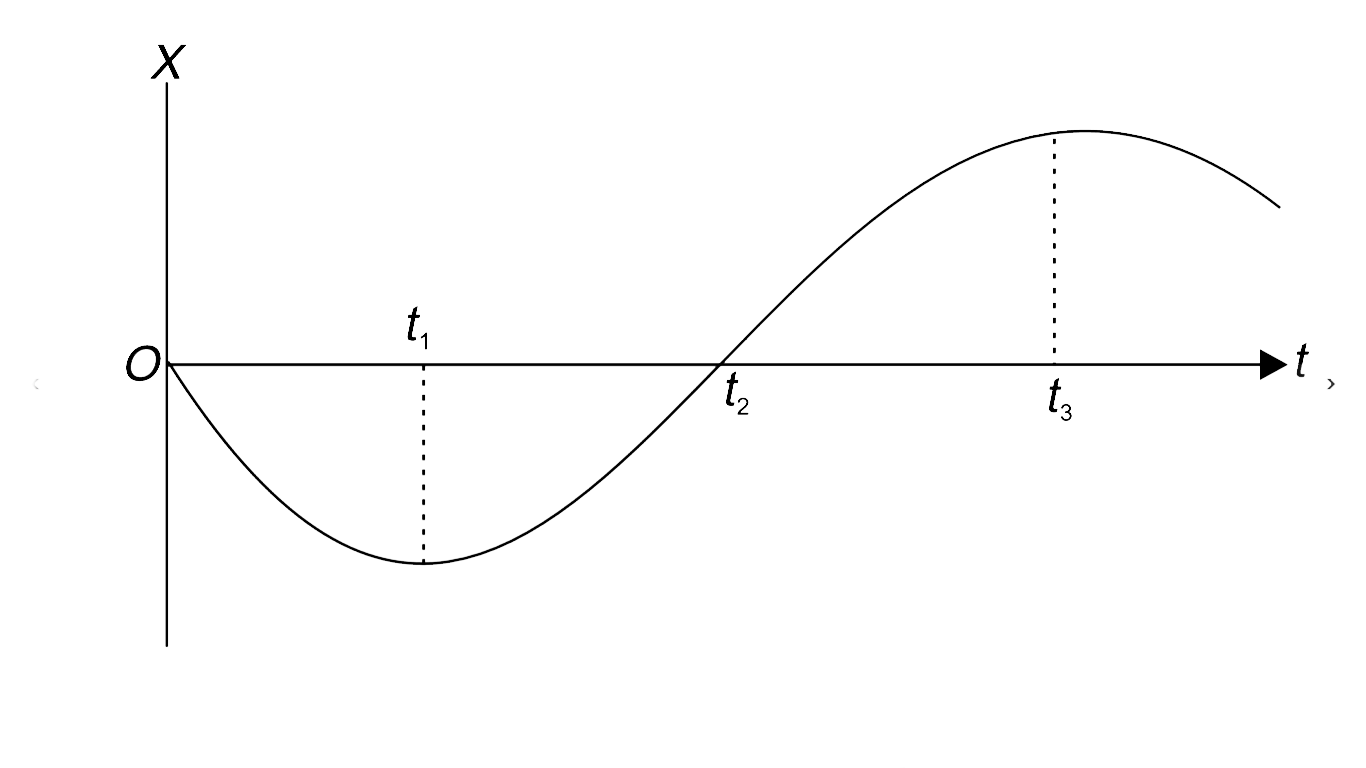
(b) Particle is retarding in the interval 0 to t1 and accelerating in the interval t1 to t2.
(c) The direction of acceleration has changed once during the interval 0 to t3View SolutionQuestion 4
The position time graph for a particle moving along X axis has been shown in the fig. At which of the indicated points the particle has
(i) negative velocity but acceleration in positive X direction.
(ii) positive velocity but acceleration in negative X direction.
(iii) received a sharp blow (a large force for negligible interval of time)?
 View Solution
View SolutionQuestion 5
A particle is moving along positive X direction and is retarding uniformly. The particle crosses the origin at time t=0 and crosses the point x=4.0m at t=2s.
(a) Find the maximum speed that the particle can possess at x=0.
(b) Find the maximum value of retardation that the particle can have.View SolutionQuestion 6
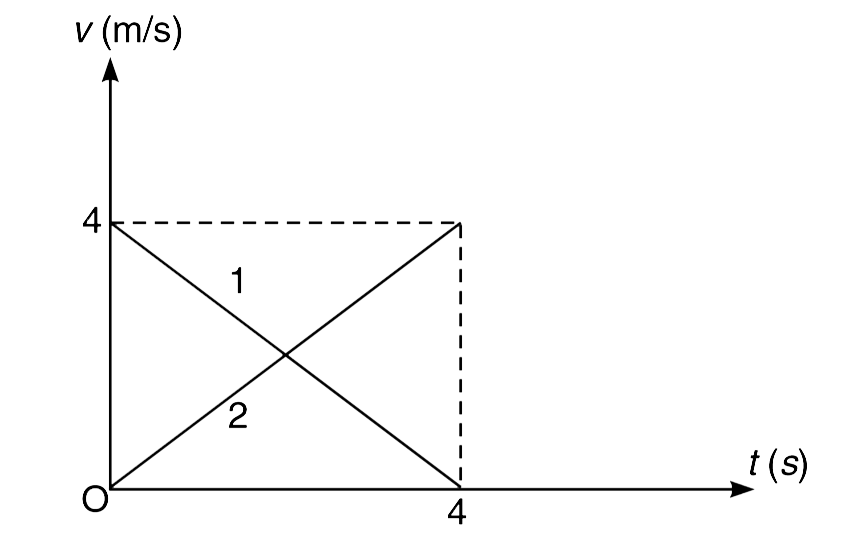
The velocity time graph for two particles (1 and 2) moving along X axis is shown in fig. At time t=0, both were at origin.
(a) During first 4 second of motion what is maximum separation between the particles? At what time the separation is maximum?
(b) Draw position (x) vs time (t) graph for the particles for the given interval.
 View Solution
View SolutionQuestion 7
A ball travelling in positive X direction with speed V0 hits a wall perpendicularly and rebounds with speed V0. During the short interaction time (Δt) the force applied by the wall on the ball varies as shown in figure.
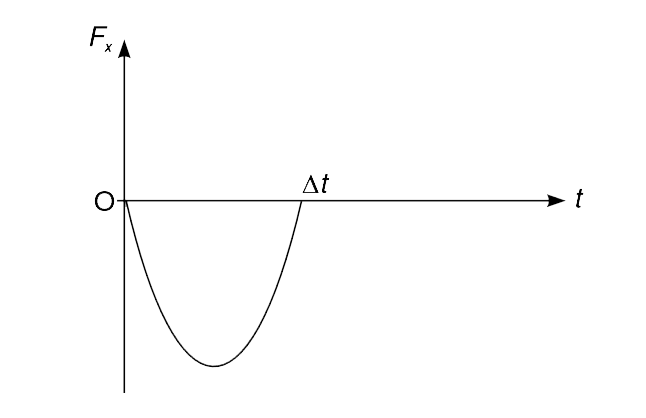
Draw the velocity-time graph for the ball during the interval 0 to ΔtView SolutionQuestion 8
For a particle moving along a straight line consider following graphs A, B, C and D. Here x, v and t are position, velocity and time respectively.
(i) In which of the graphs the magnitude of acceleration is decreasing with time?
(ii) In which of the graphs the magnitude of acceleration is increasing with time?
(iii) If the body is definitely going away from the starting point with time, which of the given graphs represent this condition.View SolutionQuestion 12
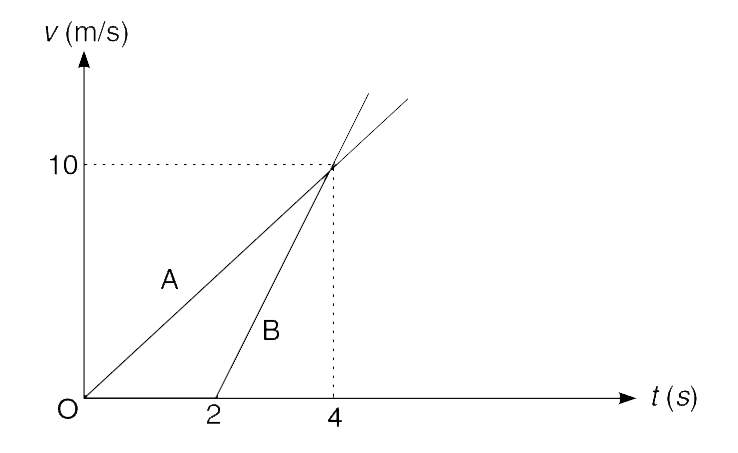
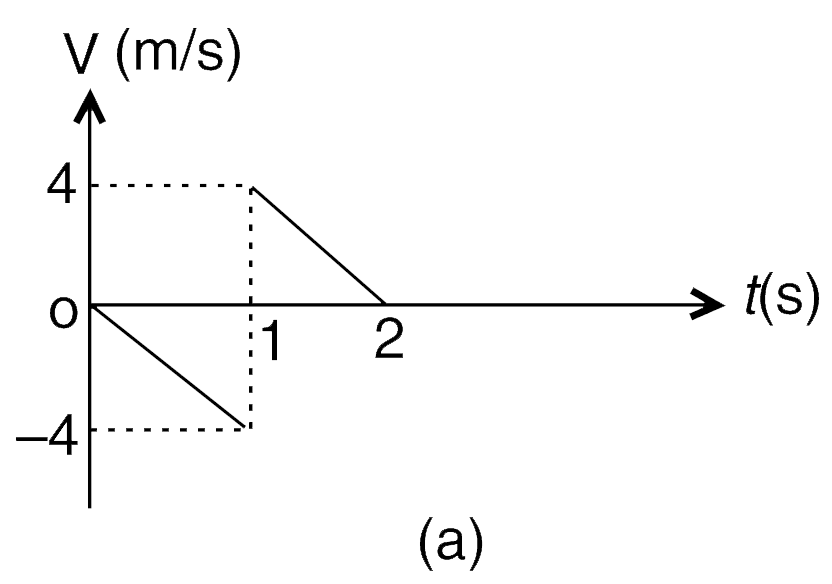
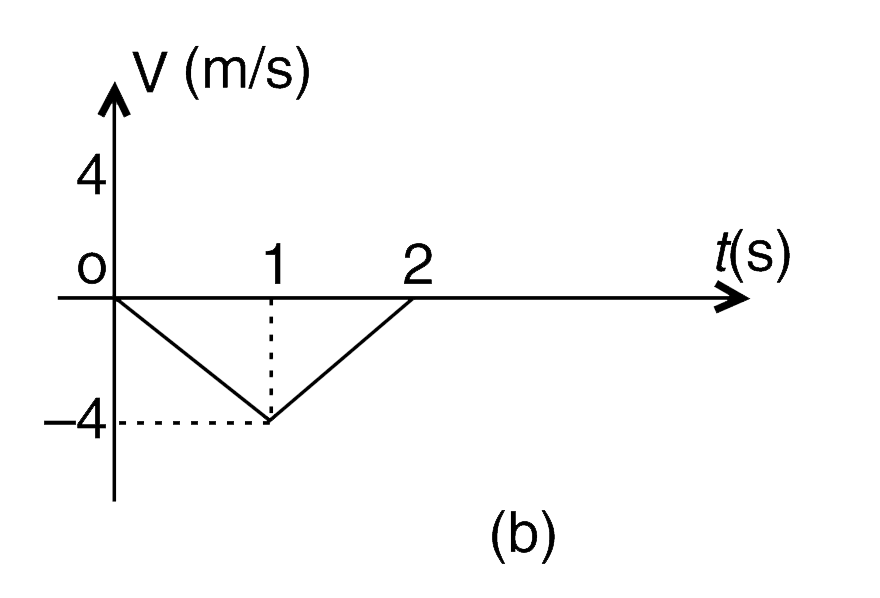
The velocity (V) – time (t) graphs for two particles A and B moving rectilinearly have been shown in the figure for an interval of 2 second.
(a) At t=1s, which of the two particles (A or B) has received a severe blow?
(b) Draw displacement (X) – time (t) graph for both of them.
 View Solution
View SolutionQuestion 13
A particle starts moving rectilinearly at time t=0 such that its velocity(v) changes with time (t) as per equation –
v=(t2–2t)m/s for 0<t<2s
=(–t2+6t–8)m/s for 2≤te4s
(a) Find the interval of time between t=0 and t=4s when particle is retarding.
(b) Find the maximum speed of the particle in the interval 0≤t≤4s. View SolutionQuestion 14
Our universe is always expanding. The rate at which galaxies are receding from each other is given by Hubble’s law (discovered in 1929 by E. Hubble). The law states that the rate of separation of two galaxies is directly proportional to their separation. It means relative speed of separation of two galaxies, presently at separation r is given by v = Hr
H is a constant known as Hubble’s parameter. Currently accepted value of H is 2.32×x10–18s–1
(a) Express the value of H in unit of
Km.s−1Mega light year
(b) Find time required for separation between two galaxies to change from r to 2r. View SolutionQuestion 16
A ball is dropped from a height H above the ground. It hits the ground and bounces up vertically to a height H2 where it is caught. Taking origin at the point from where the ball was dropped, plot the variation of its displacement vs velocity. Take vertically downward direction as positive.View SolutionQuestion 19
Two nearly identical balls are released simultaneously from the top of a tower. One of the balls fall with a constant acceleration of g1=9.80ms–2 while the other falls with a constant acceleration that is 0.1% greater than g1. [This difference may be attributed to variety of reasons. You may point out few of them]. What is the displacement of the first ball by the time the second one has fallen 1.0 mm farther than the first ball? View SolutionQuestion 21
(a) A particle starts moving at t=0 in x−y plane such that its coordinates (in cm) with time (in sec) change as x=3t and y=4sin(3t). Draw the path of the particle.
(b) If position vector of a particle is given by →r=(4t2−16t)ˆi+(3t2−12t)ˆj, then find distance travelled in first 4 sec. View SolutionQuestion 23
A ball is projected from the floor of a long hall having a roof height of H=10m. The ball is projected with a velocity of u=25ms–1 making an angle of θ=37∘ to the horizontal. On hitting the roof the ball loses its entire vertical component of velocity but there is no change in the horizontal component of its velocity. The ball was projected from point A and its hits the floor at B. Find distance AB.
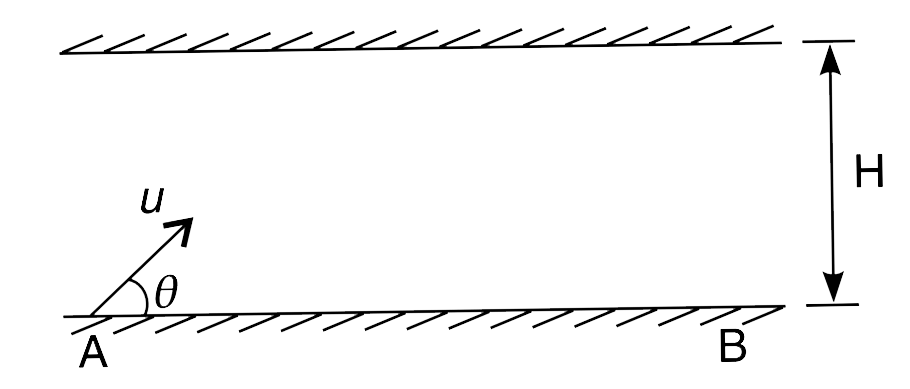 View Solution
View SolutionQuestion 24
In a tennis match Maria Sharapova returns an incoming ball at an angle that is 4° below the horizontal at a speed of 15m/s. The ball was hit at a height of 1.6 m above the ground. The opponent, Sania Mirza, reacts 0.2 s after the ball is hit and runs to the ball and manages to return it just before it hits the ground. Sania runs at a speed of 7.5m/s and she had to reach 0.8 m forward, from where she stands, to hit the ball.
(a) At what distance Sania was standing from Maria at the time the ball was returned by Maria? Assume that Maria returned the ball directly towards Sania.
(b) With what speed did the ball hit the racket of Sania?
[g=9.8m/s2]View SolutionQuestion 25
A player initially at rest throws a ball with an initial speed u=19.5m/s at an angle θ=sin−1(1213) to the horizontal. Immediately after throwing the ball he starts running to catch it. He runs with constant acceleration (a) for first 2 s and thereafter runs with constant velocity. He just manages to catch the ball at exactly the same height at which he threw the ball. Find ‘a’. Take g=10m/s2. Do you think anybody can run at a speed at which the player ran? View SolutionQuestion 26
In a cricket match, a batsman hits the ball in air. A fielder, originally standing at a distance of 12 m due east of the batsman, starts running 0.6 s after the ball is hits. He runs towards north at a constant speed of 5m/s and just manages to catch the ball 2.4 s after he starts running. Assume that the ball was hit and caught at the same height and take g=10m/s2g=10m/s2 Find the speed at which the ball left the bat and the angle that its velocity made with the vertical.View SolutionQuestion 28
A boy ‘A’ is running on a circular track of radius R. His friend, standing at a point O on the circumference of the track is throwing balls at speed u=√gR. Balls are being thrown randomly in all possible directions. Find the length of the circumference of the circle on which the boy is completely safe from being hit by a ball.
 View Solution
View SolutionQuestion 29
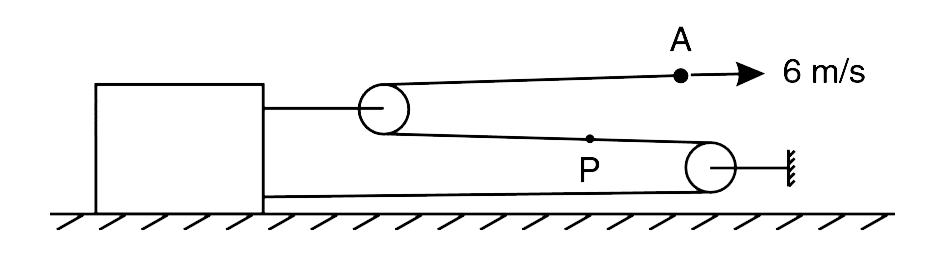
A rectangular cardboard ABCD has dimensions of 40cm×x30cm. It is moving in a direction perpendicular to its shorter side at a constant speed of 2cm/s. A small insect starts at corner A and moves to diagonally opposite corner C. On reaching C it immediately turns back and moves to A. Throughout the motion the insect maintains a constant speed relative to the board. It takes 10 s for the insect to reach C starting from A. Find displacement and distance travelled by the insect in reference frame attached to the ground in the interval the insect starts from A and comes back to A.
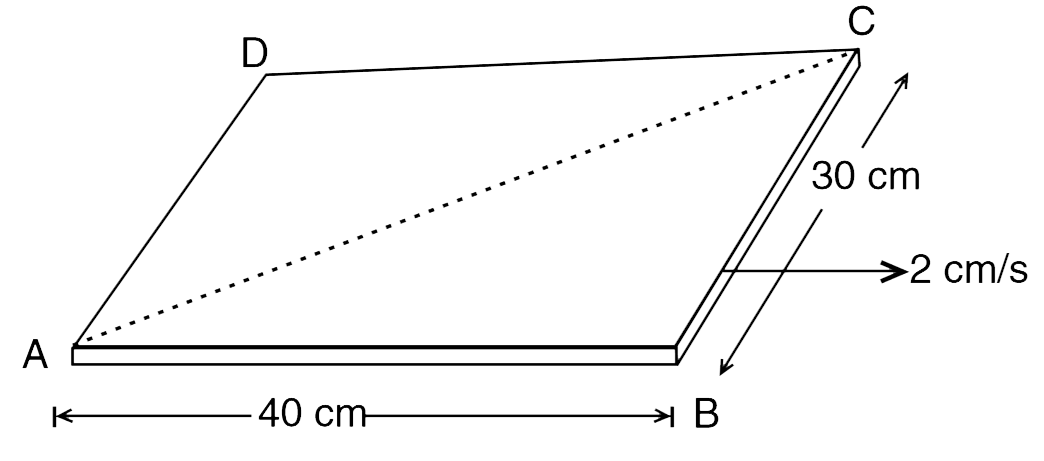 View Solution
View SolutionQuestion 30
Two particles A and B separated by 10 m at time t=0 are moving uniformly. A is moving along line AB at a constant velocity of 4m/s and B is moving perpendicular to the velocity of A at a constant velocity of 5m/s. After what time the two particles will be nearest to each other?
 View Solution
View SolutionQuestion 31
Four cars are moving along a straight road in the same direction. Velocity of car 1 is 10m/s. It was found that distance between car 1 and 2 is decreasing at a rate of 2m/s, whereas driver in car 4 observed that he was nearing car 2 at a speed of 8m/s. The gap between car 2 and 3 is decreasing at a rate of 3m/s.

(a) t=0, after how much time t0 will the driver of car 2 see for the first time, that another car overtakes him?
(b) Which car will be first to overtake car 1? View SolutionQuestion 33
A physics professor was driving a Maruti car which has its rear wind screen inclined at θ=37∘ to the horizontal. Suddenly it started raining with rain drops falling vertically. After some time the rain stopped and the professor found that the rear wind shield was absolutely dry. He knew that, during the period it was raining, his car was moving at a constant speed of Vc=20km/hr.[tan37∘=0.75]
(a) The professor calculated the maximum speed of vertically falling raindrops as Vmax. What is value of Vmax that he obtained.
(b) Plot the minimum driving speed of the car vs. angle of rear wind screen with horizontal (θ) so as to keep rain off the rear glass. Assume that rain drops fall at constant speed VrView SolutionQuestion 34
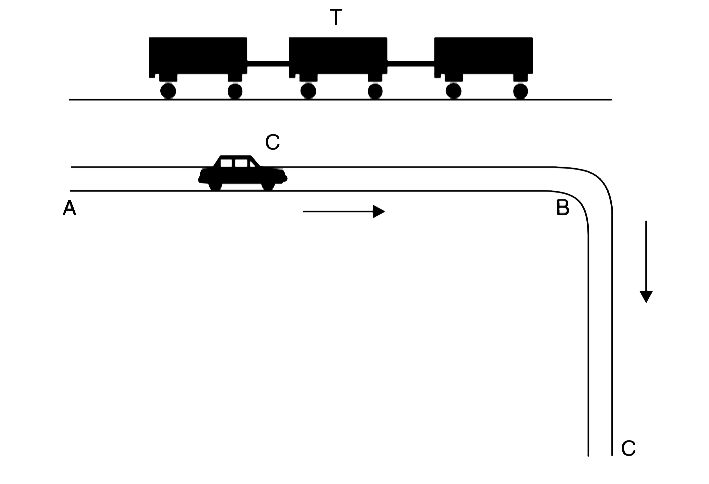 A train(T) is running uniformly on a straight track. A car is travelling with constant speed along section AB of the road which is parallel to the rails. The driver of the car notices that the train is having a speed of 7m/s with respect to him. The car maintains the speed but takes a right turn at B and travels along BC. Now the driver of the car finds that the speed of train relative of him is 13m/s. Find the possible speeds of the car.View Solution
A train(T) is running uniformly on a straight track. A car is travelling with constant speed along section AB of the road which is parallel to the rails. The driver of the car notices that the train is having a speed of 7m/s with respect to him. The car maintains the speed but takes a right turn at B and travels along BC. Now the driver of the car finds that the speed of train relative of him is 13m/s. Find the possible speeds of the car.View SolutionQuestion 35
 A police car B is chasing a culprit’s car A. Car A and B are moving at constant speed V1=108km/hr and V2=90km/hr respectively along a straight line. The police decides to open fire and a policeman starts firing with his machine gun directly aiming at car A. The bullets have a velocity u=305m/s relative to the gun. The policeman keeps firing for an interval of T0=20s. The Culprit experiences that the time gap between the first and the last bullet hitting his car is Δt. Find Δt. View Solution
A police car B is chasing a culprit’s car A. Car A and B are moving at constant speed V1=108km/hr and V2=90km/hr respectively along a straight line. The police decides to open fire and a policeman starts firing with his machine gun directly aiming at car A. The bullets have a velocity u=305m/s relative to the gun. The policeman keeps firing for an interval of T0=20s. The Culprit experiences that the time gap between the first and the last bullet hitting his car is Δt. Find Δt. View SolutionQuestion 36
A chain of length L is supported at one end and is hanging vertically when it is released. All of the chain falls freely with acceleration g. The moment, the chain is released a ball is projected up with speed u from a point 2 L below the point of support. Find the interval of time in which the ball will cross through the entire chain.View SolutionQuestion 38
A small cart A starts moving on a horizontal surface, assumed to be x-y plane along a straight line parallel to x-axis (see figure) with a constant acceleration of 4m/s2. Initially it is located on the positive y-axis at a distance 9 m from origin. At the instant the cart starts moving, a ball is rolled along the surface from the origin in a direction making an angle 45° with the x-axis. The ball moves without friction at a constant velocity and hits the cart.
(a) Describe the path of the ball in a reference frame attached to the cart.
(b) Find the speed of the ball.
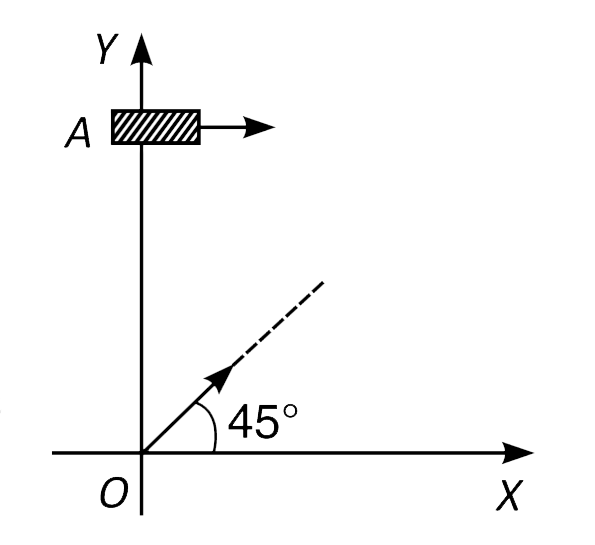 View Solution
View SolutionQuestion 39
(a) A boy on a skateboard is sliding down on a smooth incline having inclination angle q. He throws a ball such that he catches it back after time T. With what velocity was the ball thrown by the boy relative to himself ?

(b) Barrel of an anti aircraft gun is rotating in vertical plane (it is rotating up from the horizontal position towards vertical orientation in the plane of the fig). The length of the barrel is L=√2m and barrel is rotating with angular velocity ω=2rad/s. At the instant angle θ is 45° a shell is fired with a velocity 2√2m/s with respect to the exit point of the barrel. The tank recoils with speed 4m/s. What is the launch speed of the shell as seen from the ground?
 View Solution
View SolutionQuestion 40
long piece of paper is10 cm wide and is moving uniformly along its length with a velocity of 2cm/s. An ant starts moving on the paper from point A and moves uniformly with respect to the paper. A spider was located exactly opposite to the ant just outside the paper at point B at the instant the ant started to move on the paper. The spider, without moving itself, was able to grab the ant 5 second after it (the ant) started to move. Find the speed of ant relative to the paper.
 View Solution
View SolutionQuestion 41
Two particles A and B are moving uniformly in a plane in two concentric circles. The time period of rotation is TA=8 minute and TB=11 minute respectively for the two particles. At timet=0, the two particles are on a straight line passing through the centre of the circles. The particles are rotating in same sense. Find the minimum time when the two particles will again fall on a straight line passing through the centre. View SolutionQuestion 43
Two paper discs are mounted on a rotating vertical shaft. The shaft rotates with a constant angular speed ω and the separation between the discs is H. A bullet is fired vertically up so that it pierces through the two discs. It creates holes H1 and H2 in the lower and the upper discs. The angular separation between the two holes (measured with respect to the shaft axis) is θ. Find the speed (v) of the bullet. Assume that the speed of the bullet does not change while travelling through distance H and that the discs do not complete even one revolution in the interval the bullet pierces through them.
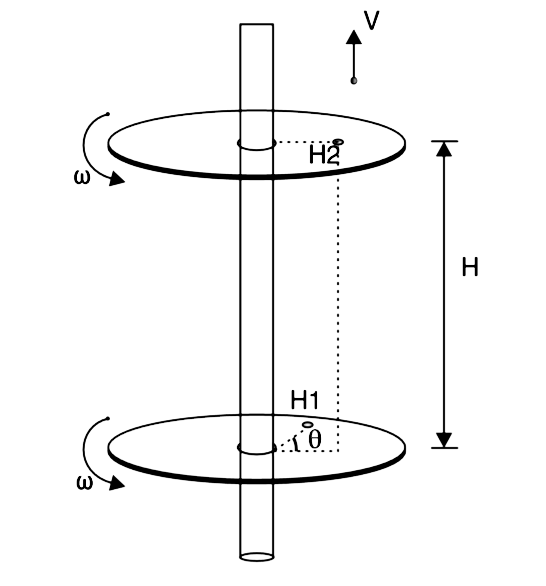 View Solution
View SolutionQuestion 44
(a) A car moves around a circular arc subtending an angle of 60° at the centre. The car moves at a constant speed u0 and magnitude of its instantaneous acceleration is a0. Find the average acceleration of the car over the 60° arc.
(b) The speed of an object undergoing uniform circular motion is 4m/s. The magnitude of the change in the velocity during 0.5 sec is also 4m/s. Find the minimum possible centripetal acceleration (in m/s2) of the object.View SolutionQuestion 45
A particle is fixed to the edge of a disk that is rotating uniformly in anticlockwise direction about its central axis. At time t=0 the particle is on the X axis at the position shown in figure and it has velocity v
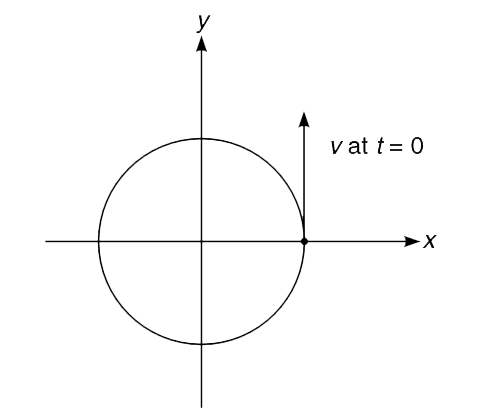
(a) Draw a graph representing the variation of the x component of the velocity of the particle as a function of time.
(b) Draw the y-component of the acceleration of the particle as a function of time. View SolutionQuestion 46
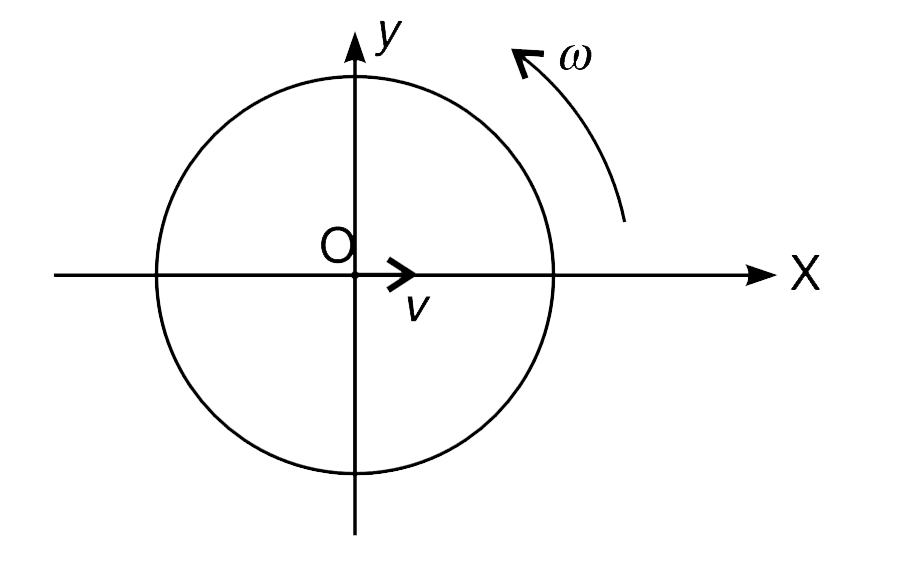
A disc is rotating with constant angular velocity ω in anticlockwise direction. An insect sitting at the centre (which is origin of our co-ordinate system) begins to crawl along a radius at time t=0 with a constant speed V relative to the disc. At time t=0 the velocity of the insect is along the X direction.
(a) Write the position vector (→r) of the insect at time ‘t’.
(b) Write the velocity vector (→v) of the insect at time ‘t’.
(c) Show that the X component of the velocity of the insect become zero when the disc has rotated through an angle θ given by tanθ=1θ.
 View Solution
View SolutionQuestion 47
(a) A point moving in a circle of radius R has a tangential component of acceleration that is always n times the normal component of acceleration (radial acceleration). At a certain instant speed of particle is v0. What is its speed after completing one revolution?
(b) The tangential acceleration of a particle moving in xy plane is given by at=a0cosθ. Where a0 is a positive constant and q is the angle that the velocity vector makes with the positive direction of X axis. Assuming the speed of the particle to be zero at x=0, find the dependence of its speed on its x co-ordinate. View SolutionQuestion 48
A particle is rotating in a circle. When it is at point A its speed is V. The speed increases to 2 V by the time the particle moves to B. Find the magnitude of change in velocity of the particle as it travels from A to B. Also, find −→VA−−→ΔV, where −→VA is its velocity at point A and −−→ΔV is change in velocity as it moves from A to B. View Solution