Eexercies from BHARATI BHAWAN PHYSICS Chapter 24 SIMPLE HARMONIC MOTION for Class 11

Question 1

Question 2

Question 3

Question 4

Question 5

Question 6

Find the phase difference between two particles executing simple harmonic motion with the same frequency if they are found inn the states shown in the figures at four different points of time.

Question 7

Question 8

Question 9

Question 10

Question 11

Question 12

Question 13

Question 14

Question 15

Question 16

Question 17

Question 18

Question 19

Question 20

Question 21

A solid cylinder of mass $m$ is attached to a horizontal spring with force constant $k$. The cylinder can roll without slipping along the horizontal plane. (See the accompanying figure.) Show that the center of mass of the cylinder executes simple harmonic motion with a period $T=2\pi \sqrt{\frac{3m}{2k}}$, if displaced from mean position.

Question 22

Question 23

Question 24

Question 25

A body of mass m falls from a height h on to the pan of a spring balance, figure, The masses of the pan and spring are negligible. The spring constant of the spring is k. The body gets attached to the pan and starts executing S.H.M. in the vertical direction. Find the amplitude and energy of oscillation.

Question 26

Question 27

Question 28

Question 29

Question 30

Question 31

Question 32

Question 33

A small sleeve of mass $m=1/10kg$ can move along the diameter of a horizontal disc, which slides without friction along a guide rode. The sleeve is tied to the end of the rod with the aid of a massless spring whose force constant $k=10N/m$. When the spring is not under tension, the sleeve is at the oscillations of the sleeve when the disc rotates about its axis at the angular speed $\omega$ equal to a) 6 rad/s, b) 15 rad/s.

Question 34

Question 35

A block of mass $m_1=1kg$ is attached to a spring of force constant $k=24N/cm$ at one end and attached to a string tensioned by mass $m_2=5kg$ . Dedcue the frequency of oscillaitons of the system. If $m_2$ is initially supported in hand and then suddenly released, find

$\left(a\right)$ instantaneous tension just after $m_2$ is released . ltbr> $\left(b\right)$ the maximum displacement of $m_1$.
$\left(c\right)$ the maximum and minimum tensions in the string during oscillations.

Question 36

Question 37

Find the frequency of oscillations of the system in the figure. The bar is rigid and light.
[Hint: A spring of force constant $k_1$ at a distance a is equivalent to a spring of force constant $k_1\left(\frac{a}{b}\right)o^2$ at a distance b)

Question 38

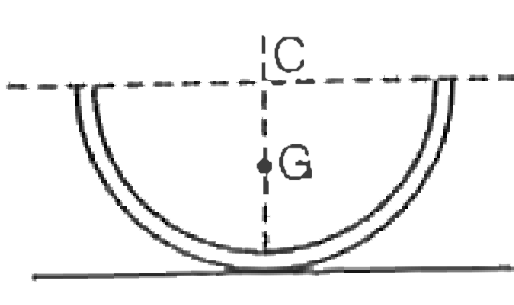
A pipe in the form of a half ring is placed on a horizontal surface. If it is rotated through a small angle, and then released, assuming that it rolls without sliding determine the period of oscillations. The center of gravity of such a body is at distance $\frac{2r}{\pi })$ from the center where r is the radius of the ring.
Hint: $(\overrightarrow{–}\left(c\right)=\alpha r\hat{i}$ and
$\overrightarrow{a_c}=\overrightarrow{a_c}+{\left({\overrightarrow{a}}_{G/c}\right)}_{\text{tangent}}+{\left({\overrightarrow{a}}_{G/c}\right)}_{\text{normal}}$

Question 39

An endless cord consists of lengths 2l and $2l^{\prime }$ and their masses per unit length are m and $m^{\prime }$. It is placed in stable equilibrium over a smooth peg as shown in the figure. It is slightly displaced and left to itself. Show that motion is simple harmonic. Find the period of oscilattions.