Solved Example from CENGAGE PHYSICS (ENGLISH) CALORIMETRY for Class 11
| Class 11 | PHYSICS |
| Chapter | CALORIMETRY |
| CENGAGE PHYSICS (ENGLISH) | Solved Example |
| Medium | English |
| Academic Year | 2023-2024 |
Question 6
A 60 kg boy running at 5.0m/s while playing basketball falls down on the floor and skids along on his leg until he stopes. How many calories of heat are generated between his leg and the floor?
Assume that all this heat energy is confined to a volume of 2.0cm3 of his flesh. What will be temperature change of the flesh? Assume c=1.0calg∘C and ρ=950kgm3 for flesh. View SolutionQuestion 10
The air temperature above coastal areas is profoundly influenced by the large specific heat of water. One reason is that the energy released when 1m3 of water cools by 1∘C will raise the temperature of a much larger volume of air by 1∘C. Find this volume of air. The specific heat of air is approximately 1kJ/kg∘C. Take the density of air to be 1.3kg/m3.View SolutionQuestion 12
Calculate the heat of fusion of ice from the following data of ice at 0∘C added to water. Mass of calorimeter=60g, mass of calorimeter+ water =460g,
mass of calorimeter+water+ice=618g, initial temperature of water =38∘C, final temperature of the mixture=5∘C. The specific heat of calorimeter =0.10cal/g/∘C. Assume that the calorimeter was also at 0∘C initiallyView SolutionQuestion 15
When a block of metal of specific heat 0.1cal/g/∘C and weighing 110 g is heated to 100∘C and then quickly transferred to a calorimeter containing 200g of a liquid at 10∘C, the resulting temperature is 18∘C. On repeating the experiment with 400 g of same liquid in the same calorimeter at same initial temperature, the resulting temperature is 14.5∘C. find
a. Specific heat of the liquid.
b. The water equivalent of calorimeter.View SolutionQuestion 17
A tube leads from a flask in which water is boiling under atmospheric pressure to a calorimeter. The mass of the calorimeter is 150 g, its specific heat capacity is 0.1cal/g/∘C, and it contains originally 340g of water at 15∘C. Steam is allowed to condense in the colorimeter until its temperature increases to 71∘C, after which total mass of calorimeter and contents are found to be 525g. Compute the heat of condensation of steam.View SolutionQuestion 22

A substance is in the solid form at 0∘C. The amount of heat added to this substance and its temperature are plotted in the following graph. If the relative specific heat capacity of the solid substance is 0.5, find from the graph (i) the mass of the substance, (ii) the specific latent heat of the melting process and (ii) the specific heat of the substance in the liquid state.
Specific heat capacity of water =1000cal/kg/KView SolutionQuestion 23
Two bodies of equal mass m are heated at a uniform rate under identical conditions . Their change in temperature are shown graphically in figure .
(i) what are their melting points ?
(ii) what is the ratio of their latent heats?
(iii) what is the ratio of their specific heats?
 View Solution
View SolutionQuestion 24

The rectangular plate shown if Fig. 1.7 has an area Ai. If the temperature increases by ΔT, each dimension increases according to ΔL=αLΔT, where α is the average coefficient of linear expansion. Show that the increase in area is ΔA=2αAiΔT. What approzimation does this expansion assume?View SolutionQuestion 26
A metal rod (A) of 25cm length expands by 0.050cm when its temperature is raised from 0∘C to 100∘C. Another rod (B) of a different metal of length 40cm expands by 0.040cm for the same rise in temperature. A third rod ( C) of 50cm length is made up of pieces of rods (A) and (B) placed end to end expands by 0.03cm on heating from 0∘C to 50∘C. Find the lengths of each portion of the composite rod.View SolutionQuestion 29
A steel rail 30 m long is firmly attached to the roadbed only at its ends. The sun raises the temperature of the rail by 5∘C, causing the rail to buckle. Assuming that the buckled rail consists of two straight parts meeting in the centre, calculate how much the centre of the rail rises. coefficient of linear expansion of steel is 12×10−6/K.View SolutionQuestion 30
A small quantity of a liquid which dows not mix with water sinks to the bottom at 20∘C, the densities of the liquid and water being 1021 and 990kg/m3, respectively. To what teperature must the mixture be uniformly heated in order that the liquid forms globules which just float on water ? the cubical expansion of the liquid and water over the temperature ranges is 85×10−5/K and 45×10−5/K respectively. View SolutionQuestion 31
A one litre flask contains some mercury. It is found that at different temperatures the volume of air inside the flask remains tha same. What is the volume of mercury in the flask? Given the cofficients of linear expansion of glass is 9×10−6/∘C and the coefficient of volume expansion of mercury is 1.8×10−4/∘CView SolutionQuestion 32
A hollow aluminium cylinder 20.0 cm deep has an internal capacity of 2.000 L at 20.0∘ C. It is completely filled with tupentine and then slowly warmed to 80.0∘C a. How much turpentine overflows? B. If the cylindre is then cooled back to 20.0∘C, how far below the cylinder's rim dows the tupentine's surface recede?View SolutionQuestion 33
A glass flask whose volume is exactly 1000cm3 at 0∘C is filled level full of mercury at this temperature. When the flask and mercury are heated to 100∘C, 15.2cm3 of mercury overflows. The coefficient of cubical expansion of Hg is 1.82×10−4/∘C. Compute the coefficient of linear expansion of glass.View SolutionQuestion 34
A 250cm3 glass bottle is completely filled with water at 50∘C. The bottle and water are heated to 60∘C. How much water runs over if:
a. the expansion of the bottle is neglected:
b. the expansion of the bottle is included? Given the coefficient of areal expansion of glass β=1.2×10−5/K and γwater=60×10−5/∘C.View SolutionQuestion 37
A copper and a tungsten plate having a thickness σ=2mm eacha re riveted together so that at 0∘C They form a flat bimetallic plate. Find the average radius of cuvature of this plate at t=200∘C. The coefficients of linear expansion for copper and tungsten are
αcu=1.7×10−5/K and αW=0.4×10−5/K, respectively.View SolutionQuestion 38
A clock with a brass pendulum shaft keeps correct time at a certain temperature.
a. How closely must the temperature be controlled if the clock is not to gain or lose more that 1 s a day? Does the answer depend on the period of the pendulum?
b. Will an increase of temperature cause the clock to gain or lose? (αbrass=2×10−5/∘C)View SolutionQuestion 41
Two rods of different metals having the same area of cross section A are placed between the two massive walls as shown is Fig. The first rod has a length l1, coefficient of linear expansion α1 and Young's modulus Y1. The correcsponding quantities for second rod are l2,α2 and Y2. The temperature of both the rods is now raised by t∘C.
i. Find the force with which the rods act on each other (at higher temperature) in terms of given quantities.
ii. Also find the length of the rods at higher temperature.
 View Solution
View SolutionQuestion 42
Two rods of equal cross sections, one of copper and the other of steel, are joined to form a composite rod of length 2.0 m at 20∘C, the length of the copper rod is 0.5 m. When the temperature is raised to 120∘C, the length of composite rod increases to 2.002m. If the composite rod is fixed between two rigid walls and thus not allowed to expand, it is found that the lengths of the component rods also do not change with increase in temperature. Calculate Young's moulus of steel. (The coefficient of linear expansion of copper, αc=1.6×10−5∘C and Young's modulus of copper is 1.3×1013N/m2).View SolutionQuestion 44
A barometer with a brass scale reads 755 mm on a day when the temperatures is 25∘C. If the scale is correctly graduated at 0∘C, find the true pressure at 0∘C (interms of height of Hg) given that the coefficient of linear expansion of brass is 18×10−6/K. Coefficient of cubical expansion of mercury=182×10−6/K.View SolutionQuestion 47
A refrigerator is thermally equivalent to a box of cork board 90 mm thick and 6m2 in iner surface area, the thermal conductivity of cork being 0.05W/mK. The motor of the refrigerator runs 15% of the time while the door is closed. The inside wall of the door, when it is closed is kept, on an average, 22∘C below the temperature of the outside wall. The rate at which heat is taken from the interior wall while the motor is running is View SolutionQuestion 48
Water is being boiled in a flat bottomed kettle placed on a stove . The area of the bottom is 300cm2 and the thickness is 2 mm. If the amount of steam produced is 1 g −1min, then the difference of the temperature between the inner and outer surfaces of the bottom is (thermal conductivity of the material of the lettle =0.5calcm−1^(∘)Cs−1 and latent heat of the steam is equal to to 540calg−1) View SolutionQuestion 49
A closed cubical box is made of perfectly insulating material and the only way for heat to enter or leave the box is through two solid cylindrical metal plugs, each of cross sectional area 12cm2 and length 8cm fixed in the opposite walls of the box. The outer surface of one plug is kept at a temperature of 100∘C . while the outer surface of the plug is maintained at a temperature of 4∘C . The thermal conductivity of the material of the plug is 2.0Wm−1C−1 . A source of energy generating 13W is enclosed inside the box. Find the equilibrium temperature of the inner surface of the box assuming that it is the same at all points on the inner surface.View SolutionQuestion 50
Two metal cubes A and B of same size are arranged as shown in figure. The extreme ends of the combination are maintained at the indicated temperature. The arrangement is thermally insulated. The coefficients of thermal conductivity of A and B are 300W/m∘C and 200W/m∘C, respectively. After steady state is reached, the temperature t of the interface will be________.
 View Solution
View SolutionQuestion 51
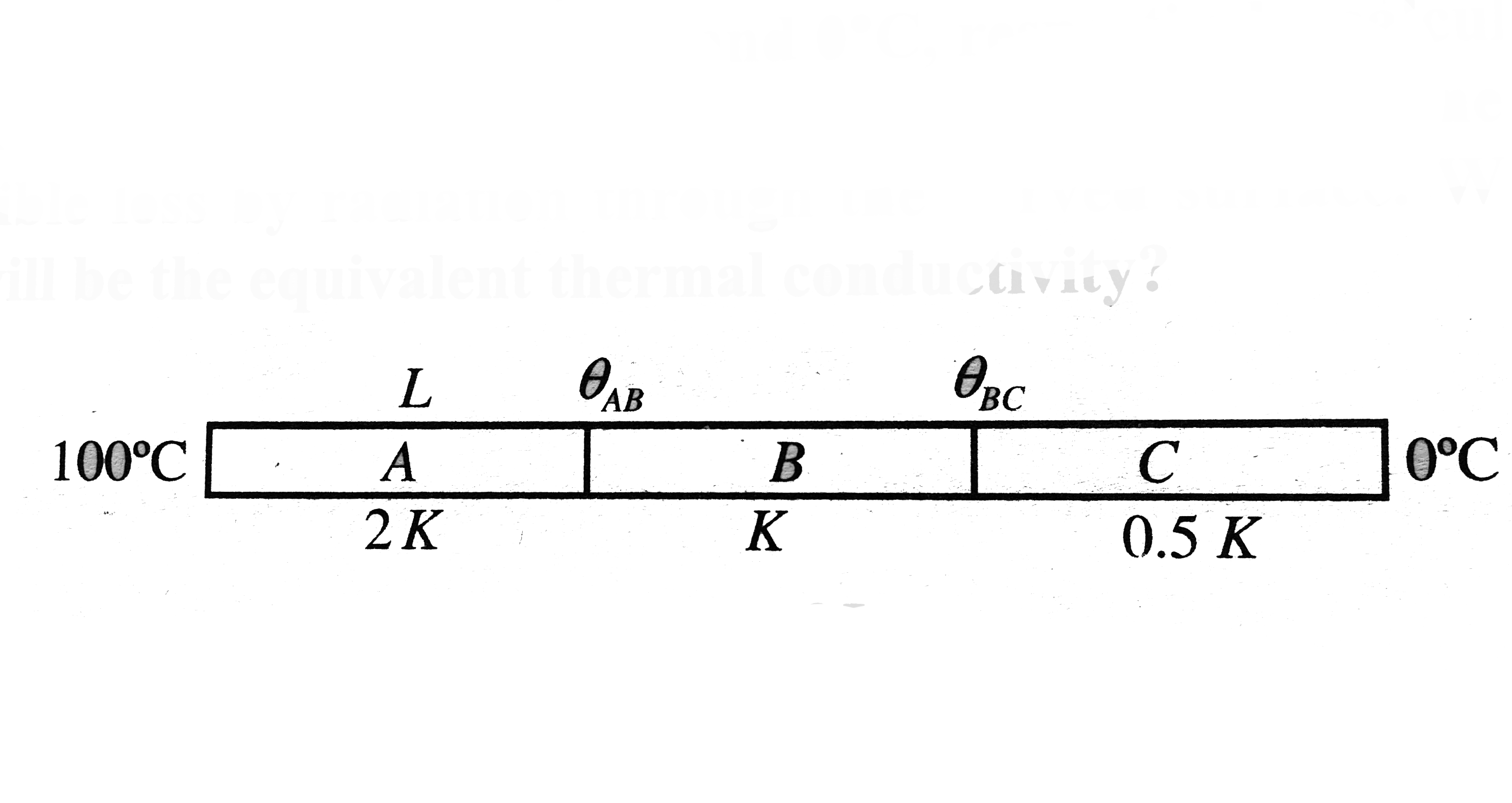
Three cylindrical rods A, B and C of equal lengths and equal diameters are joined in series as shown if Fig. Their thermal conductivities are 2K, K and 0.5K, respectively. In steady state, if the free ends of rods A and C are at 100∘C and 0∘C, respectively, calculate the temperature at the two junction points. Assume negligible loss by radiaiotn through the curved surface. What will be the equivalent thermal conductivity?View SolutionQuestion 53
One end of a uniform brass rod 20 cm long and 10cm2 cross-sectional area is kept at 100∘C. The other end is in perfect thermal contact with another rod of identical cross-section and length 10 cm. The free end of this rod is kept in melting ice and when the steady state has been reached, it is found that 360 g of ice melts per hour. Calculate the thermal conductivity of the rod, given that the thermal conductivity of brass is 0.25cal/scm∘CandL=80cal/g.View SolutionQuestion 54
An electric heater is used in a room of total wall area 137m2 to maintain a temperature of 20∘C inside it, when the outside temperature is −10∘C .The walls have three different layers of materials. The innermost layer is of wood of thickness 2.5cm, the middle layer is of cement of thickness 1.0cm and the outermost layer is of brick of thickness 25.0cm. Find the power of the electric heater. Assume that there is no heat loss through the floor and the celling. The thermal conductivities of wood, cement and brick are 0.125Wm−1C−1 , 1.5Wm−1C−1 . and 1.0Wm−1C−1 respectively.
View SolutionQuestion 55
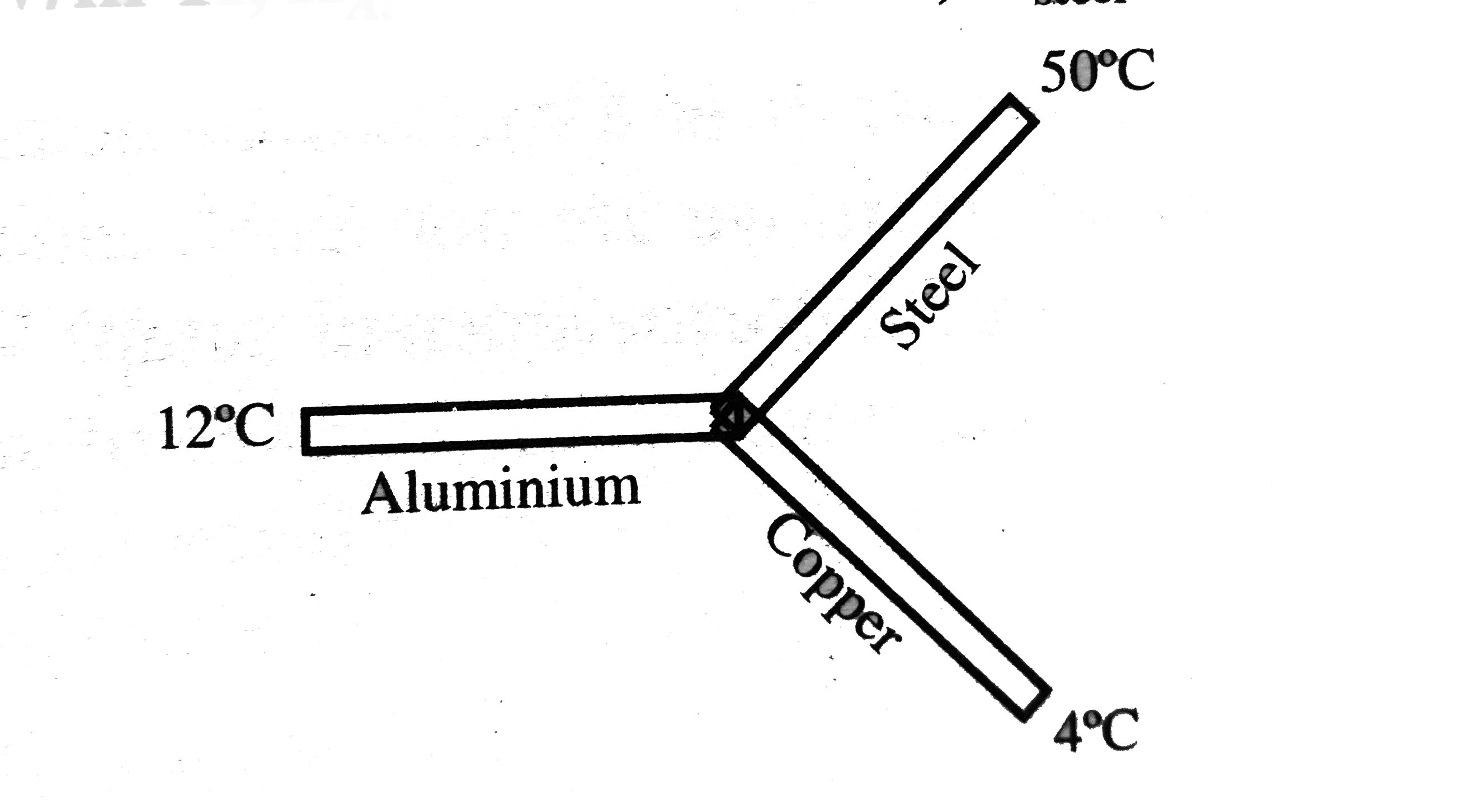
Three identical rods of length 1 m each, having cross-sectional area of 1cm2 each and made of aluminium, copper and steel, respectively, are maintained at temperatures of 12∘C,4∘C and 50∘C, respectively, at their separate ends. Find the teperature of their common junction.
[KCu=400W/m−K,KAl=200W/m−K,Ksteel=50W/m−K]View SolutionQuestion 56
An electric heater of surface area 200cm2 emits radiant energy of 60 kJ at time interval of 1 min. Determine its emissive power. If its emissivity be 0.45, what would be the radiant energy emitted by a black body in one hour, identical to the electrical heater in all respects?View SolutionQuestion 59
A copper sphere is suspended in an evacuated chamber maintained at 300 K . The sphere is maintained at a constant temperature of 500 K by heating it electrically. A total of 210 W of electric power is needed to do it. When the surface of the copper sphere is completely blackened, 700 W is needed to maintain the same temperature of the sphere. Calculate the emissivity of copper. View SolutionQuestion 60
Two bodies A and B have thermal emissivities of 0.01 and 0.81 respectively. The outer surface areas of the two bodies are same. The two bodies emit total radiant power at the same rate. The wavelength λB corresponding to maximum spectral radiancy from B is shifted from the wavelength corresponding to maximum spectral radiancy in the radiation from A by 1.0 μm. If the temperature of A is 5802 K, calculate (a) the temperature of B, (b) wavelength λB. View SolutionQuestion 61
The emissivity of tungsten is aproximately 0.35. A tungsten sphere 1 cm in radius is suspended within a large evacuated enclosure whose walls are at 300 K. What power input is required to maintain the sphere at a temperature of 3000 K if heat conduction along the support is neglected?σ=5.67×10−8 SI units.View SolutionQuestion 62
A solid copper sphere of density ρ, specific heat c and radius r is at temperature T1. It is suspended inside a chamber whose walls are at temperature 0K. What is the time required for the temperature of sphere to drop to T2? Take the emmissivity of the sphere to be equal to e.View SolutionQuestion 64
Two identical spheres A and B are suspended in an air chamber which is maintained at a temperature of 50∘C. Find the ratio of the heat lost per second from the surface of the spheres if
a. A and B are at temperatures 60∘C and 55∘C, respectively.
b. A and B are at temperatures 250∘C and 200∘C, respectively.View SolutionQuestion 73
The intensity of solar radiation just outside the earth's atmosphere is measured to be 1.4kW/m2. If the radius of the sun 7×108m, while the earth-sun distance is 150×106km, then find
i. the intensity of salr radiation at the surface of the sun.
ii. the temperature at the surface of the sun assuming it to be a black body,
iii. the most probable wavelength in solar radiation.View SolutionQuestion 75
A colorimeter contains 400g of water at a temperature of 5∘C. Then, 200g of water at a temperature of +10∘C and 400g of ice at a temperature of −60∘C are added. What is the final temperature of the contents of calorimeter?
Specific heat capacity of water −1000 cal/kg/K
Specific latent heat of fusion of ice =80×1000 cal/kg
Relative specific heat of ice =0.5View SolutionQuestion 77
A solar cooker consists of a curved reflecting surface that concentrates sunlight onto the object to Earth's surface at the location is 6W/m2. The cooker face the sun and has a face diameter of 0.600m. Assume 40.0% of the incident energy is tranferred to 0.500L of water in an open container, initially at 20.0∘C. Over what time interval does the water completely boil away? (Ignore the heat capacity of the container.)
 View Solution
View SolutionQuestion 78
An iron wire AB of length 3m at 0∘C is stretched between the oppsote walls of a brass casing at 0∘C. The diameter of the wire is 0.6mm. What extra tension will be set up in the wire when the temperature of the system is rasied to 40∘C?
Given abrass=18×10−6/k
airon=12×10−6/K
Yiron=21×1010N/m2View SolutionQuestion 79
A composite rod is made by joining a copper rod, end to end, with a second rod of different material but of the same area of cross section. At 25∘C, the composite rod is 1m long and the copper rod is 30cm long. At 125∘C the length of the composte rod increases by 1.91mm. When the composite rod is prevented from expanding by bolding it between two rigid walls, it is found that the constituent reds have remained unchanged in length in splite of rise of temperature. Find yong's modulus and the coefficient of linear expansion of the second red (Y of copper =1.3×1010N/m2 and a of copper =17×10−6/K).View SolutionQuestion 80
How should 1kg of water at 50∘C be divided in two parts such that if one part is turned into ice at 0∘C. It would release sufficient amount of heat to vapourize the other part. Given that latent heat of fusion of ice is 3.36×105J/Kg. Latent heat of vapurization of water is 22.5×105J/kg and specific heat of water is 4200J/kgK. View SolutionQuestion 81
A layer of ice of 0∘C of thickness x1 is floating on a pond. If the atmospheric temperature is −7∘C. Show that the time taken for thickness of the layer of ice to increase from x1 to x2 is given by
t=pL2kT(x22−x21)
where p is the density of ice, k its thermal conductivity and L is the latent heat of fusion of ice. View SolutionQuestion 82
A cylindrical rod of heat capacity 120J/K in a room temperature 27∘C is heated internally by heater of power 250W, The steady state temperature attained by the rod is 37∘C. Fin the following:
(a) The initial rate of increse in temperature
(b) The steady state rate of emission of radiant heat.
If the heater is switched off, find
(c) The initial rate of decrease is temperature
(d) The rate of decrease in temperature of the cylinder when its temperature falls to 31∘C and
(e) The maximum amount of heat lost by the cylinderView SolutionQuestion 83
Three rods of material X and three rods of material Y are connected as shown in the figure. All the rods are of identical length and cross-sectional area. If the end A is maintained at 60∘C and the junction E at 10∘C. Calculate the temperature of the junction B, C and D. The thermal conductivity of X is 0.92cal/sec−cm∘C and that of Y is 0.46cal/sec−cm−∘C.
 View Solution
View SolutionQuestion 84
A cubical block of co-efficient of linear expansion αs is submerged partially inside a liquid of co-efficient of volume expansion γl. On increasing the temperature of the system by ΔT, the height of the cube inside the liquid remains unchanged. Find the relation between αsandγl. View SolutionQuestion 85
One end of a rod of length L and crosssectional area A is kept in a furnace at temperature T1. The other end of the rod is kept at a temperature T2. The thermal conductivity of the matrieal of the rod is K and emissivity of the rod is e. It is gives that T!=Ts+ΔT, where ΔT<<Ts,Ts is the temperature of the surroundings. If ΔT∝(T1−T2) find the proportional constant, consider that heat is lost only by rediation at the end where the temperature of the rod is T1.
 View Solution
View SolutionQuestion 86
A metal of mass 1 kg at constant atmospheric pressure and at initial temperature 20∘C is given a heat of 20000J. Find the following
(a) change in temperature,
(b) work done and
(c) change in internal energy.
(Given, specific heat =400J/kg−∘C, coefficient of cubical expansion, γ=9×10−5/∘C, density ρ=9000kg/m3, atmospheric pressure =105N/m2)View Solution
