Some water at 0∘C is placed in a large insulated enclosure (vessel). The water vapour formed is puped out continuously. What fraction of the water will ultimately freeze, if the latent heat of vapourization is seven times the latent heat of fusion?
To solve the problem, we need to analyze the heat exchange that occurs when water at 0°C is allowed to freeze while water vapor is continuously removed.
1. Understand the Given Information:
- Let Lf be the latent heat of fusion (the heat required to freeze water).
- Let Lv be the latent heat of vaporization (the heat required to vaporize water).
- It is given that Lv=7Lf.
- Let m be the total mass of water initially present.
- Let mi be the mass of water that ultimately freezes.
2. Heat Released by Freezing Water:
- When mi mass of water freezes, it releases heat equal to:
Qreleased=mi⋅Lf
3. Heat Absorbed by Remaining Water:
- The remaining mass of water after freezing is m−mi.
- This remaining mass absorbs the heat to vaporize, which is given by:
Qabsorbed=(m−mi)⋅Lv
4. Setting Up the Energy Balance:
- Since the heat released by the freezing water is equal to the heat absorbed by the remaining water, we can set up the equation:
mi⋅Lf=(m−mi)⋅Lv
5. Substituting Lv:
- Substitute Lv=7Lf into the equation:
mi⋅Lf=(m−mi)⋅(7Lf)
6. Canceling Lf:
- Since Lf is common on both sides, we can cancel it out (assuming Lf≠0):
mi=7(m−mi)
7. Expanding and Rearranging:
- Expanding the right side gives:
mi=7m−7mi
- Rearranging terms leads to:
mi+7mi=7m
8mi=7m
8. Finding the Fraction:
- Dividing both sides by 8 gives:
mi=78m
- Therefore, the fraction of water that ultimately freezes is:
mim=78
Final Answer:
The fraction of water that will ultimately freeze is 78.
- Let Lf be the latent heat of fusion (the heat required to freeze water).
- Let Lv be the latent heat of vaporization (the heat required to vaporize water).
- It is given that Lv=7Lf.
- Let m be the total mass of water initially present.
- Let mi be the mass of water that ultimately freezes.
- When mi mass of water freezes, it releases heat equal to:
Qreleased=mi⋅Lf
- The remaining mass of water after freezing is m−mi.
- This remaining mass absorbs the heat to vaporize, which is given by:
Qabsorbed=(m−mi)⋅Lv
- Since the heat released by the freezing water is equal to the heat absorbed by the remaining water, we can set up the equation:
mi⋅Lf=(m−mi)⋅Lv
- Substitute Lv=7Lf into the equation:
mi⋅Lf=(m−mi)⋅(7Lf)
- Since Lf is common on both sides, we can cancel it out (assuming Lf≠0):
mi=7(m−mi)
- Expanding the right side gives:
mi=7m−7mi
- Rearranging terms leads to:
mi+7mi=7m
8mi=7m
- Dividing both sides by 8 gives:
mi=78m
- Therefore, the fraction of water that ultimately freezes is:
mim=78
The fraction of water that will ultimately freeze is 78.
Topper's Solved these Questions
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Exercise 1.1
23 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Exercise 1.2
22 Videos
- BASIC MATHEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - BASIC MATHEMATICSEXERCISE - Exercise 2.6
20 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - INTEGER_TYPE
1 Video
Similar Questions
A thermal insulated vessel contains some water at 0∘C. The vessel is connected to a vaccum pump to pum out water vapour. This results in some water getting frozen. It is given latent heat of vaporization of water at 0∘C=21×105J/kg and latent heat of freezing of water =3.36×105J/kg. the maximum percentage amount of water vapour that will be solidified in this manner will be:
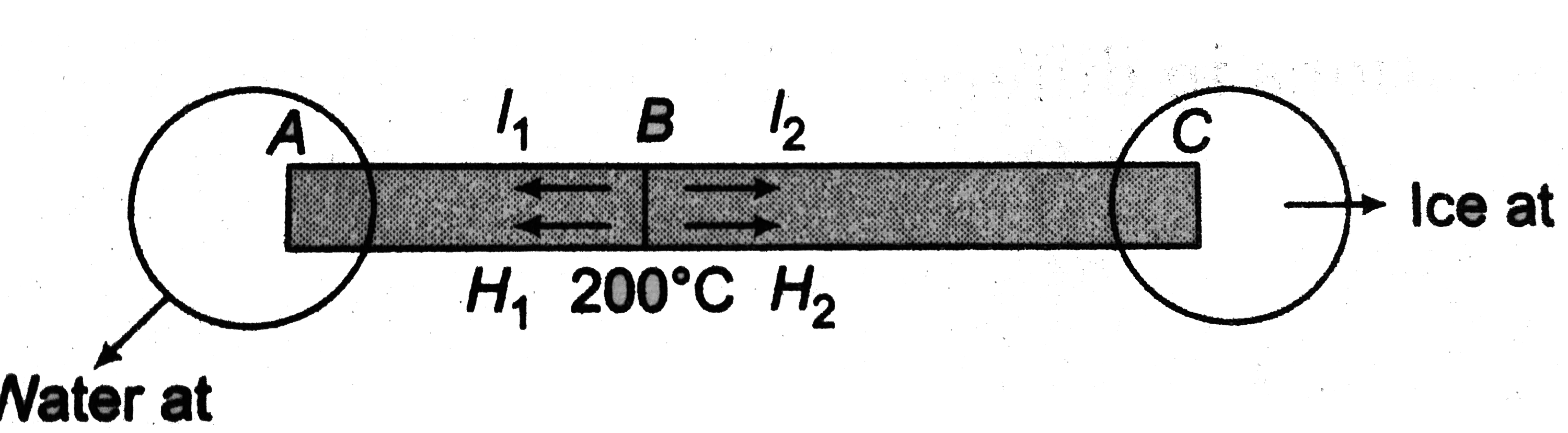
View SolutionB point of the rod shown in figure is maintained at 200∘C. At left end A, there is water at 100∘C and at right end C there is ice at 0∘C. Heat currents H1andH2 will flow on both sides. Due to H1, water will convert into steam and due to H2 ice will be melted. If latent heat of vaporization is 540cal/g and latent heat of fusion is 80cal/g then neglecting the radiation losses find l1l2 so that rate of melting of ice is two times the rate of conversion of water into stream.
 .
.
View Solution
Knowledge Check
The specific latent heat of fusion of water is :
A80 cal g−1B2260 J g−1C80 J g−1D336 J kg−1
A thermally isolated vessel contains 100g of water at 0∘C. When air above the water is pumped out, some of the water freezes and some evaporates at 0∘C itself. Calculate the mass of the ice formed such that no water is left in the vessel. Latent heat of vaporization of water at 0∘C=2.10×106J/kg and latent heat of fusion of ice =3.36×105J/kg.
View SolutionA thermally insulated vessel contains 150g of water at 0∘C. Then the air from the vessel is pumped out adiabatically. A fraction of water turms into ice and the rest evaporates at 0∘C itself. The mass of evaporated water will be closest to :
(Latent heat of vaporization of water =2.10×106jkg−1 and Latent heat of Fusion of water =3.36×105jkg−1)
View SolutionA vessel with 100 g of water at a temperature of 0∘C is suspended in the middle of a room. In 15 minutes the temperature of the water rises to 1.8∘C. When ice equal in weight of the water is placed in the same vessel, it melts during 10 hours. using appropriate appropriate approximations, estimate the latent heat of fusio of ice in cal/g. if the known alue of latent heat of fusion of ice is 80 cal/g, obtain the difference in the two values in cal/g and report this as your answer.
View SolutionWater at 0∘C was heated until it started to boil and then until it all changed to steam. The time required to heat water from 0∘C to 100∘C is 5 min and the time to change boiling water to steam is 28 minutes. If the flame supplied heat at a constant rate, the specific latent heat of vaporization of water (neglecting heat losses, container etc. is (in J/g). (specific heat of water s =4.2J/g )
View SolutionHow should 1kg of water at 50∘C be divided in two parts such that if one part is turned into ice at 0∘C. It would release sufficient amount of heat to vapourize the other part. Given that latent heat of fusion of ice is 3.36×105J/Kg. Latent heat of vapurization of water is 22.5×105J/kg and specific heat of water is 4200J/kgK.
View Solution1 g ice at 0∘C melts to form 1 g water at 0∘C. State whether the latent heat is absorbed or given out by ice.
View SolutionA small quantity mass m, of water at a temperature θ(in ∘C) is poured on to a larger mass M of ice which is at its melting point. If c is the specific heat capacity of water and L the specific heat capacity of water and L the specific latent heat of fusion of ice, then the mass of ice melted is give by
View Solution