In the shown arrangement, both the spring are in their natural lengths. The coefficient of friction between m2 and m1 is μ. There is no friction between m1 and the surface. If the blocks are displaced slightly, they together perform simple harmonic motion. Obtain

(a) Frequency of such oscillations.
(b) The condition if the friction force on clock m2 is to act in the direction of its displacement from mean position.
( c) If the condition obtained in (b) is met, what can be maximum of their oscillations ?
The correct Answer is:12π√K1+K2m1+m2
a. For the oscillation of the blocks together, the equivalent, force constant equals K1+K2 and hence the frequency
A=12π√K1+K2m1+m2
b. Assuming that the block (m1+m2) are displaced towards right, the various forces (except the frictional force) on m2, in the reference frame of m1 are shown in the following free body diagram.
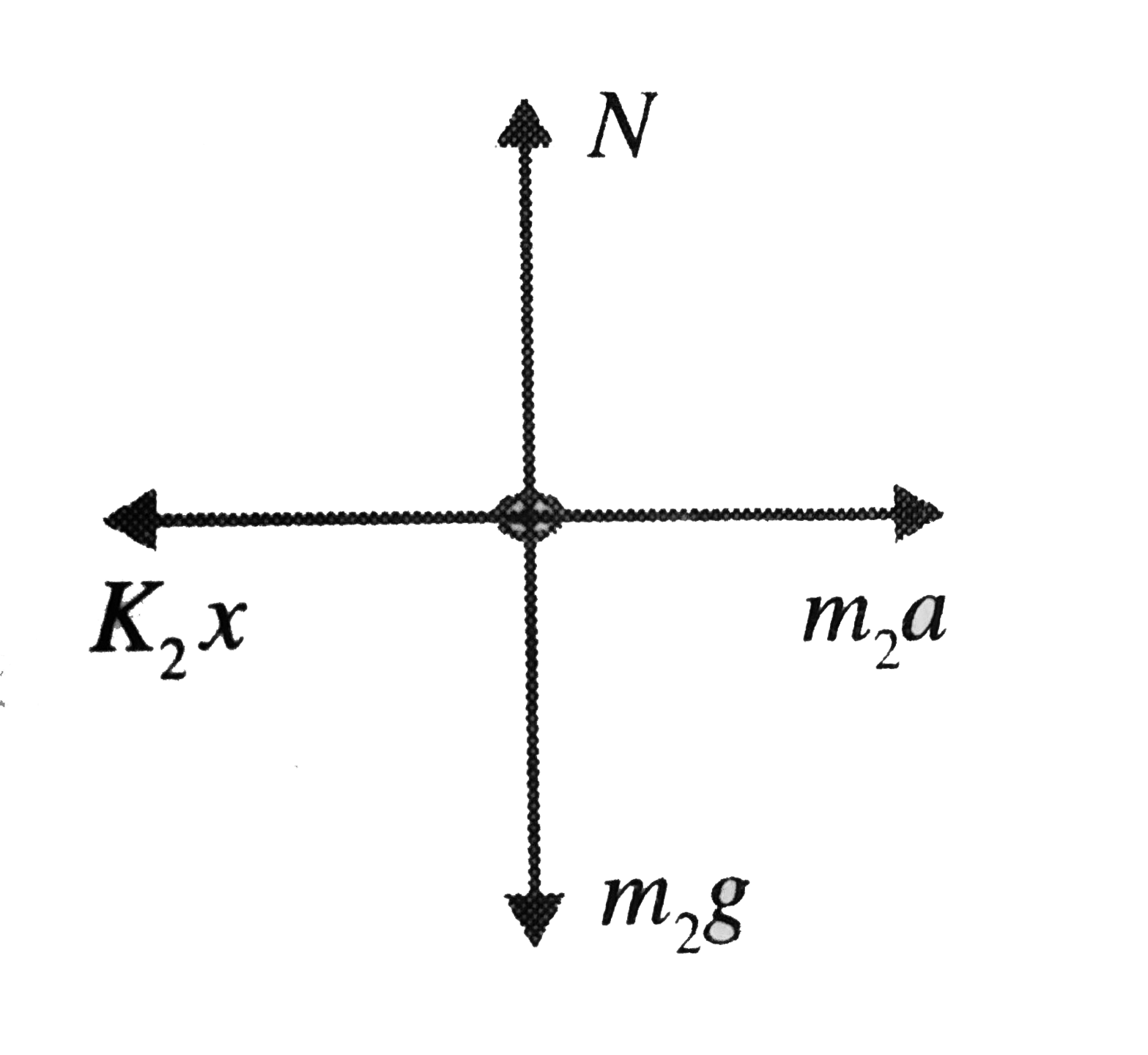
where a=(K1+K2xm1+m2)
For the frictional force to act on m2 in the direction of its displacement
K2x>m2[K1+K2m1+m2]x
m1K2+m2K2−m2K2>0
m1K2−m2K1>0
m1m2>K1K2
The above inequality is in the desired condition.
c.
Assuming m1m2>K1K2 the FBD of m2 with m1 andm2
together displacement towardsright can be shown as
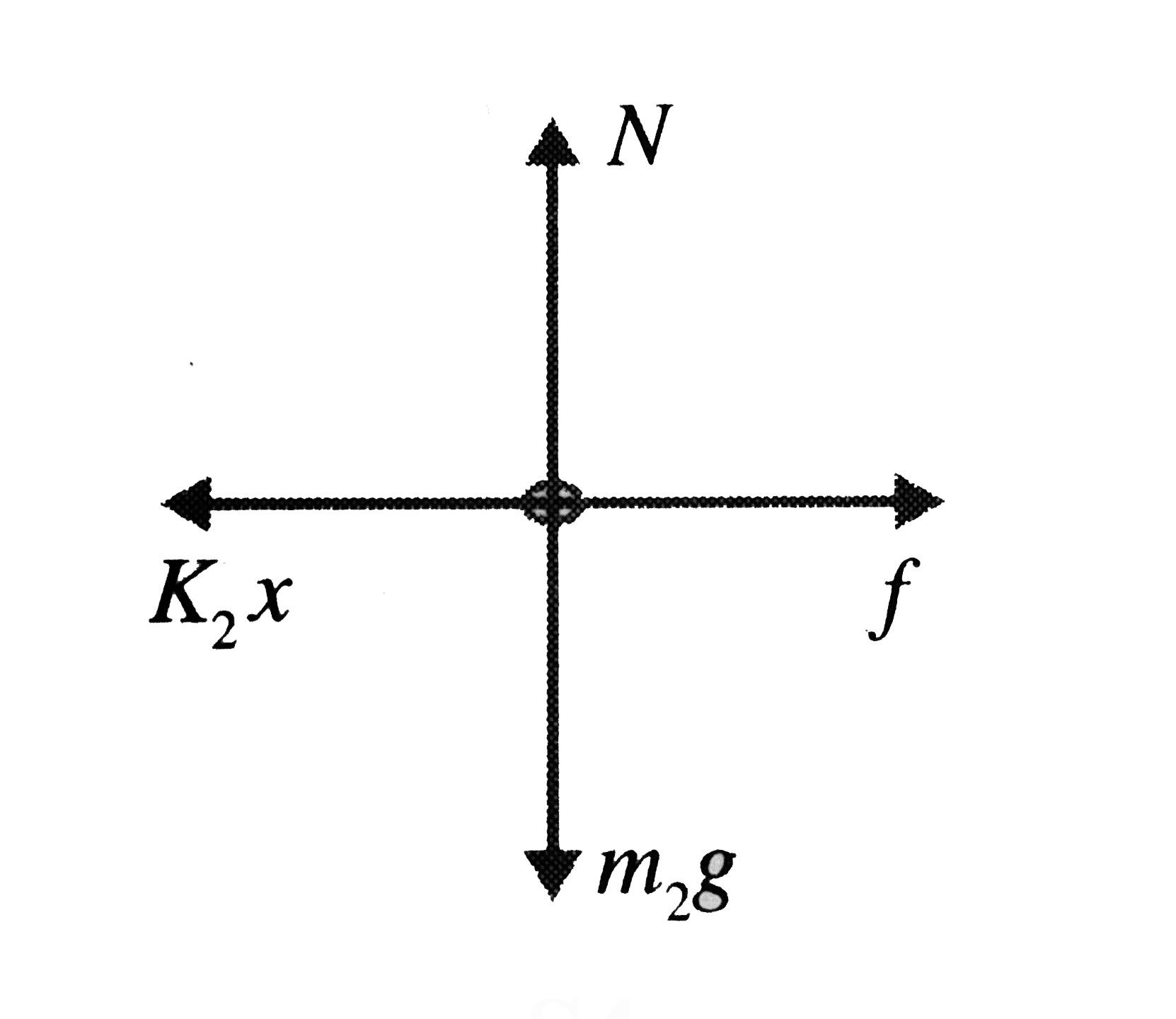
If A be the amplitude of oscillation of m2K2A−f=m2ω2A (for the exterme position)
f=K2A−m2ω2A⇒f=A(K2−m2ω2)
f≤μm2g⇒μm2g≥A(K2−m2ω2)
A≤μm2g(K2−m2ω2)⇒Amax=(μm2g(K2−m2ω2))
Here ω2=m(K1+K2)(m1+m2),Amax=(μm2g(m1+m2)m1K2−m2K1)
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Single Correct
107 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Multiple Correct
35 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Exercise 4.2
23 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
Similar Questions
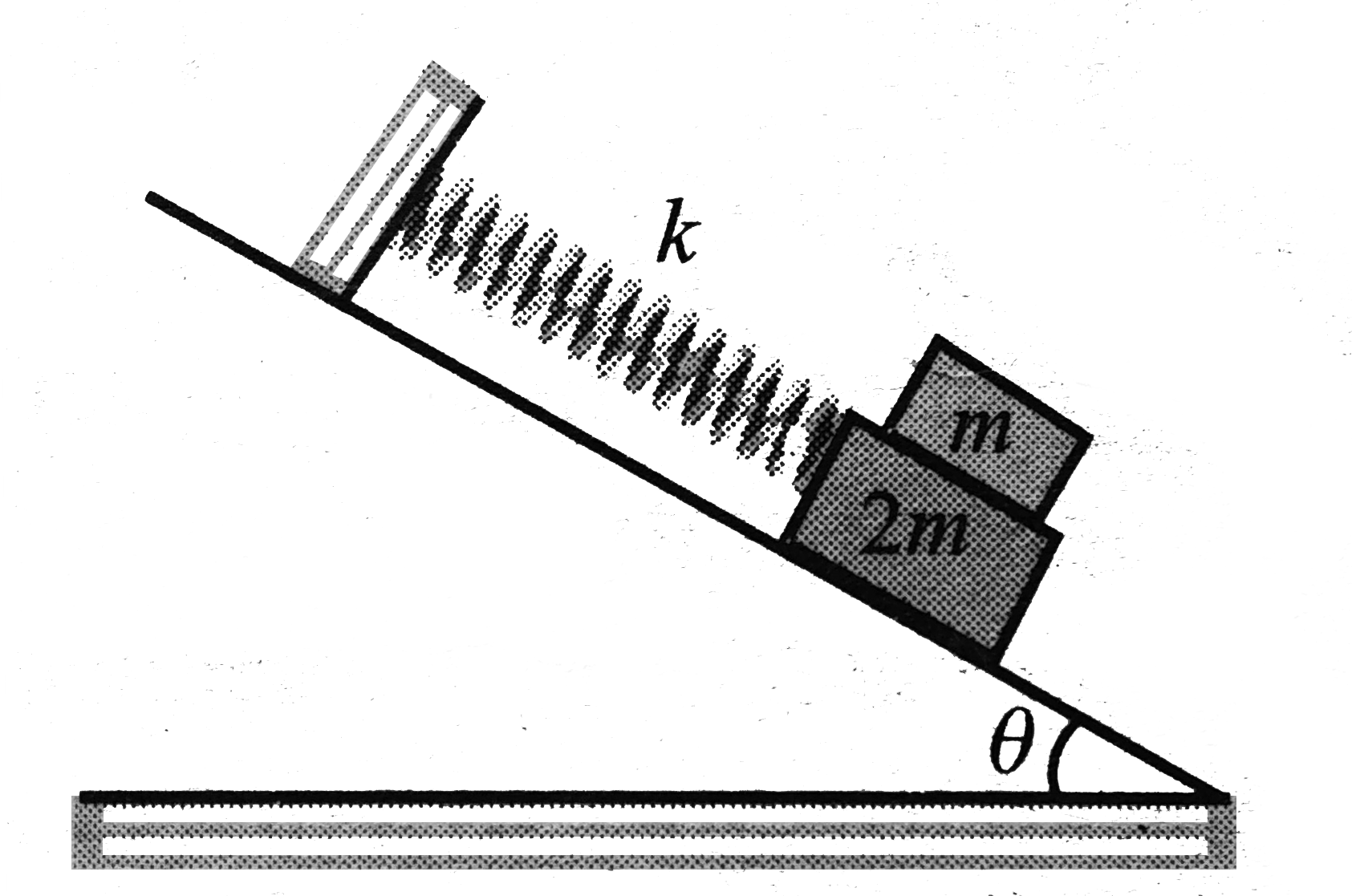
The coefficient of friction between block of mass m and 2m is μ=2tanθ. There is no friction between block of mass 2 m and inclined plane. The maximum amplitude of the two block system for which there is no relative motion between both the blocks is
View Solution
The coefficient of friction between block of mass m and 2m is μ=2tanθ. There is no friction between block of mass 2 m and inclined plane. The maximum amplitude of the two block system for which there is no relative motion between both the blocks is
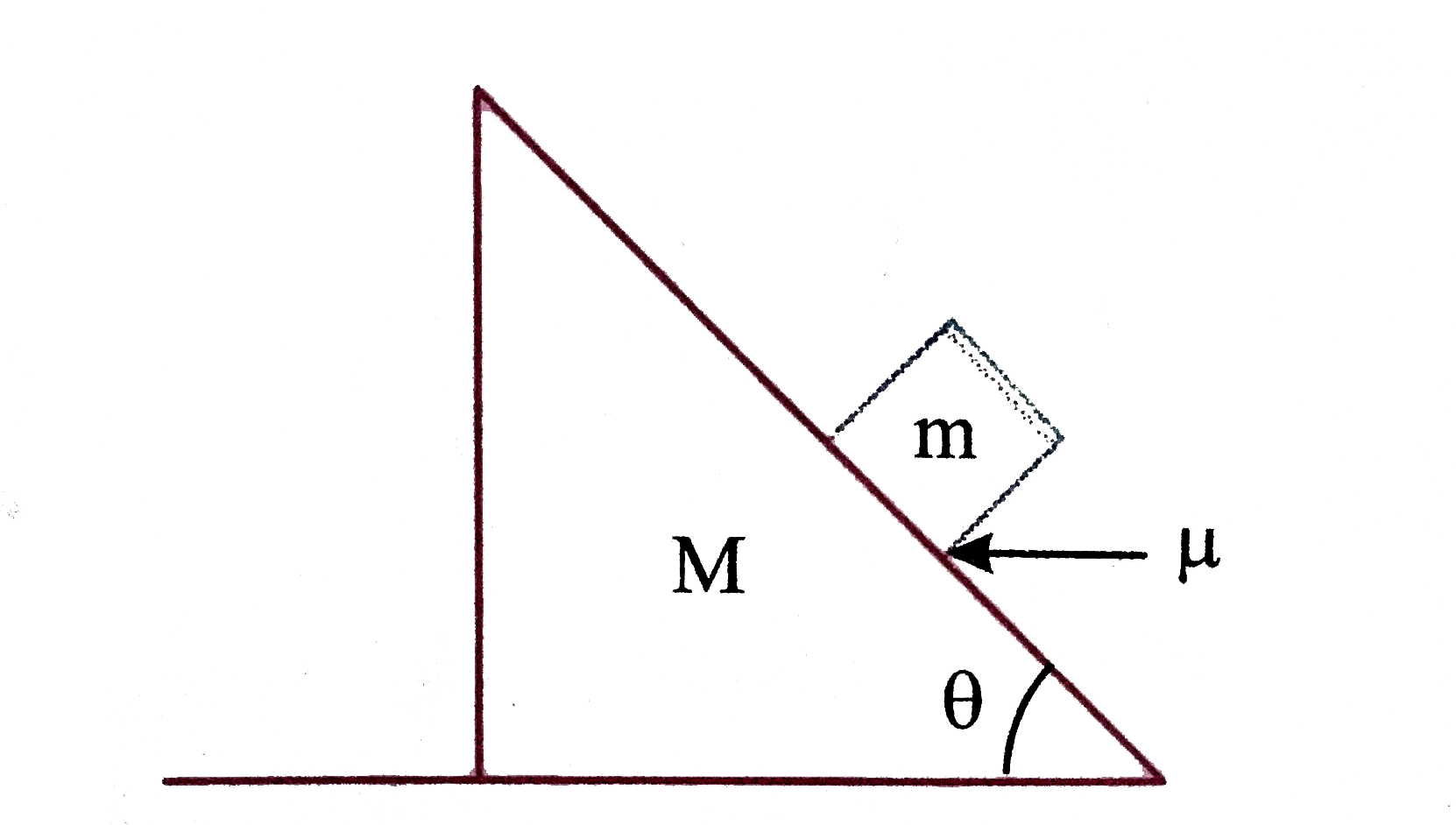
View SolutionThe coefficient of friction between the block A of mass m and the triangular wedge B of mass M is μ. There in no friction between the wedge and the plane if the system (block A+ wedge B) is released so that there is no stiding between A and B find the inclination θ

View SolutionCalculate angle of friction between wedge and block system is at rest M coefficient of friction between wedge and block.
View SolutionIn the pulley arrangement shown in Fig the pulley p2 is movable .Assuming the coefficient of friction between m and surface to be μ the minimum value of M for which m is at rest is

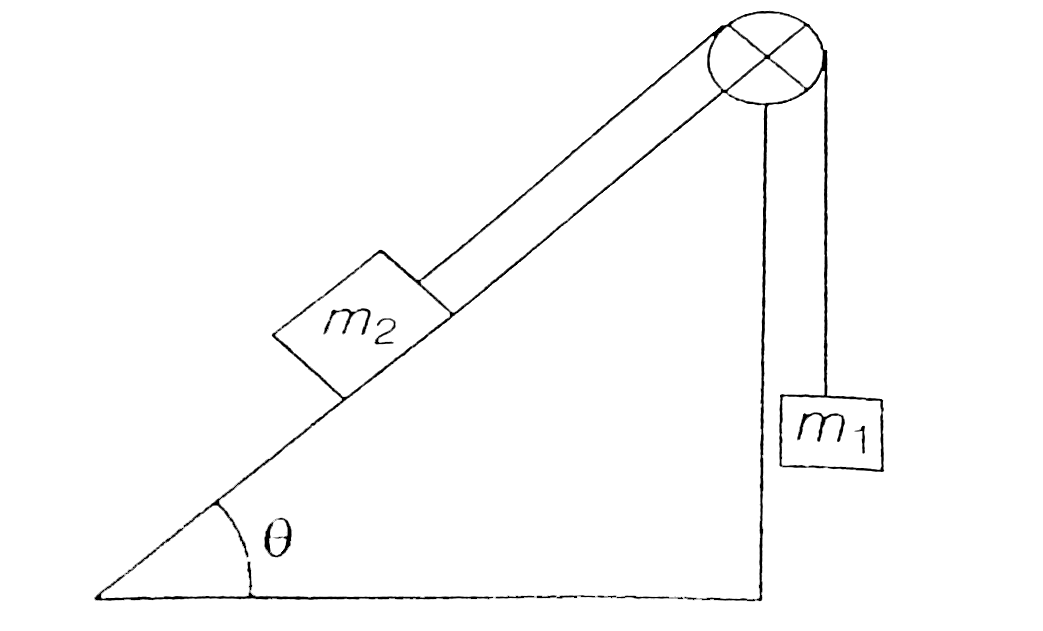
View SolutionIn the figure shown if coefficient of friction is μ, then m2 will start moving upwards if
View SolutionA block of mass m is moving on a rough horizontal surface. μ is the coefficient of kinetic friction between the block and the surface. What is the net force exerted by the surface on the block?
View SolutionA block of mass'm' is resting on the floor of a lift. The coefficient of friction between the block and the floor is μ. When the lift is falling freely, the limiting frictional force between block and surface is
View SolutionFor the arrangement shown in the figure the coefficient of friction between the two blocks is μ. If both the blocks are identical and moving ,then the acceleration of each block is

View SolutionA block of mass m is placed behind in contact with vertical side of M as shown in the figure. The coefficient of static friction between m and M in μ. The least horizontal force with which m can be pushed so that the two blocks move together is (neglect friction between M and ground).
View Solution
