A particle of mass 2kg is moving of a straight line under the actin force F=(8−2x)N. It is released at rest from x=6m.
a. Is the partical moving simple harmonically.
b.Find the equilibrium position of the particle.
c. Write the equation of motion of the partical.
d. Find the time period of SHM.
The correct Answer is:a. Yes
b. x=4m
c.x=4+2cost
d.2πsec
f=8−2x
or F=−2(x−4)
For equilibrium position F=0
⇒x=4 is equilibrium position
Hence the motion of the partuical is SHM with force canstant 2 and equilibrium positionx=4 .
a. Yes, motion is SHM.
b. Equilibrum position is x=4
c. At x=6m. Partical is rest ia at rest , i. e. it is one of the the extreme position.
Hence amplitude A is 2 m and initial partical is at the exterme position.
Therefore, equation of SHM can be written as
x−4=2cosωt,whereω=√km=√22=1
i.e. x=4+cost
d. Time period T=2πω=2πsec.
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Single Correct
107 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Multiple Correct
35 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Exercise 4.2
23 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
Similar Questions
A particle of mass 2kg is moving of a straight line under the action of force F=(8−2x)N. It is released at rest from x=6m.
a. Is the particle moving simple harmonically.
b. Find the equilibrium position of the particle.
c. Write the equation of motion of the particle.
d. Find the time period of SHM.
View SolutionA particle of mass 2kg is moving on a straight line under the action of force F=(8−2x)N. It released at rest from x=6m.
(a) Is the particle moving simple harmonically.
(b) Find the equilibrium position of the particle.
(c) Write the equation of motionof the particle.
(d) Find the time period of SHM.
View SolutionA particle of mass 2kg is moving on a straight line under the action of force F=(8−2x)N. The particle is released at rest from x=6m. For the subsequnent motion(All the value in the right column are in their S.I. units)
_E01_071_Q01.png)
View SolutionThe potential energy U(x) of a particle moving along x - axis is given by U(x)=ax−bx2. Find the equilibrium position of particle.
View SolutionFor a particle performing SHM, equation of motion is given as d2dt2+9x=0. Find the time period
View SolutionFor a particle performing SHM, equation of motion is given as d2dt2+4x=0. Find the time period
View SolutionA particle of mass 2kg moves in simple harmonic motion and its potential energy U varies with position x as shown. The period of oscillation of the particle is

View SolutionA particle of mass 2kg moves in simple harmonic motion and its potential energy U varies with position x as shown. The period of oscillation of the particle is

View SolutionA particle executing simple harmonic motion has amplitude of 1m and time period 2s. At t=0, net force on the particle is zero. Find the equation of displacement of the particle.
View SolutionA particle of mass = 2kg moves in simple harmonic motion and its potential energy U varies with position x as shown. The period of oscillation of the particle is nπ5 second. Find value of n.
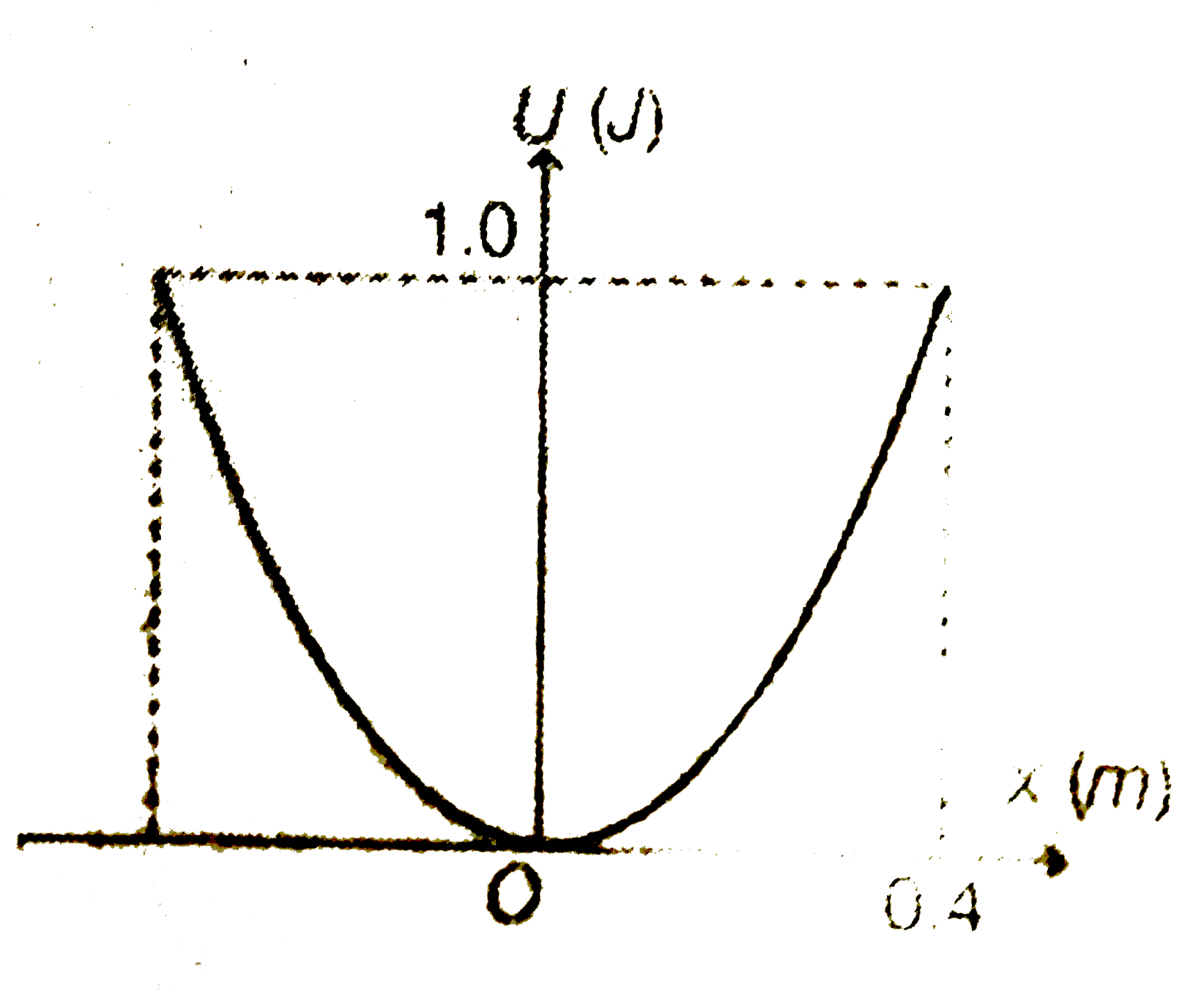
View Solution
