Question

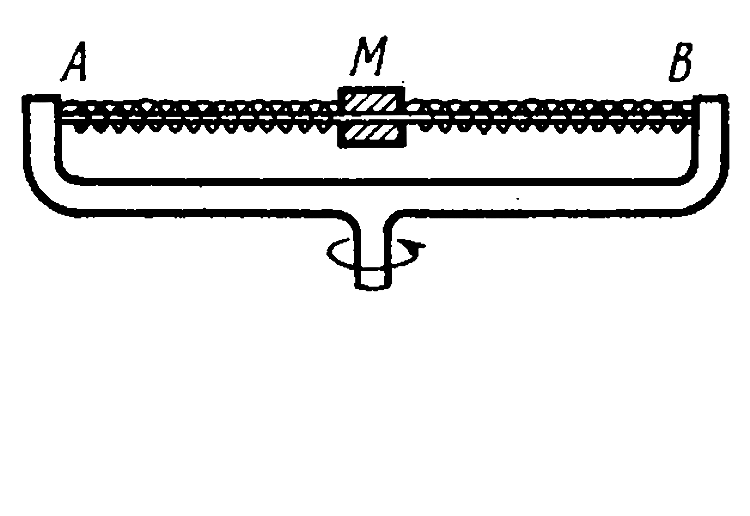
In the arrangement shown in figure the sleeve $M$ of mass $m=0.20kg$ is fixed between two identical springs whose combined stiffness is equal to $x=20N/m$. The sleeve can slide without friction over a horizontal bar $AB$. The arrrangement rotates with a constant angular velocity $\omega =4.4rad/s$ about a vertical axis passing through the middle of the bar . Find the period of small oscillations of the sleeve. At what values of $\omega$ will there be no oscillations of the sleeve ?

Answer

`2 pi sqrt((m)/(k - m omega^(2)))`

Explanation

We will analyse se the problem relative to the rotating bar AB. As the acceleration of bar is centripetaing , a pseudo force will act on sleeve away from the centre and will be of magnitude `m (omega^(2) x)`.
If the sleves is displaced by x, net force towards center

`F = kx - m omega^(2) x = (m - m omega^(2)) x`
`implies period = 2 pi sqrt((m)/(k - m omega^(2)))`
Note that if `k lt m omega^(2)`. there will be no oscillations of the sleves. It will rush to the point B if it is displaced slightly (for `k lt m omega^(2))`. or will remain in the displaced position `(for k = m omega^(2))`.