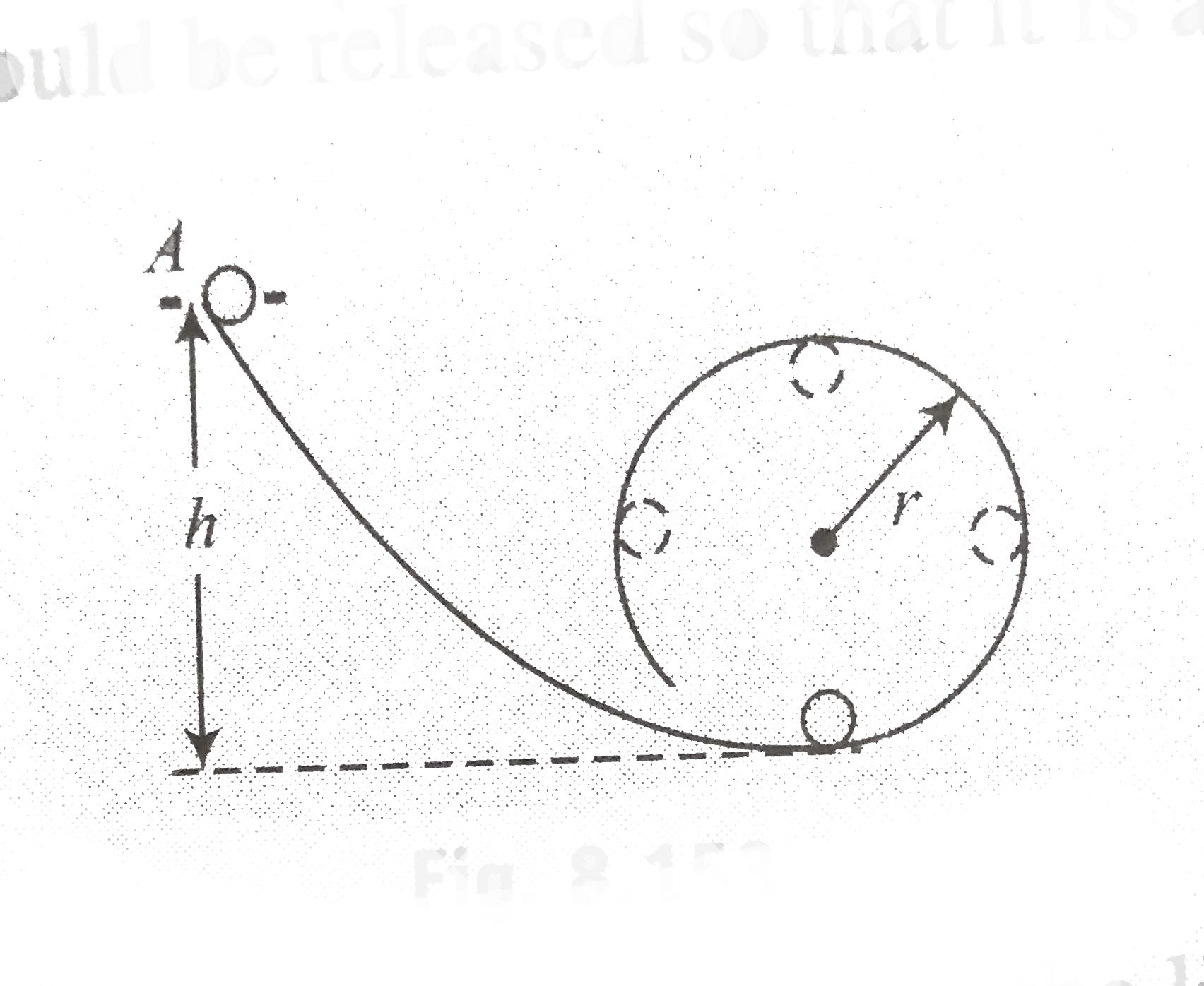Assertion And Reason from DC PANDEY ENGLISH CIRCULAR MOTION for Class 11
| Class 11 | PHYSICS |
| Chapter | CIRCULAR MOTION |
| DC PANDEY ENGLISH | Assertion And Reason |
| Medium | English |
| Academic Year | 2023-2024 |
Question 28
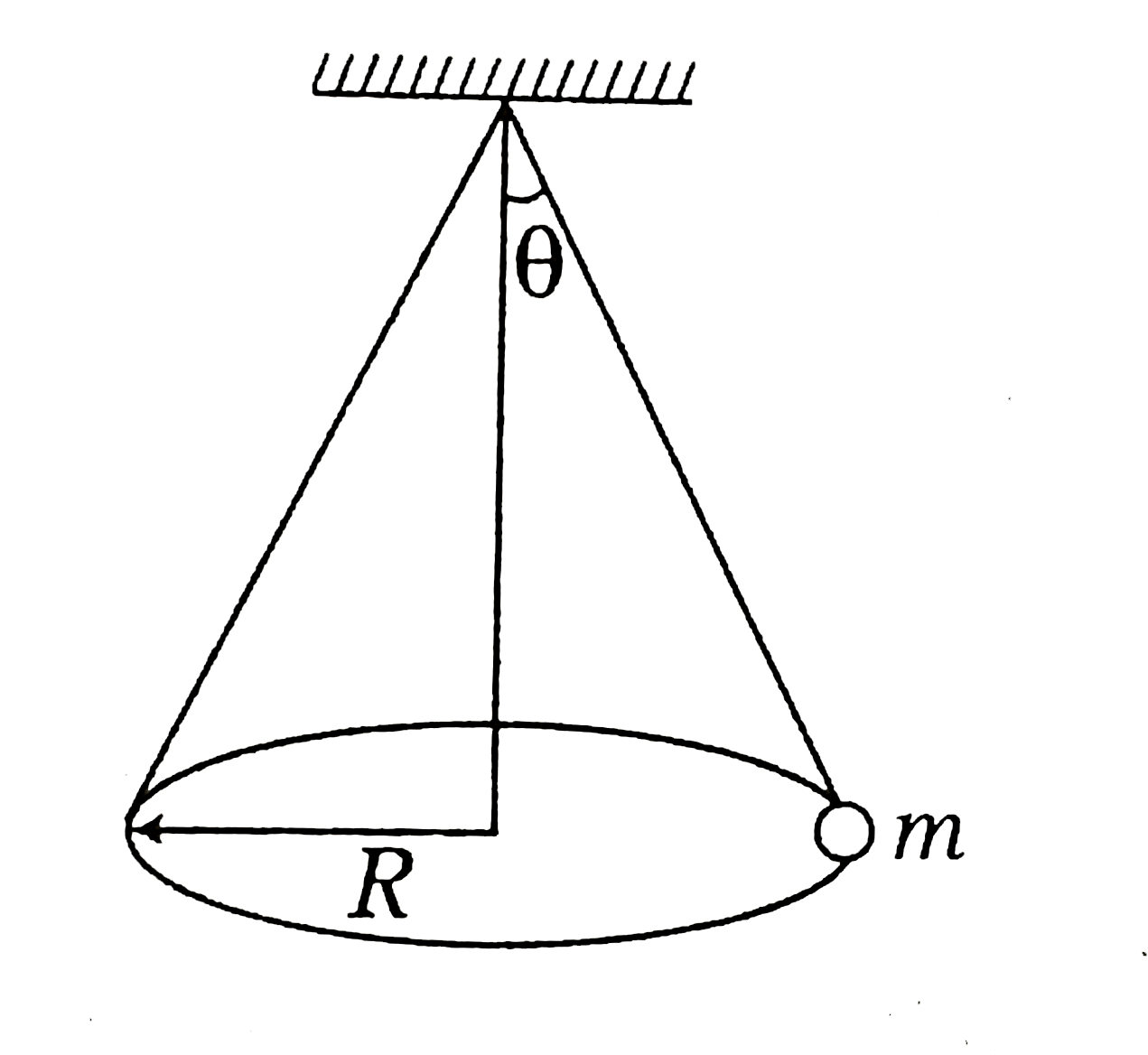
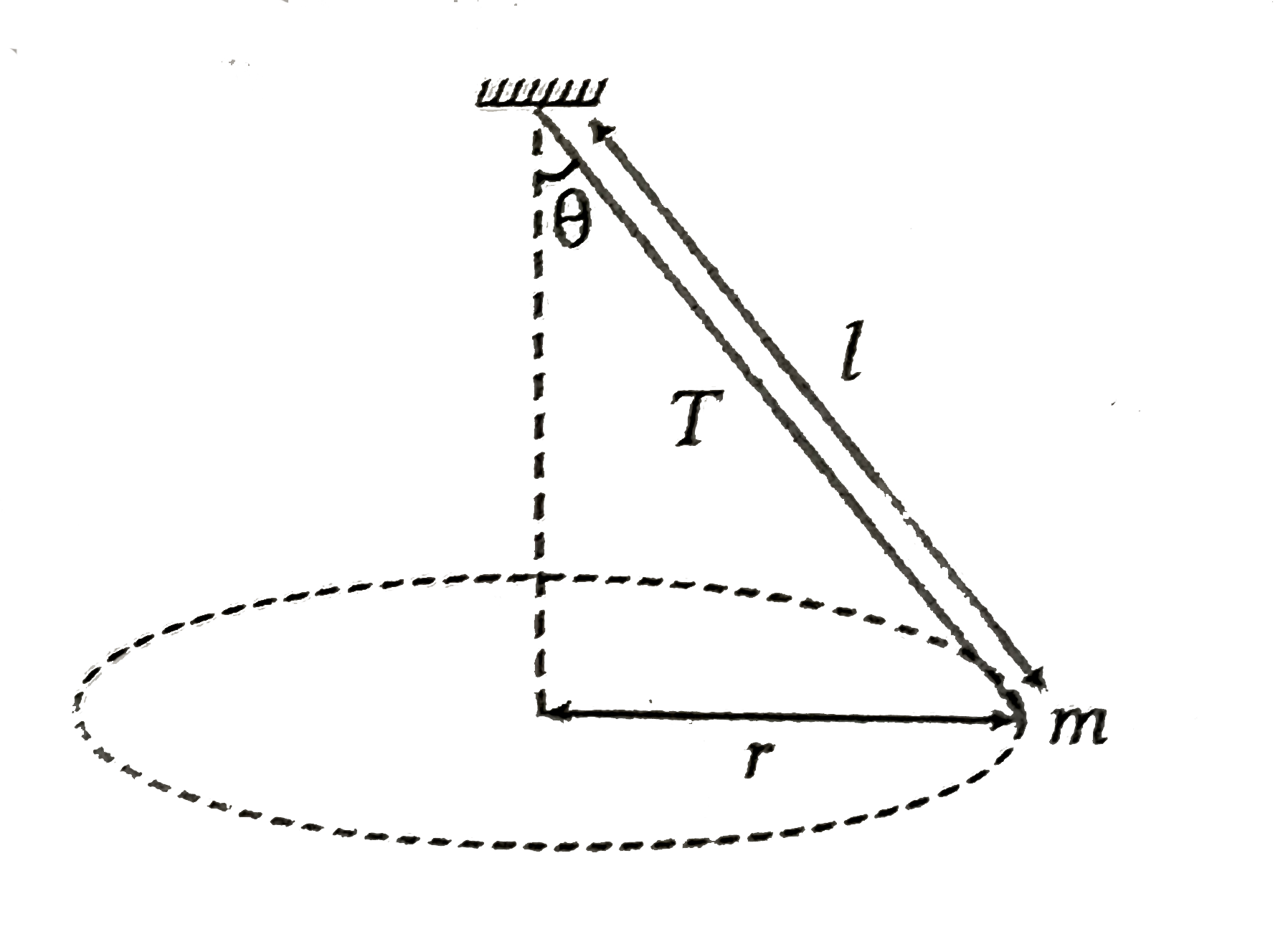
A mass of 100 gm is tied to one end of a string 2 m long. The body is revolving in a horizontal circle making a maximum of 200 revolutions per min. The other end of the string is fixed at the centre of the circle of revolution. The maximum tension that the string can bear is (approximately) View SolutionQuestion 32
A motor cyclist moving with a velocity of 72 km/hour on a flat road takes a turn on the road at a point where the radius of curvature of the road is 20 meters . The acceleration due to gravity is 10m/sec2. In order to avoid skidding, he must not bend with respect to the vertical plane by an angle greater than View SolutionQuestion 35
A person wants to drive on the vertical surface of a large cylindrical wooden 'well' commonly known as 'death well' in a circus. The radius of the well is R and the coefficient of friction between the tyres of the motorcycle and the wall of the well is u. The minimum speed the motor cyclist must have in order to prevent slipping should be -View SolutionQuestion 38
A stone of mass of 1 kg is tied to the end of a string 1 m long. It is whirled in a vertical circle. The velocity of the stone at the bottom of the circle is just sufficient to take it to the top of circle without slackening of the string. What is the tension in the string at the top of the circle? (Take, g =10 ms−2)View SolutionQuestion 69
A motor cyclist moving with a velosity of 72kmh−1 on a flat road takes a turn on the road at a point where the radius of curvature of the road is 20km. The acceleration due to gravity is 10ms−2. IN order to avoid skidding , he must not bend with respesct to the vertical plane by an angle greater then View SolutionQuestion 80
A mass is attached to the end of a string of length l which is tied to a fixed point O. The mass is released from the initial horizontal position of the string. Below the point O at what minimum distance a peg P should be fixed so that the mass turns about P and can describe a complete circle in the vertical plane?View SolutionQuestion 89
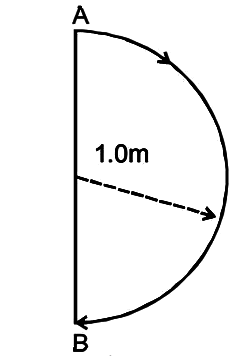
A cyclist starts from the center O of a circular park of radius 1km, reaches the edge P of the park, then cycles along the PQ circumference and returns to the center along OQ as shown in fig. If the round trip taken ten minute, the (a) net displacement, (b) average velocity and (c) average speed of the cyclists (in kilometer per hour) is
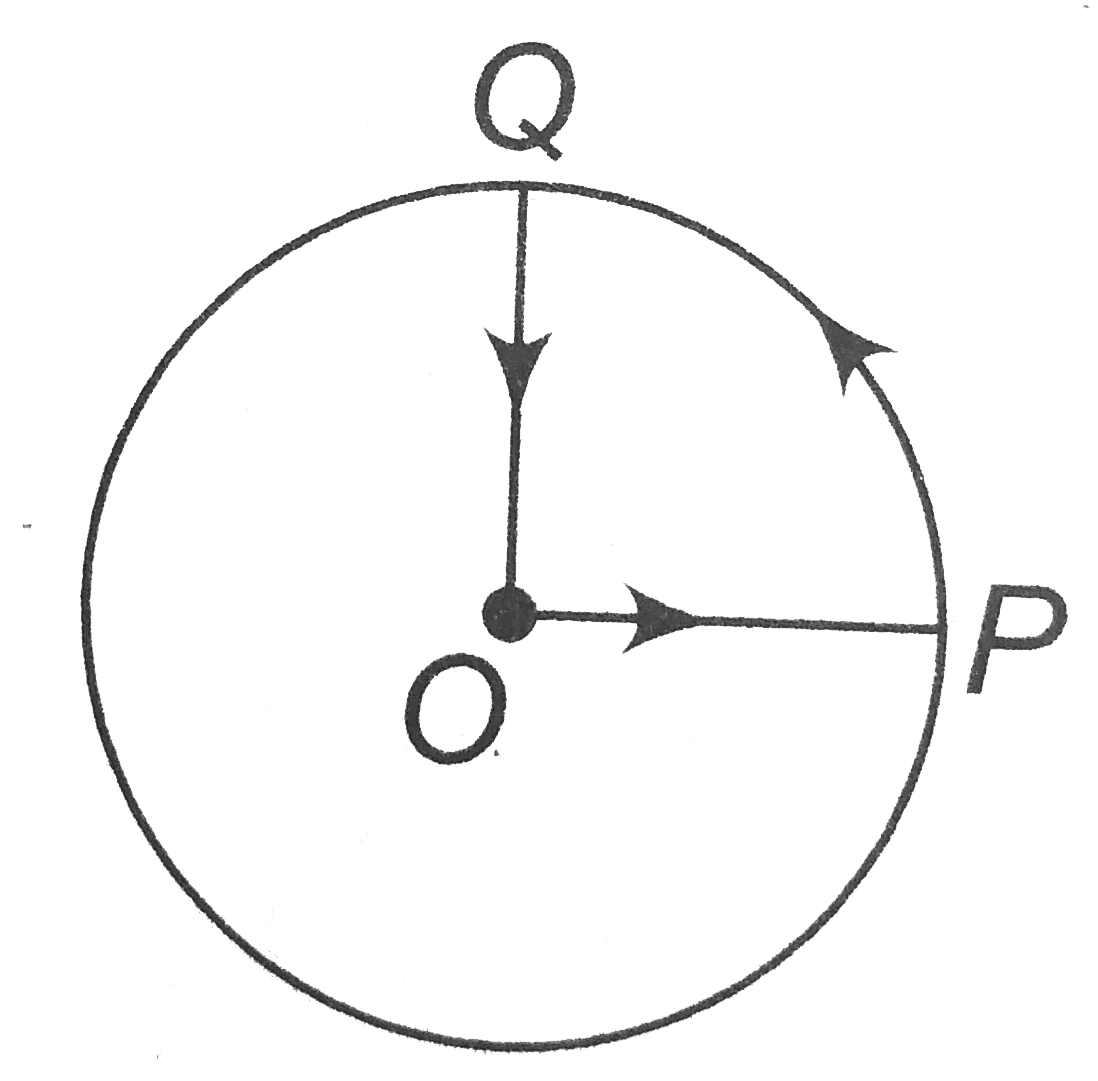 View Solution
View SolutionQuestion 90
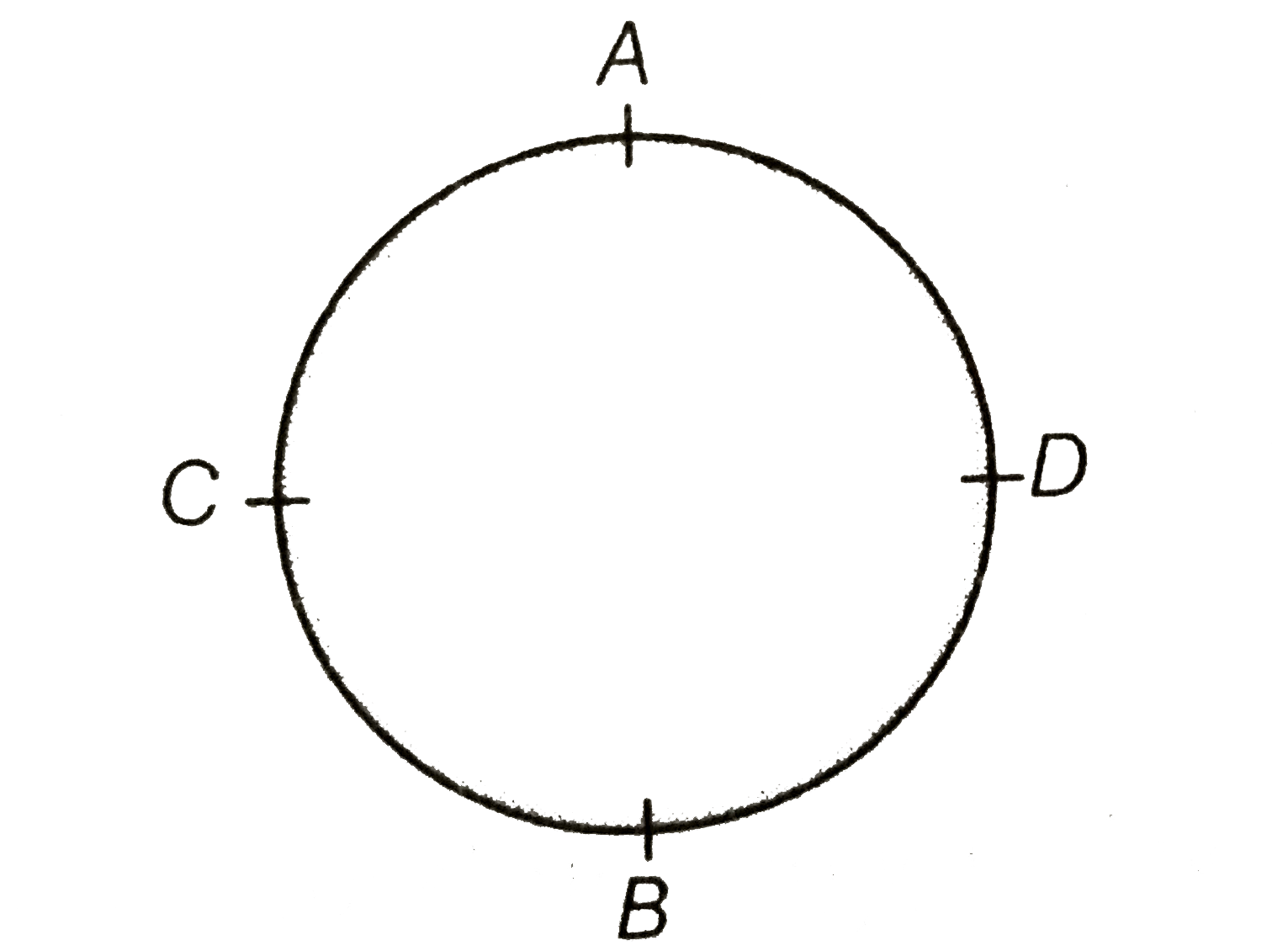
Three particles A, B and C move in a circle of radius r=1πm, in anti-clockwise direaction with speed 1ms−1,2.5ms−1 and 2ms−1 respectively. The initial position of A, B and C are as shown in figure.
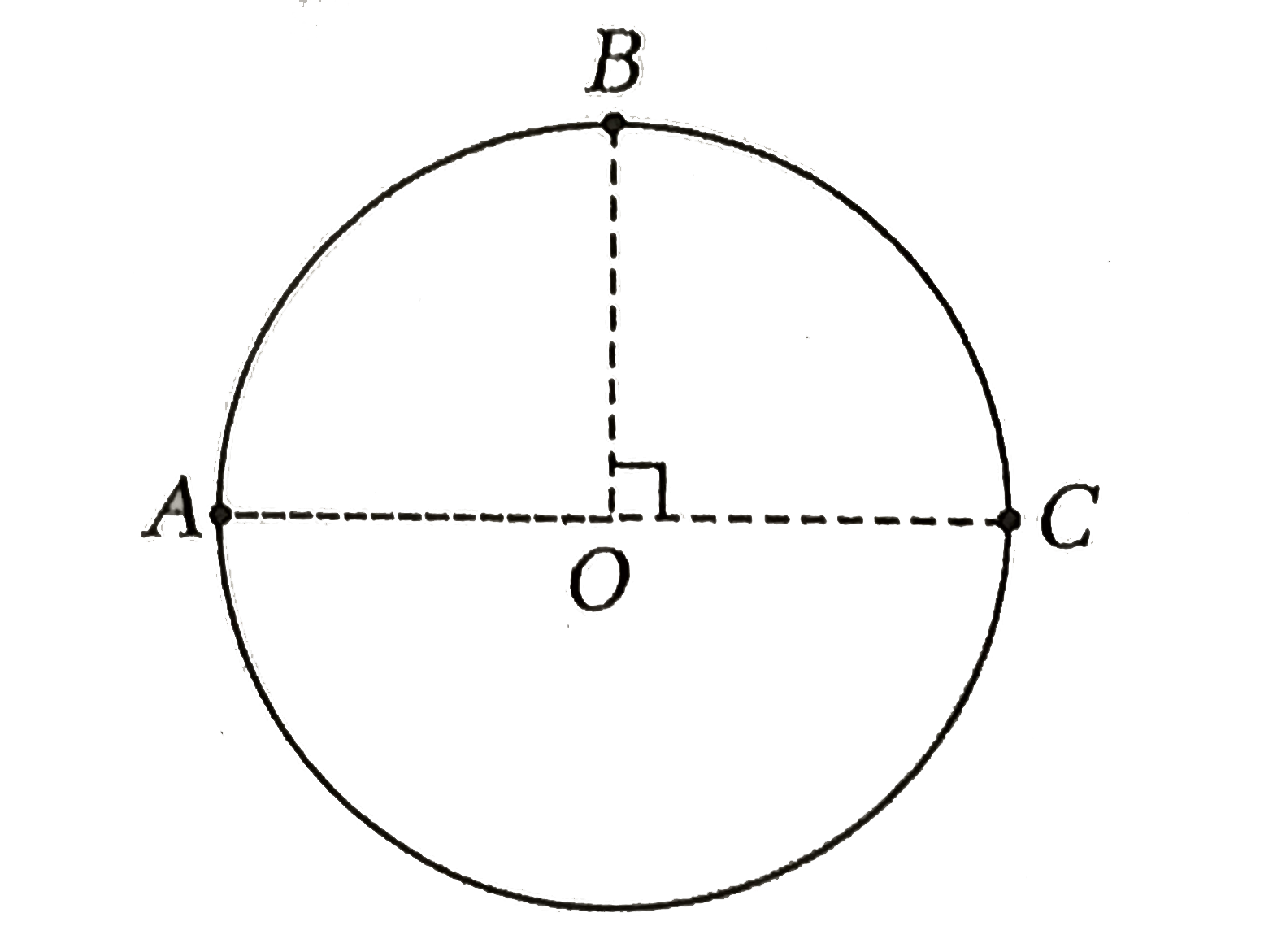
The ratio of distance travelled by B and C by the instant A, B and C meet for the first time is View SolutionQuestion 92
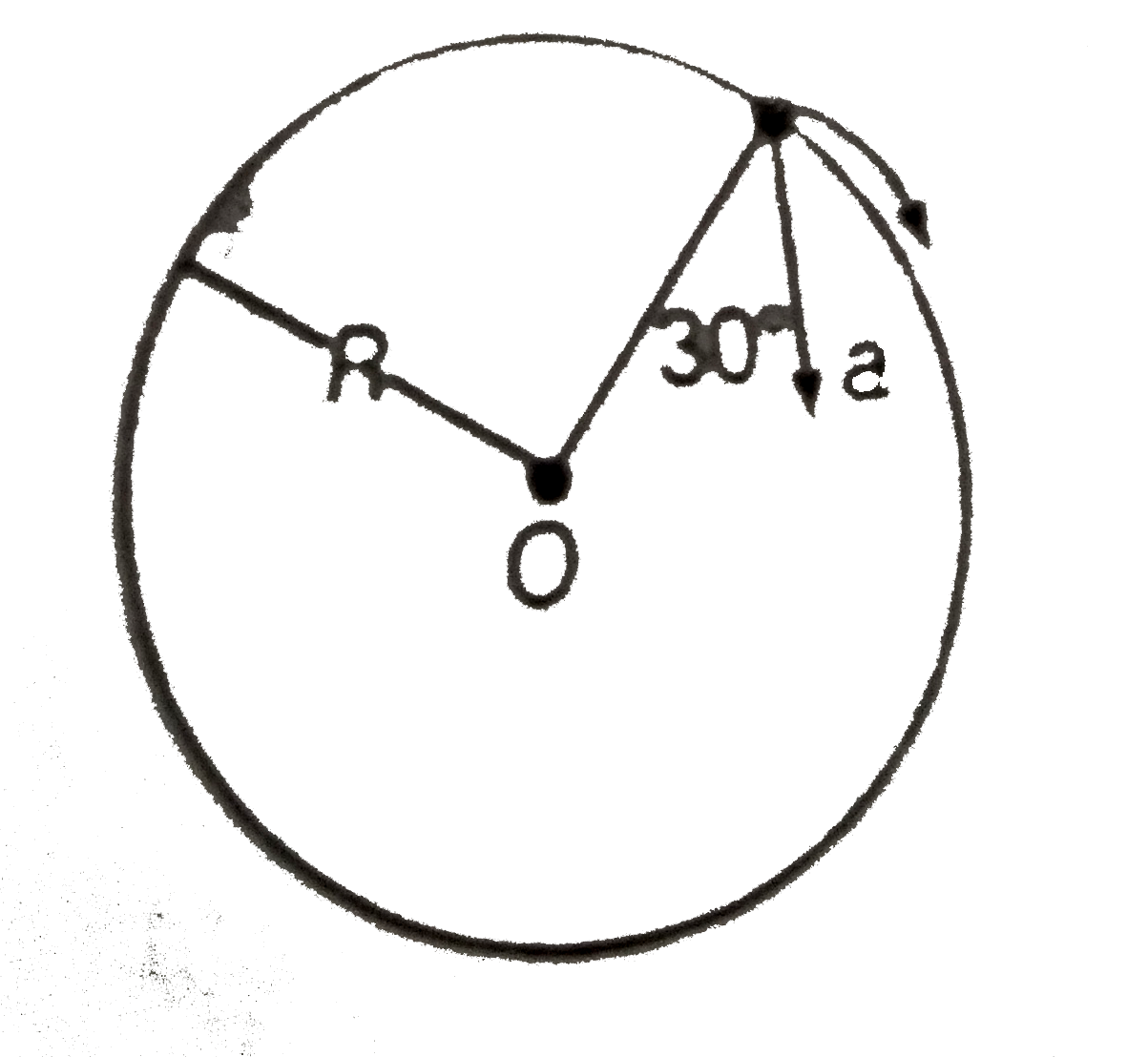
A boy whirls a stone of small mass in a horizontal circle of radius 1.5m and at height 2.9m above level ground. The string breaks and the stone flies off horizontally and strikes the ground after travelling a horizontal distance of 10m . What is the magnitude of the centripetal acceleration of the stone while in circular motion ? View SolutionQuestion 93
A stone tied to a string of length L is whirled in a vertical circle with the other end of the string at the centre. At a certain instant of time the stone is at lowest position and has a speed u . Find the magnitude of the change in its velocity as it reaches a position, where the string is horizontal. View SolutionQuestion 106
Two bodies of masses m and 4m are attached to a light string as shown in figure. A body of mass m hanging from string is executing oscillations with angular amplitude 60∘, while other body is at rest on a horizontal surface. The minimum coefficient of friction between mass 4m and the horizontal surface is (here pulley is light and smooth)
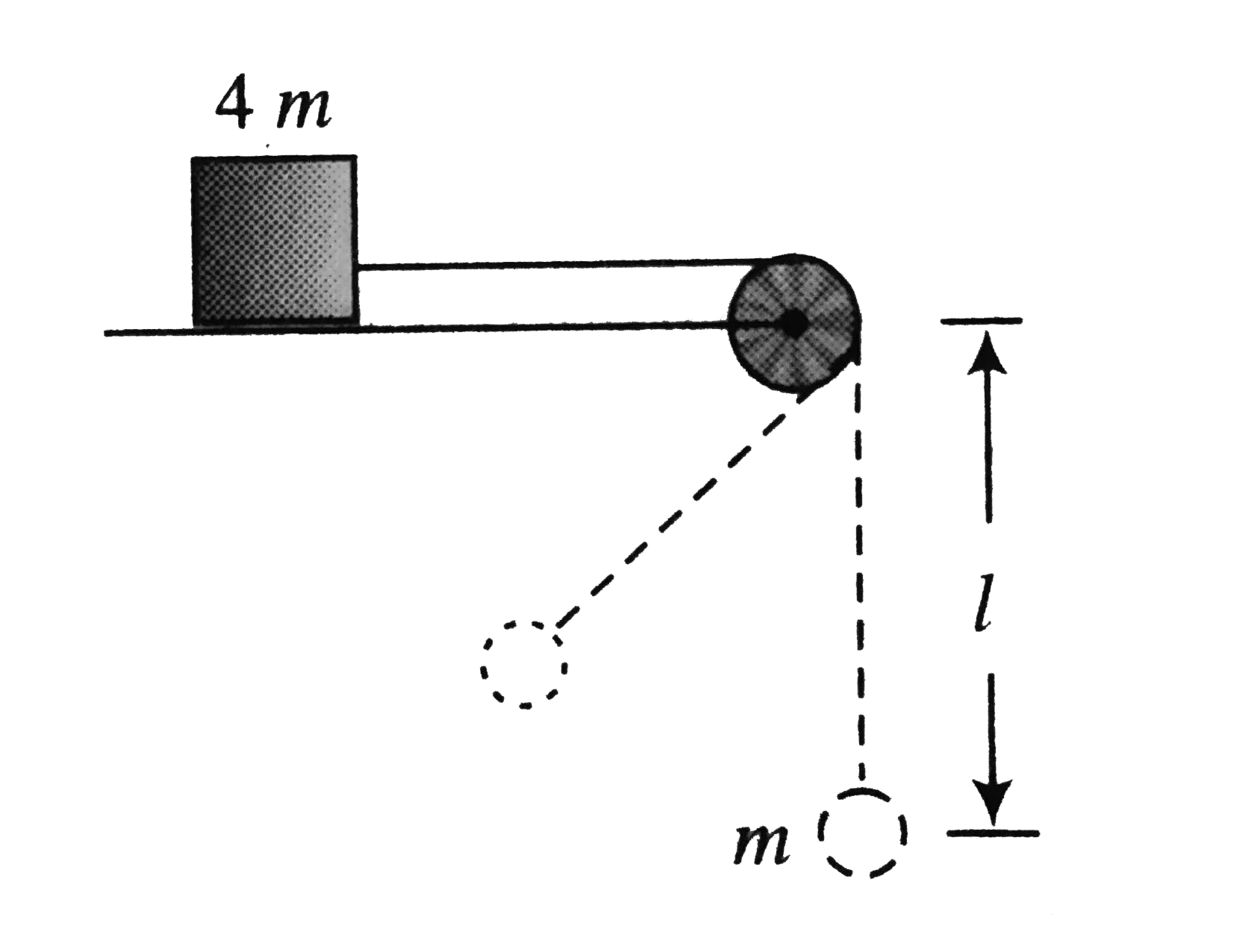 View Solution
View SolutionQuestion 107
A bullet of mass m moving with a horizontal velocity u strikes a stationary wooden block of mass M suspended by a string of length L = 50 cm. The bullet emerges out of the block with speed u4. If M = 6 m, minimum value of u so that the block can complete the vertical circle (take, g = 10 ms−2)View SolutionQuestion 114
On a frictionless horizontal surface , assumed to be the x−y plane , a small trolley A is moving along a straight line parallel to the y−axis ( see figure) with a constant velocity of (√3−1)m/s . At a particular instant , when the line OA makes an angle of 45(∘) with the x− axis , a ball is thrown along the surface from the origin O. Its velocity makes an angle ϕ with the x− axis and it hits the trolley .
(a) The motion of the ball is observed from the frame of the trolley . Calculate the angle θ made by the velocity vector of the ball with the x−axis in this frame .
(b) Find the speed of the ball with respect to the surface , if ϕ=(4θ)/(3).
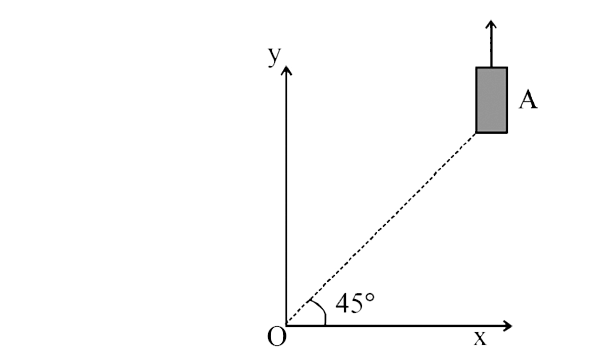 View Solution
View SolutionQuestion 117
STATEMENT -1 : In non - uniform circular motion acceleration of a particles is along the tangent of the circle .
STATEMENT -2 : In uniform circular motion acceleration of a particle is zero .
STATEMENT -3 : In no - uniform circular motion acceleration of a particle is towards the centre of the circle.View SolutionQuestion 126
Assertion A ball tied by thread is undergoing circular motion (of radius R) in a vertical plane. (Thread always remains in vertical plane). The difference of maximum and minimum tension in thread is independent of speed (u) of ball at the lowest position (u>√5gR).
Reason For a ball of mass m tied by thread undergoing vertical circular motion (of radius R), difference in maximum and minimum magnitude of centripetal aceleraion of the ball is independent of speed (u) of ball at the lowest position (ugr√5gR)).View SolutionQuestion 127
Assertion One end of a massless rod of length l is hinged so that it is free to rotate in vertical plane about a horizontal axis. If a particle is attached to the other end of the rod, then the minimum speed at lower most position of the particle is √5gl to complete the circular motion.
Reason Work done by cnetripetal force on the particle is always zero.View SolutionQuestion 128
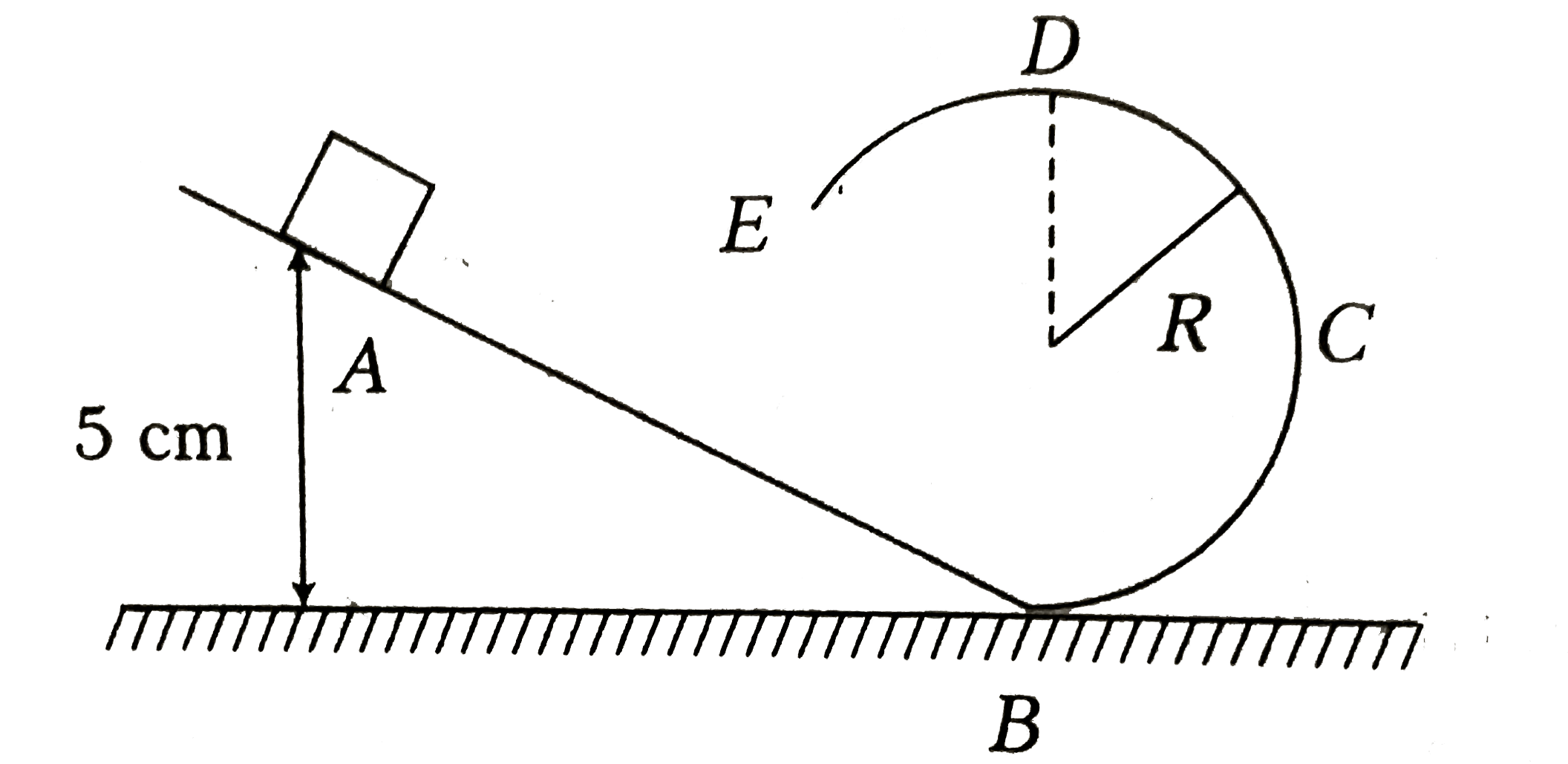
Assertion A car moves along a road with uniform speed. The path of car lies in vertical plane and shown in fighre. The radius of curvature (R) of the path is same everywhere. If the car does not loose contact with road at the highest point, it can travel the shown path without loosing contact with road anywhere else.
Reason For car to loose contact with road, the normal reaction between car and road should be zero.
 View Solution
View SolutionQuestion 135
A uniform circular disc of radius 50 cm at rest is free to turn about an axis which is perpendicualr to its plane and passes through its centre. It is subjected to a torque which produces a constant angular acceleration of 2rads−2. Its net acceleration in ms−2 the end of 2s is a approximatelyView SolutionQuestion 137
A particle of mass 10g moves along a circle of radius 6.4 cm with a constant tangential acceleration. What is the magnitude of this acceleration, if the kinetic energy of the particle becomes equal to 8×10−4J by the end of the second revolution after the begining of the motion?View Solution
All Exercises from DC PANDEY ENGLISH Class 11 PHYSICS CIRCULAR MOTION
- ASSERTION AND REASON
- CHECK POINT
- COMPREHENSION
- EXERCISE 10.1
- EXERCISE 10.2
- EXERCISE 10.3
- INTEGER
- JEE ADVANCED
- JEE MAIN
- LEVEL 1 OBJECTIVE
- LEVEL 1 SUBJECTIVE
- LEVEL 2 COMPREHENSION BASED
- LEVEL 2 MORE THAN ONE CORRECT
- LEVEL 2 SINGLE CORRECT
- LEVEL 2 SUBJECTIVE
- MATCH THE COLUMNS
- MATRIX MATCHING
- MEDICAL ENTRANCES S GALLERY
- MORE THAN ONE OPTION IS CORRECT
- SUBJECTIVE QUESTIONS
- TAKING IT TOGETHER
- EXAMPLE
- MISCELLANEOUS EXAMPLES
- SOLVED EXAMPLES