A sphere is suspended by a thread of length l. What minimum horizontal velocity has to be imparted to the ball for it to reach the height of the suspension?
√5 gl
2 gl
√gl
√2gl
The correct Answer is:D
To solve the problem of finding the minimum horizontal velocity that must be imparted to a sphere suspended by a thread of length l for it to reach the height of suspension, we will use the principle of conservation of mechanical energy.
1. Identify the Initial and Final States:
- The initial state (point A) is when the sphere is at the lowest point of its swing, and we will consider this point as our reference level for potential energy, where UA=0.
- The final state (point B) is when the sphere reaches the height of suspension (point O), where its potential energy will be maximum and kinetic energy will be minimum.
2. Apply Conservation of Mechanical Energy:
- According to the conservation of mechanical energy:
UA+KA=UB+KB
- At point A:
- Potential Energy UA=0
- Kinetic Energy KA=12mu2 (where u is the initial horizontal velocity imparted)
- At point B:
- Potential Energy UB=mgh (where h=l, the height of suspension)
- Kinetic Energy KB=0 (since we want to find the minimum velocity at the highest point, where the speed is momentarily zero)
3. Set Up the Equation:
- Substitute the energies into the conservation equation:
0+12mu2=mgl+0
- This simplifies to:
12mu2=mgl
4. Solve for u2:
- Cancel m from both sides (assuming m≠0):
12u2=gl
- Multiply both sides by 2:
u2=2gl
5. Find u:
- Taking the square root of both sides gives:
u=√2gl
Final Answer:
The minimum horizontal velocity that must be imparted to the sphere is:
u=√2gl
- The initial state (point A) is when the sphere is at the lowest point of its swing, and we will consider this point as our reference level for potential energy, where UA=0.
- The final state (point B) is when the sphere reaches the height of suspension (point O), where its potential energy will be maximum and kinetic energy will be minimum.
- According to the conservation of mechanical energy:
UA+KA=UB+KB
- At point A:
- Potential Energy UA=0
- Kinetic Energy KA=12mu2 (where u is the initial horizontal velocity imparted)
- At point B:
- Potential Energy UB=mgh (where h=l, the height of suspension)
- Kinetic Energy KB=0 (since we want to find the minimum velocity at the highest point, where the speed is momentarily zero)
- Substitute the energies into the conservation equation:
0+12mu2=mgl+0
- This simplifies to:
12mu2=mgl
- Cancel m from both sides (assuming m≠0):
12u2=gl
- Multiply both sides by 2:
u2=2gl
- Taking the square root of both sides gives:
u=√2gl
The minimum horizontal velocity that must be imparted to the sphere is:
u=√2gl
Topper's Solved these Questions
- CIRCULAR MOTIONBook:DC PANDEY ENGLISHChapter:CIRCULAR MOTIONExercise:Match the columns
Explore 3 Videos
- CIRCULAR MOTIONBook:DC PANDEY ENGLISHChapter:CIRCULAR MOTIONExercise:Medical entrances s gallery
Explore 19 Videos
- CIRCULAR MOTIONBook:DC PANDEY ENGLISHChapter:CIRCULAR MOTIONExercise:Check point
Explore 45 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBook:DC PANDEY ENGLISHChapter:CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONExercise:Level 2 Subjective
Explore 21 Videos
- COMMUNICATION SYSTEMBook:DC PANDEY ENGLISHChapter:COMMUNICATION SYSTEMExercise:Only One Option is Correct
Explore 27 Videos
Similar Questions
A small ball of mass 2×10−3kg, having a charge 1μC, is suspended by a string of length 0.8m. Another identical ball having the same charge is kept at the point of suspension. Determine the minimum horizontal velocity that should be imparted to the lower ball so that it can make a complete revolution.
View SolutionA bob of mass M is suspended by a massless string of length L. The horizontal velocity v at position A is just sufficient to make it reach the point B. The angle θ at which the speed of the bob is half of that at A, satisfies
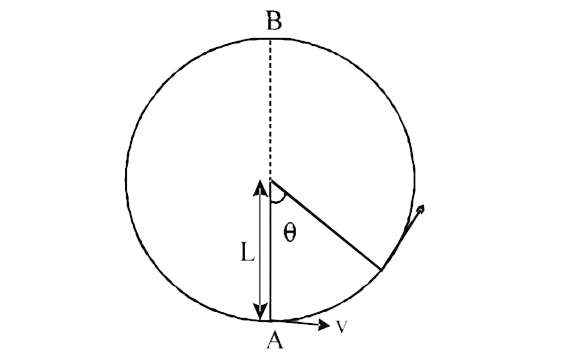
View Solution
Knowledge Check
A bob of mass m, suspended by a string of length l1 is given a minimum velocity required to complete a full circle in the vertical plane. At the highest point, it collides elastically with another bob of mass m suspended by a string of length l2, which is initially at rest. Both the strings are mass-less and inextensible. If the second bob, after collision acquires the minimum speed required to complete a full circle in the vertical plane, the ratio l1l2 is
A1B3C5D1/5
A heavy particle is suspended by a stirng of length l. The particle is given a horizontal velocity v0. The stirng becomes slack at some angle and the particle proceeds on a parabola.find the value of v0 if the prticle psses through the ponit of suspension
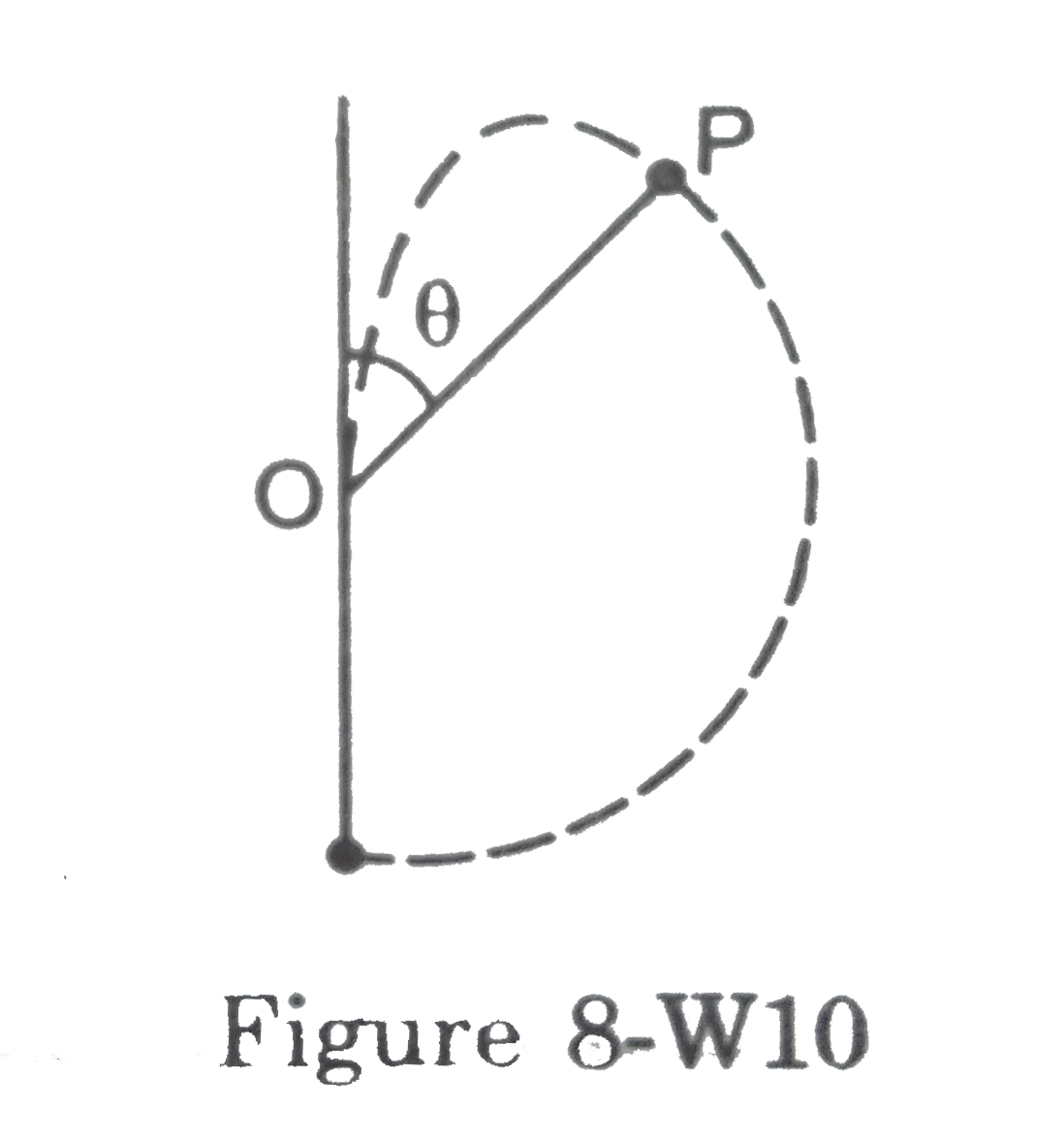
View SolutionIn all the four situations depicted in Column-I, a ball of mass m is connected to a string. In each case, find the tension in the string and match the appropriate entries in Column-II.
(A)(##VMCPHYXIWORBOK01_C04E03050_Q01##)Conical pendulum(P)T=mgcosθ(B)(##VMCPHYXIWORBOK01_C04E03050_Q02##)Pendulum is swinging. Angular position is the extreme position.T is tension in extreme position(Q)Tcosθ=mg(C)(##VMCPHYXIWORBOK01_C04E03050_Q03##)The car is moving with constant acceleration.The ball is at rest with respect to car(R)Speed of ball with respect to ground is constant(D)(##VMCPHYXIWORBOK01_C04E03050_Q04##)The car is moving with constant velocity. The ball is at rest with respect to car(S)Velocity of ball with respect to ground is changing continuously
View SolutionA light rod of length l is pivoted at the upper end. Two masses (each m), are attached to the rod, one at the middle and the other at the free end. What horizontal velocity must be imparted to the lower end mass, so that the rod may just take up the horizontal position ?
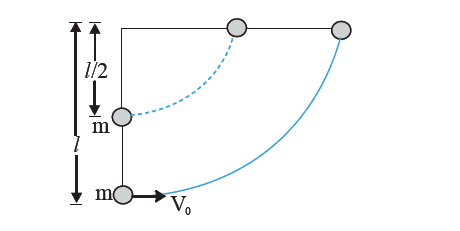
View SolutionA bob of mass m, suspended by a string of length l1 is given a minimum velocity required to complete a full circle in the vertical plane. At the highest point, it collides elastically with another bob of mass m suspended by a string of length l2, which is initially at rest. Both the strings are mass-less and inextensible. If the second bob, after collision acquires the minimum speed required to complete a full circle in the vertical plane, the ratio l1l2 is
View SolutionAn isolated charge q1 of mass m is suspended freely by a thread of length l. Another charge q2 is brought near it (r>>l). When q1 is in equilibrium tension in thread will be
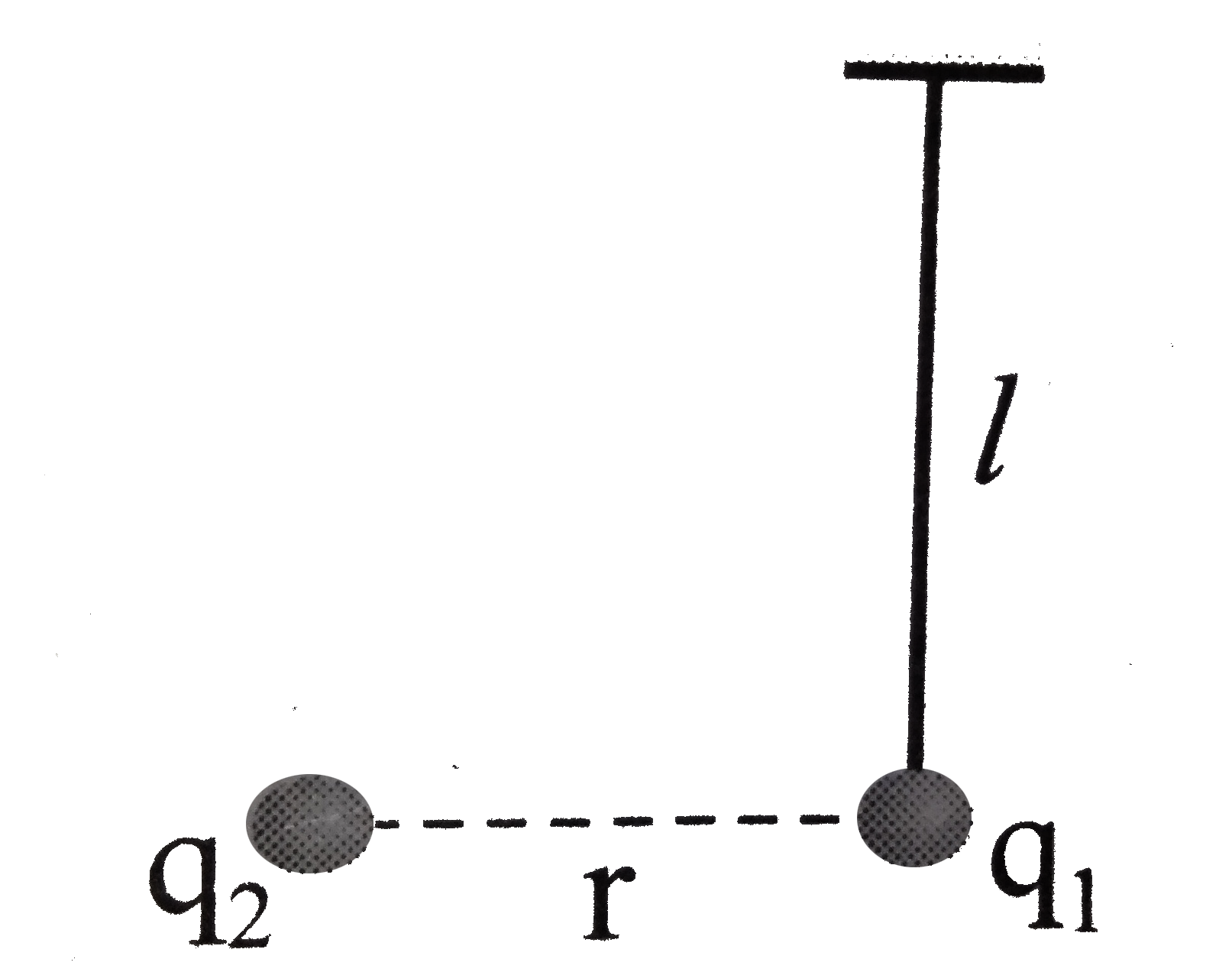
View SolutionA ball of mass m is attached to one end of a light rod of length l, the other end of which is hinged. What minimum velocity v should be imparted to the ball downwards, so that it can complete the circle ?

View SolutionA particle of mass m is suspended by a string of length l from a fixed rigid support. A sufficient horizontal velocity =√3gl is imparted to it suddenly. Calculate the angle made by the string with the vertical when the accekleration of the particle is inclined to the string by 45∘ .
View Solution